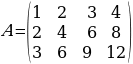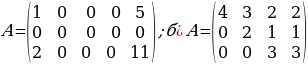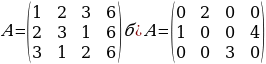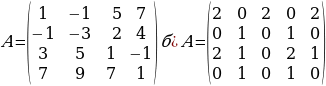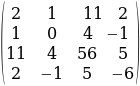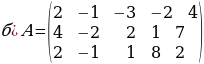Тема: Матрицанын рангы
Матрицанын рангы
Матрицанын рангын табуу усулдары
Матрицанын рангынын касиеттери
1.Матрицанын рангы
Матрицанын ж.б илимдердин маселелерин изилдөөдө жана чыгарууда матрицанын рангы деген түшүнүк негизги мааниге ээ.
Аныктама1.1:Берилген А матрицанын рангы деп бул матрицанын нөлдөн айырмалуу болгон минорлорунун эң жогорку тартибин айтабыз.
Аныктаманы башкачараак берүүгө да болот:
Аныктама1.1*:Матрицанын k-тартиптеги минору нөлдөн айырмалуу болуп , каалагандай (k+1)-тартиптеги минору нөлгө барабар болсо, анда k оң бүтүн саны матрицанын рангы деп аталат.
Эгерде матрицанын бардык элементтери нөлгө барабар болсо , андай матрицанын рангы нөлгө барабар болот.
Матрица А нын рангы же rang A же r (А) аркылуу белгиленет.
Аныктамадан төмөнкүлөрдү алабыз:
Берилген m x n - өлчөмдүү А матрицанын рангы r(A) ;
r(A)=0 качан гана А матрицанын бардык элементтери нөлгө барабар болсо.
Квадраттык n- тартиптеги А матрицанын рангы r(A)=n качан гана А -кубулбаган матрица болсо.
1-мисал:
A=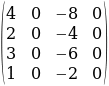
матрицанын рангын эсептөө
ЧЫГАРУУ: Матрица А 4-тартиптеги матрица болгондуктан
г(A) ≤4. Бирок detA = 0, себеби матрица А нөлдүк мамычаны кармайт. Демек, г(А) ≤3. Бул матрицанын 3 тартиптеги бардык айрым матрицалары да нөлдүк мамычаны кармагандыктан ал матрицалардын аныктагычтары нөлгө барабар. Демек, г(А) ≤2. Ал эми 2-тартиптеги бардык айрым матрицалары же нөлдүк мамычаны кармайт (экинчи же төртүнчү мамычалар) же пропорционалдуу мамычаларды кармайт (биринчи жана үчүнчү мамычалар). Демек, ал матрицалардын да аныктагычтары нөлгө барабар. Мындан r(A) ≤ 1 болот. Бирок матрица А нөл эмес элементтерди кармагандыктан, r(A) = 1 болот.
2-мисал:
A=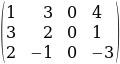
матрицанын рангын эсептөө
ЧЫГАРУУ: Бул матрица 3 х 4-өлчөмдүү болгондуктан, r(A) ≤ min(3; 4) = 3. Ранг 3 кө барабар болор болбосун текшеребиз. Ал үчүн А матрицанын бардык 3-тартиптеги минорлорун эсептейбиз (алар А матрицанын кандайдыр бир мамычасын сызып салуу аркылуу алынган айрым матрицанын аныктагычтары болот. Алардын саны төрт болот):

Бардык 3-тартиптеги минорлору нөл болгондуктан r(A)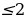 .
.
Бирок 2-тартиптеги нөлгө барабар болгон минор бар, мисалы,
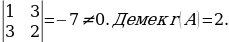
Жалпы учурда матрицанын рангын бардык минорлорду эсептөө аркылуу табуу көп эсептөөлөрдү талап кылат. Бул эсептөөлөрдү жеңилдетүү үчүн, матрицанын рангын сактаган элементардык өзгөртүүлөр колдонулат. Ал элементардык өзгөртүүлөргө төмөнкү өзгөртүүлөр кирет:
1. Нөлдүк жолчону (же мамычаны) алып салуу
2. Матрицанын кандайдыр бир жолчосунун (мамычасынын) бардык элементтерин нөл эмес санга көбөйтүү.
3. Матрицанын жолчолорунун (мамычаларынын) ордун алмаштыруу.
4. Матрицанын жолчосуна (мамычасына), каалаган санга көбөйтүлгөн башка жолчону (мамычаны) элементтеринин жайланыш ордуна карата кошуу.
5. Матрицаны транспозициялоо.
Эгерде r(A)=r(B) болсо, анда А жана В матрицалары эквиваленттүү деп аталышат жана A B деп белгиленет.
B деп белгиленет.
ТЕОРЕМА 1: Матрицага элементардык өзгөртүүлөрдү жүргүзсөк, анын рангы өзгөрбөйт.
ДАЛИЛДӨӨ:Аныктагычтын касиеттеринин негизинде квадраттык матрицага элементардык өзгөртүүлөрдү жүргүзсөк, анын аныктагычы өзгөрбөйт же нөл эмес санга көбөйтүлүп калат. Демек берилген матрицанын нөл эмес минорлорунун эң жогорку тартиби сакталат б.а. матрицанын рангы сакталат.
Элементардык өзгөртүүлөрдүн жардамы менен матрицаны баскычтуу түргө алып келип, рангын оңой эле эсептөөгө болот.
Элементардык өзгөртүүлөрдүн жардамы менен матрицанын рангын эсептөөнүн алгоритмин төмөнкү мисалда көрсөтөбүз.
3-МИСАЛ.
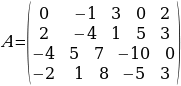
матрицанын рангын эсептөө.
ЧЫГАРУУ:1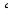 .Эгерде
.Эгерде 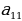 =0 болсо, анда жолчолорун же мамычаларын алмаштырып,
=0 болсо, анда жолчолорун же мамычаларын алмаштырып, 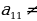 0 болгонго жетишебиз. Бул мисалда матрицанын 1- жана 2- жолчолорун алмаштырып
0 болгонго жетишебиз. Бул мисалда матрицанын 1- жана 2- жолчолорун алмаштырып 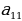 =2
=2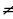 0 болгонго жетишебиз.
0 болгонго жетишебиз.
2°. Эгерде 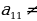 0 болсо, анда 1-жолчонун элементтерин
0 болсо, анда 1-жолчонун элементтерин 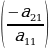 санына көбөйтүп 2- жолчого кошуп,
санына көбөйтүп 2- жолчого кошуп,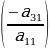 санына көбөйтүп 3- жолчого кошуп,
санына көбөйтүп 3- жолчого кошуп, 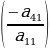 санына көбөйтүп 4-жолчого кошуп, 1-мамычанын
санына көбөйтүп 4-жолчого кошуп, 1-мамычанын 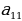 элементинен башка элементтери нөлгө барабар болгонуна жетишебиз:
элементинен башка элементтери нөлгө барабар болгонуна жетишебиз:
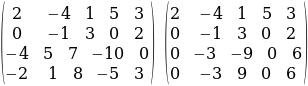
3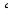 .Эгерде алынган матрицада
.Эгерде алынган матрицада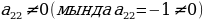 болсо , анда 2-жолчонун элементтерин
болсо , анда 2-жолчонун элементтерин 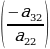 санына көбөйтүп 3-жолчого кошуп ,
санына көбөйтүп 3-жолчого кошуп , 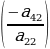 санына көбөйтүп 4-жолчого кошуп, 2-мамычанын
санына көбөйтүп 4-жолчого кошуп, 2-мамычанын 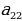 элементинен, төмөн жайланышкан элементтери нөл болгонго жетишебиз. Эгерде өзгөртүүдөн кийин нөлдөн жолчолор (же мамычалар) пайда болсо, анда ал нөлдүк жолчолорду (же мамычаларды) алып салабыз. Биздин мисалда:
элементинен, төмөн жайланышкан элементтери нөл болгонго жетишебиз. Эгерде өзгөртүүдөн кийин нөлдөн жолчолор (же мамычалар) пайда болсо, анда ал нөлдүк жолчолорду (же мамычаларды) алып салабыз. Биздин мисалда:
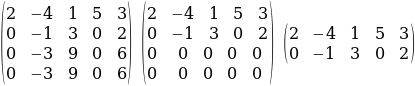
Акыркы матрица баскычтуу матрица жана ал матрица нөлгө барабар эмес 2-тартиптеги минорго ээ. Мисалы 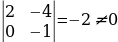
Мындан акыркы баскычтуу матрицанын, демек берилген матрицанын рангы 2 ге барабар, б.а. r(A) = 2.
2.Матрицанын рангын табуу усулдары
 Минорлордун жардамында матрицанын рангын табуу
Минорлордун жардамында матрицанын рангын табуу
Матрицадан нөлдөн айырмалуу k-тартиптеги М минору табылсын. Анда М минорун өзүнө камтыган (k+1) тартиптеги минорлорду карайбыз. Эгерде алардын баары нөлгө барабар болсо, анда матрицанын рангы k га барабар болот. Б. а. г(A)=k.
Тескери учурда, эгерде (k+1)- тартиптеги минор нөлдөн айырмалуу болсо, анда (k+2)- тартиптеги минорду изилдейбиз жана жогорудагы аракет кайталанат.
1-МИСАЛ:
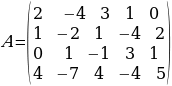
матрицанын рангын тапкыла.
Чыгаруу. 2-тартиптеги 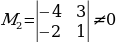 минорун табабыз. Бул минорду өзүнө кармаган
минорун табабыз. Бул минорду өзүнө кармаган 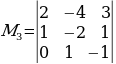 минорунун мааниси да нөлдөн айырмалуу болот. Бирок , 3-тартиптеги минорду кармаган
минорунун мааниси да нөлдөн айырмалуу болот. Бирок , 3-тартиптеги минорду кармаган 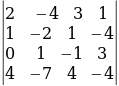 жана
жана 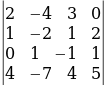 минорлорунун маанилери нөлгө барабар. Демек, r(A)=3.
минорлорунун маанилери нөлгө барабар. Демек, r(A)=3.
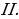 Элементардык өзгөртүп түзүүлөрдүн жардамында матрицанын рангын табуу
Элементардык өзгөртүп түзүүлөрдүн жардамында матрицанын рангын табуу
Бул усул матрицанын рангы элементардык өзгөртүп түзүүдөн өзгөрбөстүгүнө (теоремага) негизделген. Элементардык өзгөртүп түзүүлөрдүн жардамында матрицаны үч бурчтук көрүнүшүнө алып келебиз. Анда, ал матрицанын жолчолорунун саны матрицанын рангына барабар болот.
2-МИСАЛ:
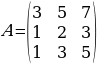
матрицанын рангын тапкыла.
ЧЫГАРУУ: Берилген матрицанын рангын табуу үчүн матрицага төмөнкүдөй элементардык өзгөртүп түзүүлөрдү жүргүзөбүз:
1.Матрицанын 1-жолчосунун жана 3-жолчосунун тиешелүү элементтерин кошобуз:
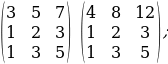
2.Биринчи жолчонун элементтерин 4 кө бөлөбүз:
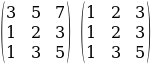 ;
;
3.Экинчи жолчонун элементтеринен 1-жолчонун тиешелүү элементтерин кемитебиз:
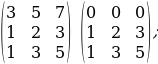
4.Матрицанын 1-жолчосун сызып таштайбыз:
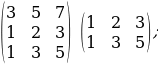
Демек, r(A)=2
Жообу: r(A)=2.
3.Матрицанын рангынын касиеттери
Матрицанын рангы төмөнкү касиеттерге ээ:
1. r (A+B) ≤r(A) + r (B)
2. r (A+B) ≥/r (A)-r (B) /
3. r(AB) ≤min 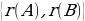
4. r(AA) = r(A)
5. г(АВ) = г (А), мында В-квадраттык матрица жана detB ≠ 0;
6. r(AB)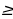 r(A) + г(В)-n, мында n-А матрицанын мамычаларынын же В матрицанын жолчолорунун саны.
r(A) + г(В)-n, мында n-А матрицанын мамычаларынын же В матрицанын жолчолорунун саны.
КӨНҮГҮҮЛӨР:
а) A=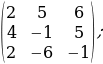 б) A=
б) A=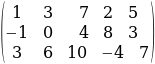
а) 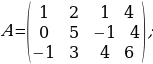 б)
б)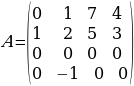
а) 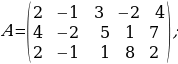 б)
б) 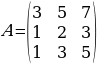
а) 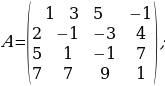 б)
б)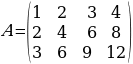
а) 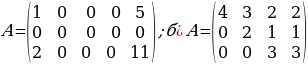
а) 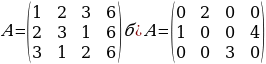
а) 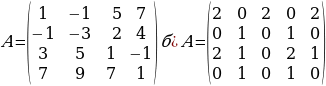
а) A=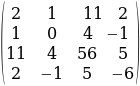
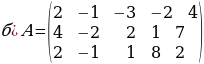
Колдонулган адабияттар:
1. Авыт Асанов , Рамиз Рафатов “Сызыктуу алгебра” 1.4 , 39-б , Бишкек – 2003.
2. Я.С Бугров, С.М Никольский. Элементы линейной алгебры и аналитическое геометрии М. Наука, 1984.






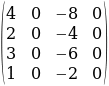
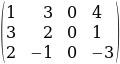

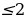 .
.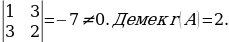
 B деп белгиленет.
B деп белгиленет.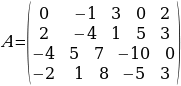
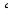 .Эгерде
.Эгерде 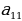 =0 болсо, анда жолчолорун же мамычаларын алмаштырып,
=0 болсо, анда жолчолорун же мамычаларын алмаштырып, 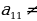 0 болгонго жетишебиз. Бул мисалда матрицанын 1- жана 2- жолчолорун алмаштырып
0 болгонго жетишебиз. Бул мисалда матрицанын 1- жана 2- жолчолорун алмаштырып 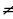 0 болгонго жетишебиз.
0 болгонго жетишебиз.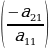 санына көбөйтүп 2- жолчого кошуп,
санына көбөйтүп 2- жолчого кошуп,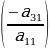 санына көбөйтүп 3- жолчого кошуп,
санына көбөйтүп 3- жолчого кошуп, 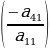 санына көбөйтүп 4-жолчого кошуп, 1-мамычанын
санына көбөйтүп 4-жолчого кошуп, 1-мамычанын 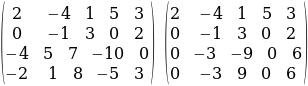
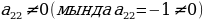 болсо , анда 2-жолчонун элементтерин
болсо , анда 2-жолчонун элементтерин 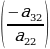 санына көбөйтүп 3-жолчого кошуп ,
санына көбөйтүп 3-жолчого кошуп , 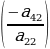 санына көбөйтүп 4-жолчого кошуп, 2-мамычанын
санына көбөйтүп 4-жолчого кошуп, 2-мамычанын 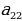 элементинен, төмөн жайланышкан элементтери нөл болгонго жетишебиз. Эгерде өзгөртүүдөн кийин нөлдөн жолчолор (же мамычалар) пайда болсо, анда ал нөлдүк жолчолорду (же мамычаларды) алып салабыз. Биздин мисалда:
элементинен, төмөн жайланышкан элементтери нөл болгонго жетишебиз. Эгерде өзгөртүүдөн кийин нөлдөн жолчолор (же мамычалар) пайда болсо, анда ал нөлдүк жолчолорду (же мамычаларды) алып салабыз. Биздин мисалда: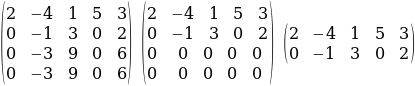
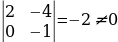
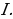 Минорлордун жардамында матрицанын рангын табуу
Минорлордун жардамында матрицанын рангын табуу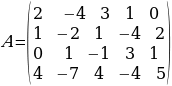
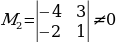 минорун табабыз. Бул минорду өзүнө кармаган
минорун табабыз. Бул минорду өзүнө кармаган 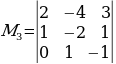 минорунун мааниси да нөлдөн айырмалуу болот. Бирок , 3-тартиптеги минорду кармаган
минорунун мааниси да нөлдөн айырмалуу болот. Бирок , 3-тартиптеги минорду кармаган 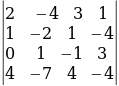 жана
жана 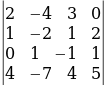 минорлорунун маанилери нөлгө барабар. Демек, r(A)=3.
минорлорунун маанилери нөлгө барабар. Демек, r(A)=3.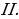 Элементардык өзгөртүп түзүүлөрдүн жардамында матрицанын рангын табуу
Элементардык өзгөртүп түзүүлөрдүн жардамында матрицанын рангын табуу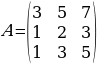
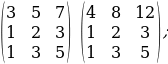
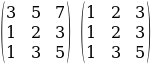 ;
;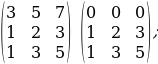
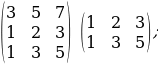
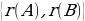
 r(A) + г(В)-n, мында n-А матрицанын мамычаларынын же В матрицанын жолчолорунун саны.
r(A) + г(В)-n, мында n-А матрицанын мамычаларынын же В матрицанын жолчолорунун саны.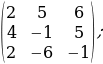 б) A=
б) A=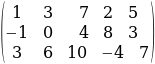
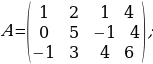 б)
б)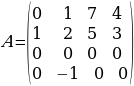
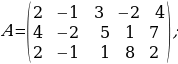 б)
б) 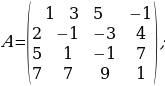 б)
б)