© 2020, Бекиева Малика Раимжановна 276


СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока

Тригонометриялык функциялар, тендемелер, барабарсыздыктар
Список вопросов теста
Вопрос 1
Кайсы функция жуп?
Варианты ответов
- y=sinx
- y=cosx
- y=tgx
- y=ctgx
Вопрос 2
y=sinx функциясынын графиги эмне деп аталат?
Варианты ответов
- гиперболла
- параболла
- синусоиада
- эллипс
Вопрос 3
y=cosx функциянын маанилеринин областын тап?
Варианты ответов
-
\(\left[-\infty;+\infty\right]\)
-
\(\left[-1;1\right]\)
-
\(\left[0;\pi\right]\)
-
\(\left(-\infty;+\infty\right)\)
Вопрос 4
Төмөндөгү график кайсы функцияга тиешелүү?
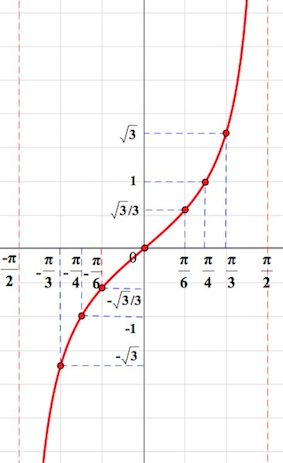
Варианты ответов
- синус
- косинус
- тангенс
Вопрос 5
\(\arcsin-\left(\frac{\sqrt{3}}{2}\right)\)
Варианты ответов
-
\(-\frac{\pi}{6}\)
-
\(-\frac{\pi}{3}\)
-
\(-\frac{\pi}{4}\)
-
0
Вопрос 6
a санынын арксинусу деп эмнени айтабыз?
Варианты ответов
-
\(\left[-\frac{\pi}{2};\frac{\pi}{2}\right]\) кесиндиден алынган синусу а га барабар болгон санды айтабыз
-
\(\left[-\frac{\pi}{2};\frac{\pi}{2}\right]\) кесиндиден алынган косинусу а га барабар болгон санды айтабыз
-
\(\left[-\pi;\pi\right]\) кесиндиден алынган синусу а га барабар болгон санды айтабыз
-
\(\left[0;\pi\right]\) кесиндисинен алынган синусу а га барабар болгон санды айтабыз
Вопрос 7
\(\cos x=\frac{1}{2}тендемеинин\ тамырын\ тапкыла\)
Варианты ответов
-
\(x=2\pi n,\ n\in Z\)
-
\(x=\pm\frac{\pi}{3}+2\pi n,\ n\in Z\)
-
\(x=\pm\frac{\pi}{6}+2\pi n,\ n\in Z\)
Вопрос 8
\(2\sin x+\sqrt{2}=0\ тендемесинин\ тамырын\ тап\)
Варианты ответов
-
\(x=\left(-1\right)^n\frac{\pi}{6}+2\pi n,\ n\in Z\)
-
\(x=\left(-1\right)^{n+1}\frac{\pi}{4}+2\pi n,\ n\in Z\)
-
\(x=\left(-1\right)^n\frac{\pi}{3}+2\pi n,\ n\in Z\)
-
\(x=2\pi n,\ n\in Z\)
Вопрос 9
\(3tgx+\sqrt{3}\ge0\ барабарсыздыкты\ чыгар\)
Варианты ответов
-
\(x\in\left(-\frac{\pi}{6}+\pi n;\frac{\pi}{2}+\pi n,n\in Z\right)\)
-
\(x\in\left[-\frac{2\pi}{3}+\pi n;\frac{\pi}{2}+\pi n\right]\)
-
\(x\in\left(-\frac{\pi}{2}+\pi n;\frac{\pi}{6}+\pi n,n\in Z\right)\)



