

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до 09.07.2025
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока

05.05.2020 р. 9 клас. Алгебра. Повторення. Функції. Властивості та графіки функцій у = kx+b, у = k/х, у = х2, у = корінь з х, у = aх2+bх+с
Лінійна функція — це функція, яку можна задати формулою y = kx+b, де x — незалежна змінна, k і b — деякі числа. Застосовуючи цю формулу, якщо відоме конкретне значення x, можна обчислити відповідне значення y. Нехай y = 0,5x−2. Тоді: якщо x = 0, тоді y =−2; якщо x = 2, тоді y = −1; якщо x = 4, тоді y = 0 і т. д. Зазвичай ці результати оформлюють у вигляді таблиці:
| x | 0 | 2 | 4 |
| y | −2 | −1 | 0 |
x - незалежна змінна (або аргумент), y - залежна змінна. Графіком лінійної функції y = kx+b є пряма. Щоб побудувати графік даної функції, нам достатньо мати координати двох точок, що належать графіку функції. Побудуємо на координатній площині xOy точки (0;−2) і (4;0), оформлені у таблиці, і проведемо через них пряму. 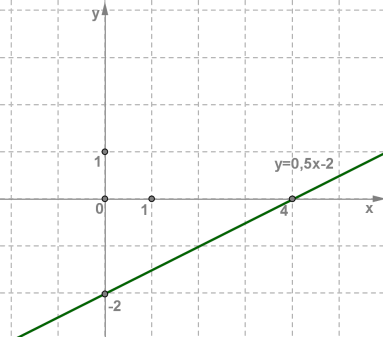 Багато реальних ситуацій описуються математичними моделями, що являють собою лінійні функції. Приклад: На складі було 500 т вугілля. Щодня почали підвозити 30 т вугілля. Скільки вугілля буде на складі через 2; 4; 10 днів? Якщо пройшло x днів, то кількість y вугілля на складі (у тоннах) можна виразити формулою y = 500+30x. Таким чином, лінійна функція y = 30x+500 є математичною моделлю ситуації. За x = 2 маємо y = 560; за x = 4 маємо y = 620; за x = 10 маємо y = 800. Однак треба враховувати, що в цій ситуації x∈N. (натуральне число) Якщо лінійну функцію y = kx+b треба розглядати не за всіх значень x, а лише для значень x із деякої числової множини X, то пишуть y = kx+b, x∈X. Приклад: Побудувати графік лінійної функції: a) y = −2x+1, x∈[−3;2]; б) y = −2x+1, x∈(−3;2). Складемо таблицю значень функції:
Багато реальних ситуацій описуються математичними моделями, що являють собою лінійні функції. Приклад: На складі було 500 т вугілля. Щодня почали підвозити 30 т вугілля. Скільки вугілля буде на складі через 2; 4; 10 днів? Якщо пройшло x днів, то кількість y вугілля на складі (у тоннах) можна виразити формулою y = 500+30x. Таким чином, лінійна функція y = 30x+500 є математичною моделлю ситуації. За x = 2 маємо y = 560; за x = 4 маємо y = 620; за x = 10 маємо y = 800. Однак треба враховувати, що в цій ситуації x∈N. (натуральне число) Якщо лінійну функцію y = kx+b треба розглядати не за всіх значень x, а лише для значень x із деякої числової множини X, то пишуть y = kx+b, x∈X. Приклад: Побудувати графік лінійної функції: a) y = −2x+1, x∈[−3;2]; б) y = −2x+1, x∈(−3;2). Складемо таблицю значень функції:
| x | −3 | 2 |
| y | 7 | −3 |
Позначимо на координатній площині xOy точки (−3;7) і (2;−3) та проведемо через них пряму. Далі виділимо відрізок, що з'єднує позначені точки. Цей відрізок і є графіком лінійної функції y=−2x+1,x∈[−3;2]. Точки (−3;7) і (2;−3) належать даному інтервалу (квадратні дужки) та на рисунку позначені темними кружечками. 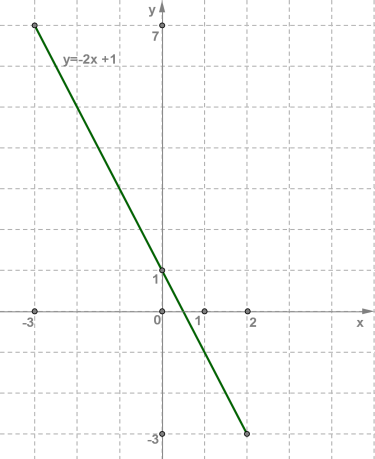 б) У другому випадку функція та сама, тільки значення x = −3 і x = 2 не розглядаються, оскільки вони не належать інтервалу (−3;2) (круглі дужки). Тому точки (−3;7) і (2;−3) на рисунку позначені світлими кружечками.
б) У другому випадку функція та сама, тільки значення x = −3 і x = 2 не розглядаються, оскільки вони не належать інтервалу (−3;2) (круглі дужки). Тому точки (−3;7) і (2;−3) на рисунку позначені світлими кружечками. 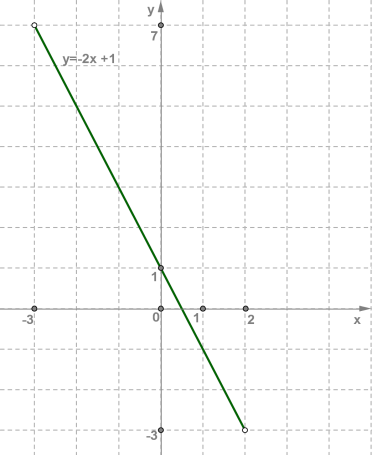 Розглядаючи графік лінійної функції на інтервалі, можна назвати найбільше і найменше значення лінійної функції. У випадку a) y = −2x+1, x∈[−3;2] маємо, що yнайб. = 7 і унайм. = −3, б) y = −2x+1, x∈(−3;2) маємо, що ні найбільшого, ні найменшого значень лінійної функції немає, оскільки обидва кінці відрізка, у яких саме й досягалися найбільше і найменше значення, виключені з розгляду. У ході побудови графіків лінійних функцій, можна ніби «підніматися вгору» або «спускатися з гірки», тобто лінійна функція або зростає, або спадає. Якщо k>0, тоді лінійна функція y = kx+b зростає; якщо k<0, тоді лінійна функція y = kx+b спадає.
Розглядаючи графік лінійної функції на інтервалі, можна назвати найбільше і найменше значення лінійної функції. У випадку a) y = −2x+1, x∈[−3;2] маємо, що yнайб. = 7 і унайм. = −3, б) y = −2x+1, x∈(−3;2) маємо, що ні найбільшого, ні найменшого значень лінійної функції немає, оскільки обидва кінці відрізка, у яких саме й досягалися найбільше і найменше значення, виключені з розгляду. У ході побудови графіків лінійних функцій, можна ніби «підніматися вгору» або «спускатися з гірки», тобто лінійна функція або зростає, або спадає. Якщо k>0, тоді лінійна функція y = kx+b зростає; якщо k<0, тоді лінійна функція y = kx+b спадає.
Розглянемо функцію y = 2/x та складемо таблицю значень цієї функції:
| x | 1 | 2 | −1 | −2 | 4 | 8 | −4 | −8 |
| y | 2 | 1 | −2 | −1 | ½ | ¼ | −½ | −¼ |
Побудуємо ці точки на координатній площині. Вони намічають деяку лінію, що складається з двох гілок. Проведемо її.

Графік даної функції є лінія, яка називається гіперболою.
Графік функції y = −f(x) симетричний графіку функції y = f(x) щодо осі x.
Взагалі, графіком функції y = k/x, k≠0 є гіпербола, гілки якої розташовані в першому і третьому координатних кутах, якщо k>0, і в другому та четвертому координатних кутах, якщо k<0.
Точка (0;0) — центр симетрії гіперболи.
Зазвичай кажуть, що дві величини x і y обернено пропорційні, якщо вони пов'язані співвідношенням xy = k (де k — число, відмінне від 0) або, що те ж саме, y = kx.
З цієї причини функцію y = k/x називають іноді оберненою пропорційністю (за аналогією з функцією y = kx, яку називають прямою пропорційністю).
Число k — коефіцієнт оберненої пропорційності.
Властивості функції y = kx, якщо k>0
Описуючи властивості цієї функції, ми будемо спиратися на її геометричну модель — гіперболу.

1. Область визначення функції складається зі всіх чисел, окрім x=0.
2. y>0, якщо x>0; y<0, якщо x<0.
3. Функція спадає на проміжках (−∞;0) і (0;+∞).
4. Функція необмежена ні знизу, ні зверху.
5. Функція не має ні найменшого, ні найбільшого значення.
6. Функція неперервна на проміжках (−∞;0) і (0;+∞) і зазнає розриву, якщо x = 0.
7. Область значень — об'єднання двох відкритих променів (−∞;0)∪(0;+∞).
Властивості функції y = k/x, якщо k<0
Описуючи властивості цієї функції, ми будемо спиратися на її геометричну модель — гіперболу.

1. Область визначення функції складається зі всіх чисел, окрім x=0.
2. y>0, якщо x<0; y<0, якщо x>0.
3. Функція зростає на проміжках (−∞;0) і (0;+∞).
4. Функція необмежена ні знизу, ні зверху.
5. Функція не має ні найменшого, ні найбільшого значення. 6. Функція неперервна на проміжках (−∞;0) і (0;+∞) і зазнає розриву, якщо x=0.
7. Область значень — об'єднання двох відкритих променів (−∞;0)∪(0;+∞).
Для побудови графіка функції y=√х надамо незалежній змінній x декілька конкретних значень (невід'ємних, оскільки якщо x<0, то вираз √х не має сенсу), а також обчислимо відповідні значення залежної змінної y.
Звісно, ми будемо надавати x такі значення, для яких точне значення квадратного кореня є відомим.
Отже: якщо x = 0, то y = √0 = 0; якщо x = 1, то y = √1=1; якщо x = 4, то y = √4 = 2; якщо x = 9, то y = √9 = 3.
У такий спосіб ми склали таблицю значень функції:
| x | 0 | 1 | 4 | 6,25 | 9 |
| y | 0 | 1 | 2 | 2,5 | 3 |
Побудуємо знайдені точки (0;0), (1;1), (4;2), (6.25;2.5), (9;3) на координатній площині.
Вони намічаються певною лінією, накреслимо її.

Ми отримали графік функції y = √х.
Зверни увагу!
Графік дотикається осі y в точці (0;0)
Зауважимо, що, маючи шаблон параболи y = x2, з його допомогою можна легко побудувати графік функції y=√х, адже це — вітка тієї ж параболи, тільки орієнтована не вгору, а вправо.
Властивості функції y = √х.
Описуючи властивості цієї функції, ми, як завжди, будемо спиратися на її геометричну модель — вітку параболи.
1. Область визначення функції — промінь [0;+∞)
2. y = 0, якщо x = 0; y>0, якщо x>0
3. Функція зростає на промені [0;+∞) 4. Функція обмежена знизу та необмежена зверху.
5. yнайм= 0 при x = 0; yнайб не існує
6. Функція неперервна на промені [0;+∞)
Функція у = х2 та її графік
Область визначення цієї функції — множина всіх дійсних чисел.
Область значень — множина всіх невід’ємних чисел.
Графіком функції є парабола. Парабола — це крива, яка має дві вітки, що з’єднуються в точці, яка називається вершиною параболи.
Графік перетинає вісь ординат у точці з абсцисою 0.
Графік дотикається до осі абсцис.
Графік функції розміщується в першій і другій координатних чвертях.
Графік функції симетричний відносно осі ординат.
При від’ємних значеннях змінної x функція спадна. При додатних значеннях змінної x функція зростаюча.
При нульовому значенні змінної x значення функції y дорівнює нулю: x = 0, y = 0.
Якщо значення аргументу є протилежними числами, то значення функції в цих точках дорівнюють одне одному.
Щоб побудувати графік функції у = х2, достатньо знайти значення функції при декількох додатних значеннях аргументу і х = 0; провести вітку параболи через одержані точки, після чого відобразити її симетрично відносно осі ординат.
Функція, яку можна задати формулою виду y = ax2 + bx + c, де a, b і с - деякі числа, причому а відмінне від нуля, x - незалежна змінна, називають квадратичною.
Побудуємо графік функції у = x2−2x−3.
1. Маємо: a = 1, b = −2, x0 = −b/2a = 1, y0 = у(1) = 12 −2 · 1 − 3 = −4. Отже, вершиною параболи є точка (1;−4), а віссю параболи — пряма x = 1.
2. Візьмемо на осі x дві точки, симетричні відносно осі параболи, наприклад, точки x = −1 та x = 3. Маємо у(−1) = у(3) = 0. Побудуємо на координатній площині точки (−1;0) та (3;0).
3. Через точки (−1;0),(1;−4),(3;0) проводимо параболу.

Коренями рівняння x2−2x−3=0 є абсциси точок перетину параболи з віссю х; отже, корені рівняння такі: x1 = −1; x2 = 3. -1 та 3 - нулі функції.
05.05.2020 р. Скласти конспект матеріалу. Виконати вправу № 20.42 (5 випадок - І варіант, 8 випадок - ІІ варіант).











