22.04.2020 р. 9 клас. Повторення. Геометрія. Трикутники. Види трикутників. Площа трикутника

Трикутником називають фігуру, яка складається з трьох точок, що не лежать на одній прямій, і трьох відрізків, які сполучають ці точки. Трикутники за видами їх кутів: гострокутний, прямокутний та тупокутний.

Класифікація трикутників за кількістю рівних сторін: рівнобедрений (дві сторони рівні), рівносторонній (усі сторони рівні) та різностронній (сторони мають різні довжини).

Такі трикутники мають особливі властивості.

Трикутник називається рівнобедреним, якщо в нього дві сторони рівні.

Дві рівні сторони рівнобедреного трикутника називають бічними сторонами, а третя сторона — основою.

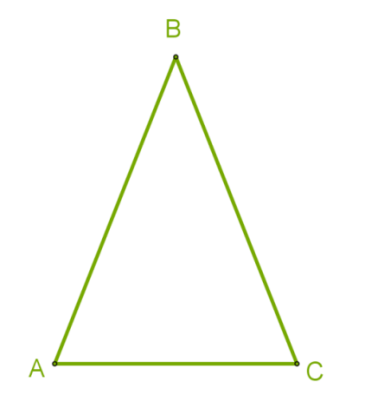
На рисунку зображено рівнобедрений трикутник ABC з бічними сторонами AB і BC та основою AC.

Трикутник називається рівностороннім, якщо в нього всі сторони рівні.

Зверни увагу!

Зазначимо, що рівносторонній трикутник також є рівнобедреним, причому будь-які дві його сторони можна вважати бічними.

Рівнобедрений трикутник має властивості, яких не мають різносторонні трикутники:

1. У рівнобедренному трикутнику кути, прилеглі до основи, є рівними.

2. У рівнобедренному трикутнику бісектриса, проведена до основи, є медіаною і висотою.

3. У рівнобедренному трикутнику медіана, проведена до основи, є бісектрисою і висотою.

Наслідок У рівносторонньому трикутнику всі кути рівні.

Ознака рівнобедреного трикутника Якщо в трикутнику два кути рівні, то він рівнобедрений.

Наслідок (ознака рівностороннього трикутника) Якщо в трикутнику всі кути рівні, то він рівносторонній.

Наслідок У рівносторонньому трикутнику медіана, бісектриса й висота, проведені з однієї вершини, збігаються.

Зверни увагу!

На практиці для розв’язування задач замість доведеної теореми часто використовують твердження про збіг лише двох із трьох зазначених відрізків: 1) якщо в трикутнику медіана й висота, проведені з однієї вершини, збігаються, то такий трикутник є рівнобедреним; 2) якщо в трикутнику бісектриса й висота, проведені з однієї вершини, збігаються, то такий трикутник є рівнобедреним; 3) якщо в трикутнику медіана й бісектриса, проведені з однієї вершини, збігаються, то такий трикутник є рівнобедреним.

Властивості прямокутного трикутника

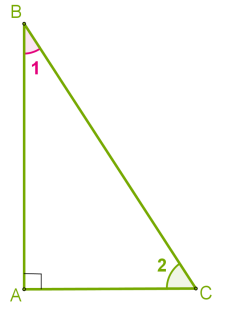
Прямокутний трикутник має один прямий і два гострі кути.

Сторона прямокутного трикутника, протилежна прямому куту, називається гіпотенузою, дві інші сторони — катетами.

На рисунку у трикутнику △ABC:

∠А=90°, BC — гіпотенуза, AC і AB — катети.

З теореми про суму кутів трикутника випливає:

сума гострих кутів прямокутного трикутника дорівнює 90°.

Справедливе також обернене твердження, що є ознакою прямокутного трикутника:

якщо в трикутнику сума двох кутів дорівнює 90°, то цей трикутник прямокутний.

∠ 1+ ∠ 2= 90°.

Ознаки рівності прямокутних трикутників

Користуючись ознаками рівності трикутників і теоремою про суму кутів трикутника, можна сформулювати ознаки рівності характерні тільки для прямокутних трикутників:

1. Ознака рівності прямокутних трикутників за двома катетами Якщо два катети одного прямокутного трикутника відповідно дорівнюють двом катетам другого прямокутного трикутника, то такі трикутники рівні.

2. Ознака рівності прямокутних трикутників за катетом і прилеглим гострим кутом Якщо катет і прилеглий до нього гострий кут одного прямокутного трикутника відповідно дорівнюють катету й прилеглому до нього гострому куту другого прямокутного трикутника, то такі трикутники рівні.

3. Ознака рівності прямокутних трикутників за катетом і протилежним кутом Якщо катет і протилежний йому кут одного прямокутного трикутника відповідно дорівнюють катету й протилежному йому куту другого прямокутного трикутника, то такі трикутники рівні.

4. Ознака рівності прямокутних трикутників за гіпотенузою й гострим кутом Якщо гіпотенуза й гострий кут одного прямокутного трикутника відповідно дорівнюють гіпотенузі й гострому куту другого прямокутного трикутника, то такі трикутники рівні.

5. Ознака рівності прямокутних трикутників за гіпотенузою й катетом Якщо гіпотенуза й катет одного прямокутного трикутника відповідно дорівнюють гіпотенузі й катету другого прямокутного трикутника, то такі трикутники рівні.

Прямокутний трикутник із кутом 30°

Катет прямокутного трикутника, що лежить навпроти кута 30°, дорівнює половині гіпотенузи (гіпотенуза удвічі довша від катета навпроти кута 30°).

Формул для обчислення площі трикутника в літературі можна знайти більше 10. Більшість з них можна застосувати в задачах з відомими сторонами та кутами трикутниками. Однак є ряд складних прикладів, в яких задано лише одна сторона і кути трикутника, або радіус описаного чи вписаного кіл та ще одна характеристика. В таких випадках просту формулу застосувати не вдасться. Задачі на трикутники вивчають в 7, 8 класі з вивчення простих властивостей, обчислення площі і периметра. В 9, 10 класі учні не тільки знають чим відрізняється прямокутний трикутник від рівнобедреного чи рівностороннього, а й з успіхом використовують теорему косинусів для знаходження сторін, формулу Герона, вміють розв'язати задачі про коло вписане або описане навколо трикутника. Але до всього потрібно приходити поступово не перевантажуючи пам'ять та можливості учнів. Тоді накопичені знання можна з успіхом застосувати до обчислення задач на трикутники будь-якої складності. Наведені нижче формули дозволять розв'язати 95 відсотків задач в яких потрібно знайти площу трикутника. Далі у формулах введені класичні позначення усіх його характеристик a,b,c – сторони трикутника, R– радіус описаного кола, r – радіус вписаного кола, ha,h_b,h_c висоти, проведені відповідно до сторін a,b,c. A, B, C – кути при вершинах.

Основні формули площі трикутника

1. Класична формула площі трикутника за відомою висотою та стороною

Площа трикутника рівна половині добутку сторони трикутника на висоту, опущену до цієї сторони.

2. Формула площі трикутника за двома сторонами a, b та кутом між ними С. S_{трик. =} ½ ab sin C.

3. Формула площі довільного трикутника за трьома сторонами a,b,c.

Формулу Герона застосовують в прикладах з відомими трьома сторонами трикутника. Спочатку знаходять півпериметр трикутника, як суму всіх його сторін розділену на два. S_трик. = квадратний корінь з добутку p(p - a)(p - b)(p - c).

4. Площа трикутника за трьома сторонами та радіусом описаного кола

У прикладах де задано три сторони і радіус (діаметр) описаного кола площу знаходять за формулою. S = abc/4R.

5. Формула площі за радіусом вписаного в трикутник кола та трьома сторнами

Якщо крім трьох сторін трикутника (периметра, півпериметра) відомий ще радіус вписаного кола, то площа обчислюється за формулою: площа трикутника дорівнює добутку його півпериметра та радіуса вписаного кола. S = pr

В добавку розглянемо – часткові випадки: Площа прямокутного трикутника з катетами a і b рівна половині їх добутку

Формула площі рівностороннього (правильного) трикутника:

рівна одній четвертій добутку квадрату сторони на корінь з трійки.

Задача. Сторони трикутника рівні 3, 5, 6 см. Знайти площу трикутника.

Розв'язання. Застосуємо формулу Герона, для цього спочатку знайдемо півпериметр p=(a+b+c)/2=(3+4+5)/2=7 (см). За формулою Герона обчислюємо площу трикутника. Відповідь: ≈ 7,48 см².

Скласти конспект теоретичного матеріалу. Виконати вправу. Дві сторони трикутника дорівнюють 5 см і 8 см, а кут між ними - 60^о. Знайдіть радіус кола, описаного навколо даного трикутника.