, Ленинградская область
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до 18.06.2025
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 06.05.2025 22:49
Духовская Надежда Олеговна
учитель
62 года
1 876
32 594 
Местоположение
Специализация
Треугольник Пенроуза
На внеклассных заниятиях по математике я люблю обращать внимание на " невозможные фигуры ". Это касается Треугольника Пенроуза, "Чертовой вилки", гравюр Мариуса Эшера. Для детей я подготовила презентацию ( https://multiurok.ru/files/treugolnik-penrouza.html ). Занятно выполнить модель этой фигуры.
Расхожее выражение "обман зрения" по сути своей неверно. Глаза не могут обмануть нас, поскольку являются только промежуточным звеном между объектом и мозгом человека. Обман зрения обычно возникает не из-за того, что мы видим, а из-за того, что бессознательно рассуждаем и невольно заблуждаемся: "посредством глаза, а не глазом смотреть на мир умеет разум".
Одним из наиболее эффектных направлений художественного течения является , основанный на изображении невозможных фигур. Невозможные объекты представляют собой рисунки на плоскости (любая плоскость двухмерна), изображающие трехмерные структуры, существование которых в реальном трехмерном мире невозможно. Классической и одной из самых простых фигур является невозможный треугольник.
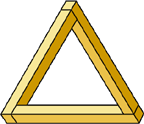
В невозможном треугольнике каждый угол сам по себе является возможным, но парадокс возникает, когда мы рассматриваем его целиком. Стороны треугольника направлены одновременно и к зрителю, и от него, поэтому отдельные его части не могут образовать реальный трехмерный объект.
 |
 |
|
| Невозможный треугольник Пенроуза | Треугольник, воспринимаемый как "возможный" |
Собственно говоря, наш мозг интерпретирует рисунок на плоскости как трехмерную модель. Сознание задает "глубину", на которой находится каждая точка изображения. Наши представления о реальном мире сталкиваются с противоречием, с некоей непоследовательностью, и приходится делать некоторые допущения:
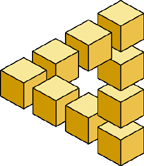Треугольник
Рейтерсвэрда |
- прямые двухмерные линии интерпретируются как прямые трехмерные линии;
- двухмерные параллельные линии интерпретируются как трехмерные параллельные линии;
- острые и тупые углы интерпретируются как прямые углы в перспективе;
- внешние линии рассматриваются как граница формы. Эта внешняя граница чрезвычайно важна для построения полного изображения.
Человеческое сознание сначала создает общее изображение предмета, а затем рассматривает отдельные части. Каждый угол совместим с пространственной перспективой, но, воссоединившись, они образуют пространственный парадокс. Если закрыть любой из углов треугольника, то невозможность пропадает.
07.01.2022 16:20
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
Полезное для учителя
Реализация образовательных программ осуществляется с применением исключительно электронного обучения и ДОТ
