2 Система сходящихся сил

• ГПОУ «Читинский техникум отраслевых технологий и бизнеса»

Презентация по технической механике

на тему « Плоская система сходящихся сил »

Разработал: преподаватель Батуев Б. Н.

Чита - 2015

ПЛОСКАЯ СИСТЕМА СХОДЯЩИХСЯ СИЛ- линии действия которых лежат в одной плоскости и все пересекаются в одной точке.

Плоская система сходящихся сил эквивалентна равнодействующей, которая равна векторной сумме этих сил; линия действия равнодействующей проходит через точку пересечения линий действия составляющих.

Построение, выполненное на рис. а, можно заменить более простым (рис. б).

Многоугольник АВСD называется силовым многоугольником.

• Способы определения равнодействующей:
• геометрический ( с помощью геометрии, тригонометрии),
• графический (с помощью чертежа в масштабе. Равнодей-ствующая определится измере-нием замыкающей стороны и умножением на масштаб.

Геометрическое условие равнове-сия плоской системы сходящихся сил

• F ∑ = F 1 + F 2 + F 3 + … + F n = ∑F i = 0
• Для равновесия необходимо и достаточно, чтобы силовой многоугольник был замкнут.
• Условия равновесия в виде равенств с неизвестными называются уравнениями равновесия.

• Этапы решения задачи статики :
• 1) Выбор тела для равновесия;
• 2) Отбрасывание связи и замена реак-циями.
• 3) Установление системы сил, дейст-вующих на тело;
• 4) Используя условия равновесия, на-хождение неизвестных.
• При решении задач размерности, единицы величин слагаемых и обеих частей уравнения должны быть одинаковыми.

Проекции силы на оси координат

•   В тех случаях, когда на тело действует более трех сил, а также когда неизвестны направления некоторых сил, удобнее при решении задач пользоваться не геометрическим, а аналитическим условием равновесия, которое основано на методе проекций.
• - отрезок оси, заключенный между двумя перпендикулярами, опущенными на ось из начала и конца вектора силы.

• Пусть даны координатные оси х, у, сила Р, приложенная в точке А и расположенная в плоскости координатных осей (рис.).
• Проекциями силы Р на оси будут отрезки аЬ и а'b'. Обозначим эти проекции соответственно Р х и Р у . Тогда
• Px = P cos α; Py = P sin α.
• Проекция силы на ось есть величина алгебраическая, которая может быть положительной или отрицательной, что устанавливается по направлению проекции. За направление проекции примем направление от проекции начала к проекции конца вектора силы.

• правило знаков: если направление проекции силы на ось совпадает с положительным направлением оси, то эта проекция считается (+), и наоборот.
• Если вектор силы // оси, то он проецируется на эту ось в натуральную величину (сила F).
• Если вектор силы перпендикулярен оси, то его проекция на эту ось равна 0 (сила Q).

• Зная две проекции Р х и Р у , из треугольника A ВС определяем модуль и направление вектора силы Р по следующей формуле:
• модуль силы
• P = √(Px² + Py²),

Аналитический (математический) способ определения равнодействующей плоской системы сходящихся сил

• Пусть дана плоская система n сходящихся сил
• F1, F2, F3, …, Fn.
• Равнодействующая этой системы
• F∑ = ∑Fi.
• В плоскости действия данной системы выберем ось координат и спроецируем данные силы и их равнодействующую на эту ось.
•  

Из математики известно свойство проекции векторной суммы, на основании которого можно утверждать, что проекция равнодействующей на ось равна алгебраической сумме проекций составляющих сил на ту же ось, т. е.

F ∑ x = ∑F ix .

•   Правую часть этого равенства записываем упрощенно, а именно:

F ∑ x = ∑x.

•   Для того чтобы определить равнодействующую любой плоской системы сходящихся сил, спроецируем их на оси координат х и у, алгебраически сложим проекции всех сил и найдем, таким образом, проекции равнодействующей:

F ∑ x = ∑x, F ∑ y = ∑y.

• Зная проекции, на основании формул, определим модуль и направление равнодействующей: модуль равнодействующей

F ∑ = √F ∑ x² + F ∑ y² ;

•   направляющий тангенс угла между вектором F ∑ и осью х

tg (F ∑ , x ) = F ∑ y / F ∑ x .

• Линия действия равнодействующей проходит через точку пересечения линий действия составляющих сил.

Аналитические условия равновесия плоской системы сходящихся сил

•   Если данная плоская система сходящихся сил находится в равновесии, то равнодействующая такой системы, а значит, и проекции равнодействующей на оси координат равны нулю:
• F∑ = 0, F∑x = 0, F∑y = 0.
• Учитывая, что F∑x = ∑x , F∑y = ∑y ,
• получаем равенства, выражающие аналитические условия равновесия плоской системы сходящихся сил: ∑x = 0, ∑y = 0.
• Формулируются эти условия следующим образом: для равновесия плоской системы сходящихся сил необходимо и достаточно, чтобы алгебраическая сумма проекций этих сил на каждую из двух координатных осей равнялась нулю.

С помощью уравнений равновесия можно определить два неизвестных элемента данной системы сил, например модуль и направление одной силы или модули двух сил, направления которых известны, и т. п.

• Выведенные условия равновесия справедливы для любых осей координат, но для упрощения решения задач рекомендуется оси координат выбирать по возможности перпендикулярными неизвестным силам, чтобы каждое уравнение равновесия содер­жало одно неизвестное.
• Когда направление искомой силы неизвестно, ее можно разложить на две составляющие по заданным направлениям, обычно по направлениям координатных осей; по найденным двум взаимно перпендикулярным составляющим легко опреде­ляется неизвестная сила.
• Если при решении задач аналитическим способом искомая реакция получится отрицательной, то это значит, что действительное ее направление противоположно направлению, принятому на рисунке.

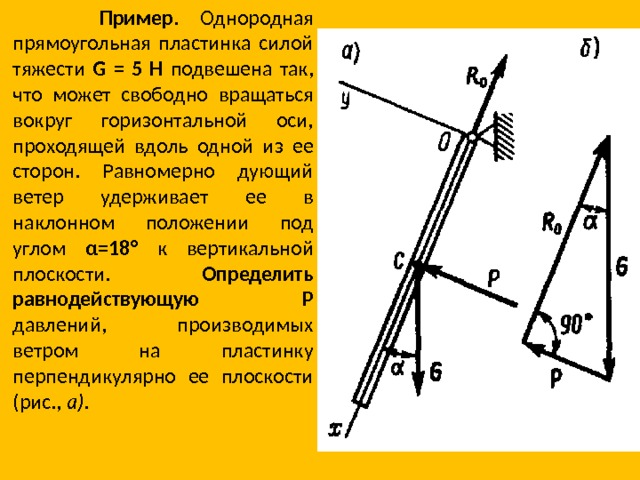
• Пример . Однородная прямоугольная пластинка силой тяжести G = 5 Н подвешена так, что может свободно вращаться вокруг горизонтальной оси, проходящей вдоль одной из ее сторон. Равномерно дующий ветер удерживает ее в наклонном положении под углом α=18° к вертикальной плоскости. Определить равнодействующую Р давлений, производимых ветром на пластинку перпендикулярно ее плоскости (рис., а).

• Решение. Рассмотрим равновесие пластинки. Отбросим шарнир О. Так как пластинка однородная и прямоугольной формы, то равнодействующая Р давлений ветра и сила тяжести G пересекаются в геометрическом центре С пластинки; линия действия реакции R 0 шарнира на основании теоремы о равновесии трех непараллельных сил также пройдет через точку С. Для системы трех сходящихся сил, действующих на пластинку, применимо аналитическое условие равновесия ∑У=0, направив ось у перпендикулярно пластинке (чтобы реакция R 0 , которую не требуется определять, не вошла в уравнение равновесия). Составим уравнение равновесия
• ∑ У=0; P – G sin α = 0,
• откуда
• P = G sin α = 5 · 0,309 ≈ 1,55 Н.
• Проведем проверку решения задачи с помощью геометрического условия равновесия:
• ∑ Fi = 0; G + P + R0 = 0.
• Построим замкнутый силовой треугольник (рис., б). Решая его, получим P = G· sin α = 5 sin 18°≈ 1,55 Н.

• Список использованных источников

• 1. Эрдеди А.А. Техническая механика: Теоретическая механика. Сопротивление материалов. М.: 2005.
• 2. Автор и источник заимствования неизвестен.

Конец