10 класс. Презентация.

Урок математики в 10 классе: «Симметрия в пространстве. Элементы симметрии правильных многогранников»

Подготовила Л.И. Гоптарь.

Симметрия в пространстве.

Элементы симметрии

правильных многогранников

«Раз, стоя перед черной доской и рисуя на ней мелом разные фигуры, я вдруг был поражен мыслью: почему симметрия приятна для глаз? Что такое симметрия? Это врожденное чувство, отвечал я сам себе. На чем же оно основано? Разве во всём в жизни есть симметрия?»

Л. Н. Толстой «Отрочество»

Толковый словарь русского языка В.И. Даля:

СИММЕТРИЯ - соразмер, соразмерность, равномерие, равнообразие, соответствие, сходность; одинаковость, либо соразмерное подобие расположения частей целого, двух половин.

Новый словарь русского языка Т.Ф. Ефремовой:

СИММЕТРИЯ - соразмерное, пропорциональное расположение частей чего-либо по отношению к центру, середине.

Толковый словарь русского языка Д.Н.Ушакова:

СИММЕТРИЯ - пропорциональность, соразмерность в расположении частей целого в пространстве, полное соответствие (по расположению, величине) одной половины целого другой половине.

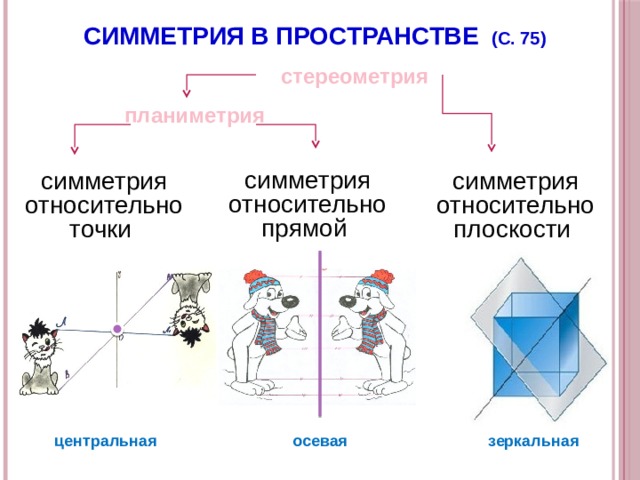
СИММЕТРИЯ В ПРОСТРАНСТВЕ (С. 75)

стереометрия

планиметрия

симметрия относительно прямой

симметрия относительно точки

симметрия относительно плоскости

центральная

осевая

зеркальная

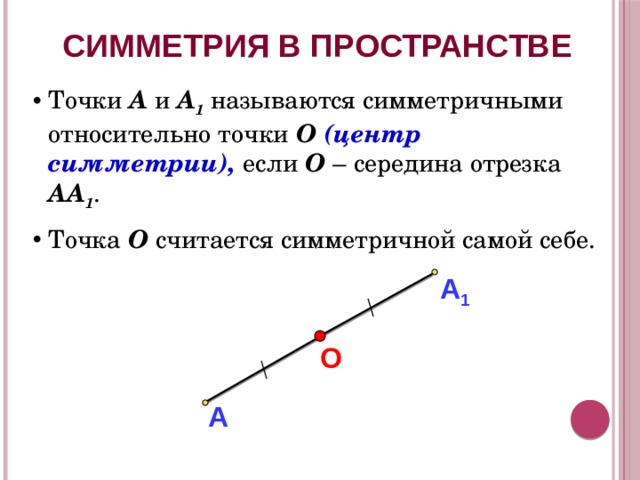
СИММЕТРИЯ В ПРОСТРАНСТВЕ

• Точки А и А 1 называются симметричными относительно точки О (центр симметрии), если О – середина отрезка АА 1 .
• Точка О считается симметричной самой себе.

А 1

О

А

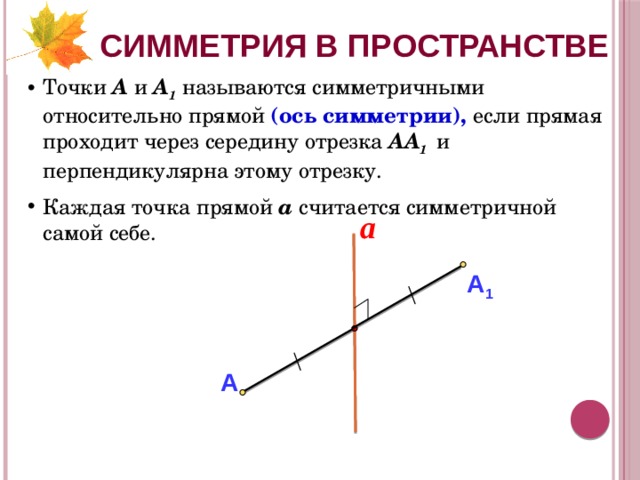
СИММЕТРИЯ В ПРОСТРАНСТВЕ

• Точки А и А 1 называются симметричными относительно прямой (ось симметрии), если прямая проходит через середину отрезка АА 1 и перпендикулярна этому отрезку.
• Каждая точка прямой а считается симметричной самой себе.

a

А 1

А

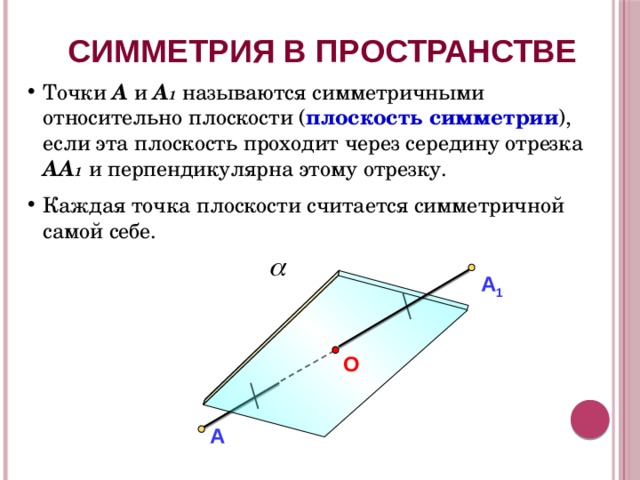
СИММЕТРИЯ В ПРОСТРАНСТВЕ

• Точки А и А 1 называются симметричными относительно плоскости ( плоскость симметрии ), если эта плоскость проходит через середину отрезка АА 1 и перпендикулярна этому отрезку.
• Каждая точка плоскости считается симметричной самой себе.

А 1

О

А

СИММЕТРИЯ В ПРОСТРАНСТВЕ

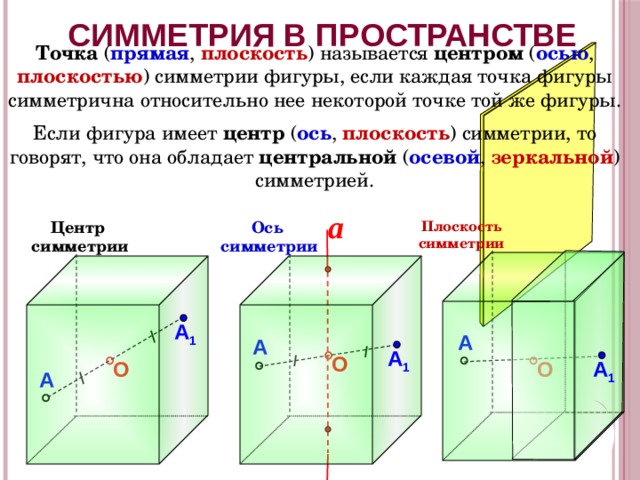
Точка ( прямая , плоскость ) называется центром ( осью , плоскостью ) симметрии фигуры, если каждая точка фигуры симметрична относительно нее некоторой точке той же фигуры.

Если фигура имеет центр ( ось , плоскость ) симметрии, то говорят, что она обладает центральной ( осевой , зеркальной ) симметрией.

a

Ось

Центр

Плоскость симметрии

симметрии

симметрии

«Геометрия 10-11» Л.С. Атанасян и др.

А 1

А

А

А 1

О

А 1

О

О

А

8

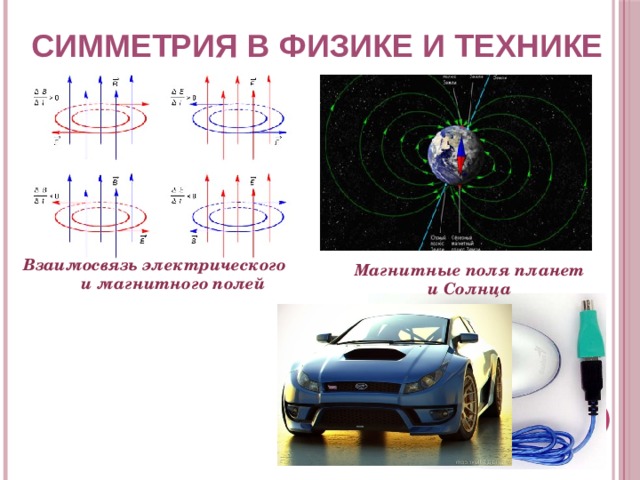
СИММЕТРИЯ В ФИЗИКЕ И ТЕХНИКЕ

Взаимосвязь электрического и магнитного полей

Магнитные поля планет и Солнца

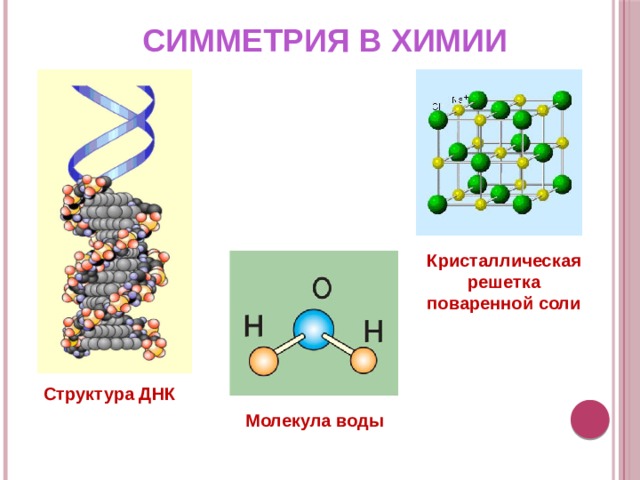
СИММЕТРИЯ В ХИМИИ

Кристаллическая решетка поваренной соли

Структура ДНК

Молекула воды

СИММЕТРИЯ В БИОЛОГИИ (биосимметрика)

СИММЕТРИЯ В АРХИТЕКТУРЕ

Здание МГУ в Москве

Большой дворец в Стрельне

Константиновский дворец

Церковь Покрова Богородицы

СИММЕТРИЯ В АРХИТЕКТУРЕ

«Геометрия 10-11» Л.С. Атанасян и др.

8

СИММЕТРИЯ В ИСКУССТВЕ

Сальвадор Дали «Тайная вечеря»

Микеланджело

Гробница Джулиано Медичи

Обладает ли симметрией лицо человека?

Многогранник – поверхность, составленная из многоугольников и ограничивающая некоторое геометрическое тело.

Правильный многогранник

Выпуклый многогранник называется правильным, если все его грани – равные правильные многоугольники и в каждой его вершине сходится равное число ребер .

«Геометрия 10-11» Л.С. Атанасян и др.

8

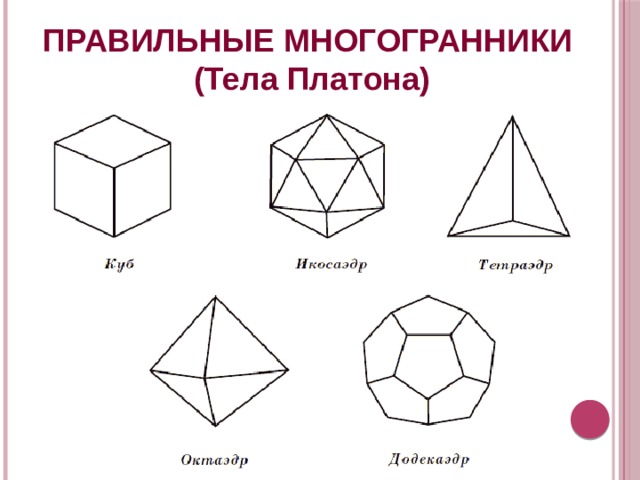
ПРАВИЛЬНЫЕ МНОГОГРАННИКИ

(Тела Платона)

Куб (гексаэдр) – составлен из шести квадратов.

Каждая вершина куба является вершиной трех квадратов.

Состав:

6 граней, 8 вершин и 12 ребер

«Геометрия 10-11» Л.С. Атанасян и др.

Элементы симметрии куба:

• один центр симметрии – точку пересечения его диагоналей;
• осей симметрии – 9.

8

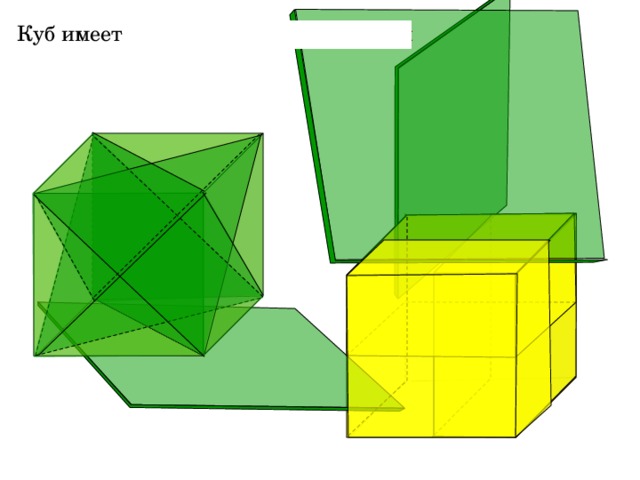
Куб имеет 9 плоскостей симметрии

«Геометрия 10-11» Л.С. Атанасян и др.

8

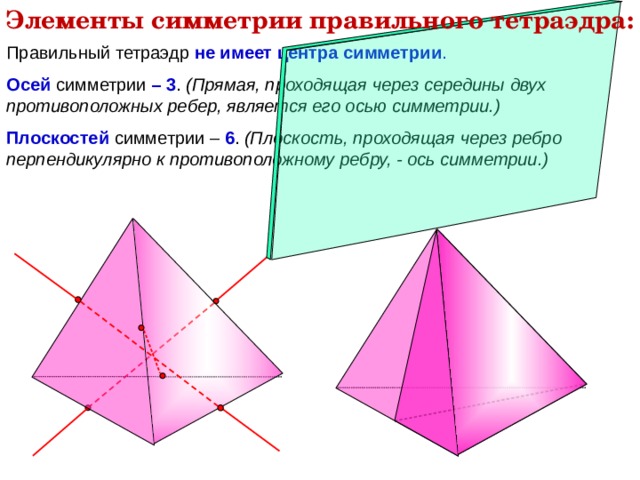
Элементы симметрии правильного тетраэдра:

Правильный тетраэдр не имеет центра симметрии .

Осей симметрии – 3 . (Прямая, проходящая через середины двух противоположных ребер, является его осью симметрии.)

Плоскостей симметрии – 6 . (Плоскость, проходящая через ребро перпендикулярно к противоположному ребру, - ось симметрии.)

«Геометрия 10-11» Л.С. Атанасян и др.

8

ЗАДАНИЕ: Какой из представленных физических приборов обладает осевой симметрией?

1

2

4

3

ЗАДАНИЕ: Определите количество осей симметрии изображения.

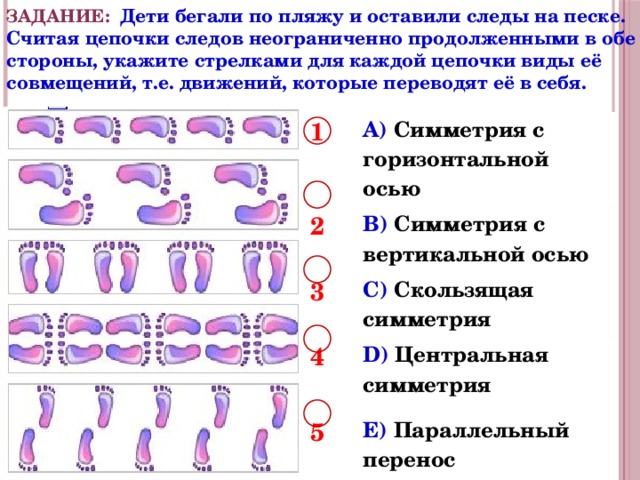
ЗАДАНИЕ: Дети бегали по пляжу и оставили следы на песке. Считая цепочки следов неограниченно продолженными в обе стороны, укажите стрелками для каждой цепочки виды её совмещений, т.е. движений, которые переводят её в себя.

1

2

A) Симметрия с горизонтальной осью

3

B) Симметрия с вертикальной осью

4

5

C) Скользящая симметрия

D) Центральная симметрия

E) Параллельный перенос

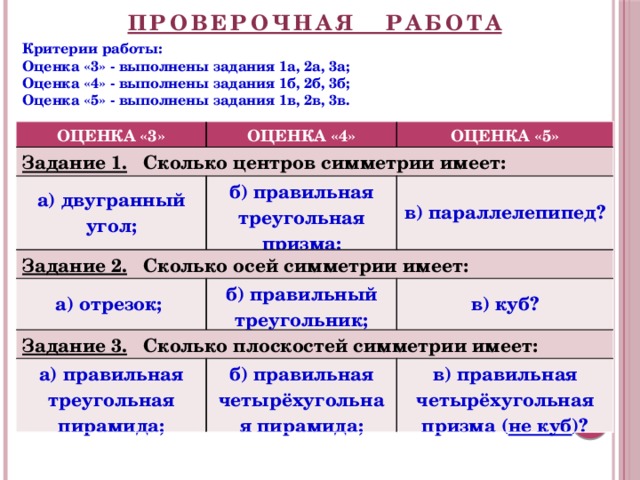
ПРОВЕРОЧНАЯ РАБОТА

Критерии работы:

Оценка «3» - выполнены задания 1а, 2а, 3а;

Оценка «4» - выполнены задания 1б, 2б, 3б;

Оценка «5» - выполнены задания 1в, 2в, 3в.

ОЦЕНКА «3»

ОЦЕНКА «4»

Задание 1. Сколько центров симметрии имеет:

ОЦЕНКА «5»

а) двугранный угол;

б) правильная треугольная призма;

Задание 2. Сколько осей симметрии имеет:

в) параллелепипед?

а) отрезок;

б) правильный треугольник;

Задание 3. Сколько плоскостей симметрии имеет:

в) куб?

а) правильная треугольная пирамида;

б) правильная четырёхугольная пирамида;

в) правильная четырёхугольная призма ( не куб )?

ОТВЕТЫ:

ОЦЕНКА «3»

ОЦЕНКА «4»

Задание 1. Сколько центров симметрии имеет:

ОЦЕНКА «5»

а) не имеет;

Задание 2. Сколько осей симметрии имеет:

б) не имеет;

в) один;

а) бесконечно много;

б) три;

Задание 3. Сколько плоскостей симметрии имеет:

в) девять;

а) три

(или шесть );

б) четыре;

в) пять.

РЕФЛЕКСИЯ:

На уроке мне ОЧЕНЬ понравилось…

На уроке мне НЕ понравилось, ЧТО…

……………

Хотел бы еще УЗНАТЬ о…

……………

……………

СПАСИБО ЗА УРОК!

Список литературы и сайтов:

• Атанасян Л.С., Бутузов В.Ф и др. Геометрия 10-11: базовый и профильный уровни – М.: Просвещение, 2010
• Смирнова И.М. В мире многогранников. М., 1990.
• Шафрановский И.И. Симметрия в природе. Л., 1988.
• http://eor.edu.ru/ - Федерального портала ФЦИОР
• http://school-collection.edu.ru/ - Единая коллекция цифровых образовательных ресурсов (ЦОР)
• http :// nips . riss - telecom . ru / poli /