10 класс. Решение задач.

КОУ ВО « ЛПДО»

Разработка уроков-консультаций

по математике в 10 классе

по теме

РЕШЕНИЕ ЗАДАЧ

НА ПОСТРОЕНИЕ СЕЧЕНИЙ.

Подготовила

Гоптарь Л.И.

-ВОРОНЕЖ-

2020 г.

Базовый учебник: Л.С. Атанасян «Геометрия. Базовый и профильный уровень. 10-11 классы».

Цель урока:

учить решать задачи на построение сечений тетраэдра и параллелепипеда.

Планируемые результаты:

Личностные УУД

- аргументировано оценивать свои и чужие поступки;

- ответственное отношение к учению на основе мотивации к учению и познанию

Предметные УУД

- знать понятия секущей плоскости, сечения тетраэдра и параллелепипеда;

- строить сечения тетраэдра и параллелепипеда.

Метапредметные УУД познавательные

- анализировать и обобщать;

- классифицировать;

- устанавливать аналогии (создавать модели объектов).

регулятивные

- выполнять учебное действие в соответствии с планом;

-оценивать степень и способы достижения цели.

коммуникативные

- различать в речи другого мнения, доказательства, факты;

- корректировать своё мнение;

- организовывать работу в паре;

- использовать ИКТ.

Формы работы обучающихся: фронтальная, парная.

Необходимое техническое оборудование: раздаточный материал, учебник.

ХОД УРОКА.

1. Организационный этап.

Готовность к уроку.

2. Постановка цели и задач. Мотивация учебной деятельности.

- Здравствуйте, дети. Какие фигуры мы рассматривали на прошлом уроке?

О: На прошлом уроке мы рассматривали тетраэдр и параллелепипед. Учились изображать эти многогранники на плоскости.

- Сегодня мы будем учиться решать задачи на построение сечений тетраэдра и параллелепипеда. Для этого сначала узнаем, что такое сечение, как строить сечения и параллельно проведём небольшую классификацию возможных сечений тетраэдра и параллелепипеда.

2. Актуализация знаний.

Рассматривая чертёж ответьте на вопросы:

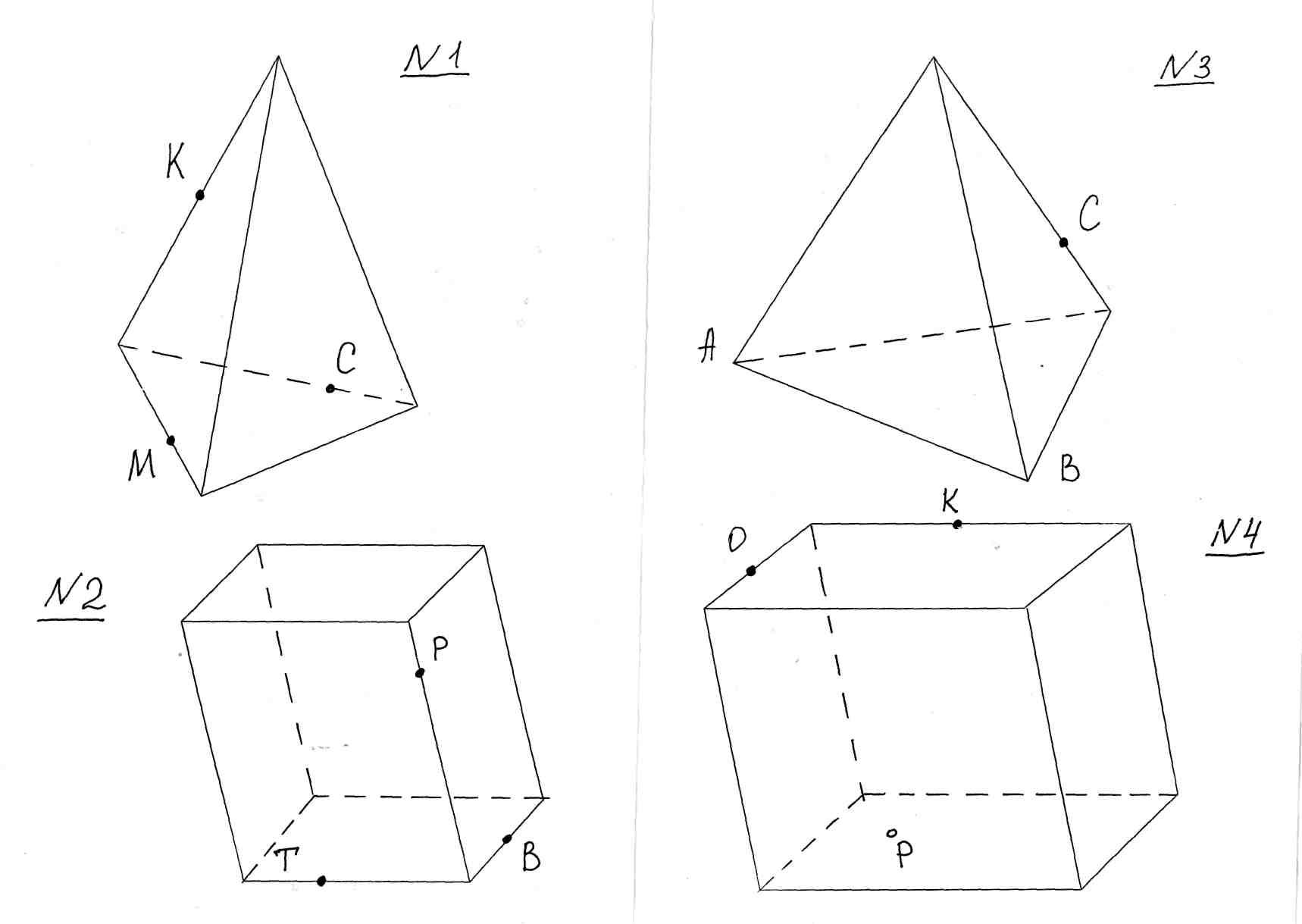
1. (тетраэдр) Назовите прямую, по которой пересекаются плоскости

АВС и АDС; АВК и СDB.

2. Точки пересечения DК и АВС; КSи АВС.

3. Каким граням принадлежит точка К.

4. (Параллелепипед) Пересечение плоскостей АА₁В₁ и АСD; РВС и А₁D₁С₁

5. Точки пересечения РМ и АВС; СМ и А₁D₁С_1.

6. Каким граням принадлежит точка М.

3. Первичное усвоение новых знаний.

- Что же такое сечение? Проведём секущую плоскость, т.е. плоскость, по обе стороны от которой есть точки многогранника.

- Эта секущая плоскость пересекает грани тетраэдра по каким фигурам?

О: секущая плоскость пересекает грани по отрезкам.

- Многоугольник, сторонами которого являются эти отрезки, называется сечением тетраэдра (параллелепипеда).

Многоугольник. А у нас на модели четырёхугольник. Что это значит? – значит в зависимости от того, сколько граней многогранника пересечёт секущая плоскость, столько сторон будет у многоугольника в сечении.

У тетраэдра сколько граней? Значит, в сечении могут получиться только треугольник и четырёхугольник.

У параллелепипеда шесть граней значит, в сечении может получиться только треугольник, четырёхугольник, пятиугольник и шестиугольник.

Давайте рассмотрим все возможные случаи построения. Перейдём к изображениям.

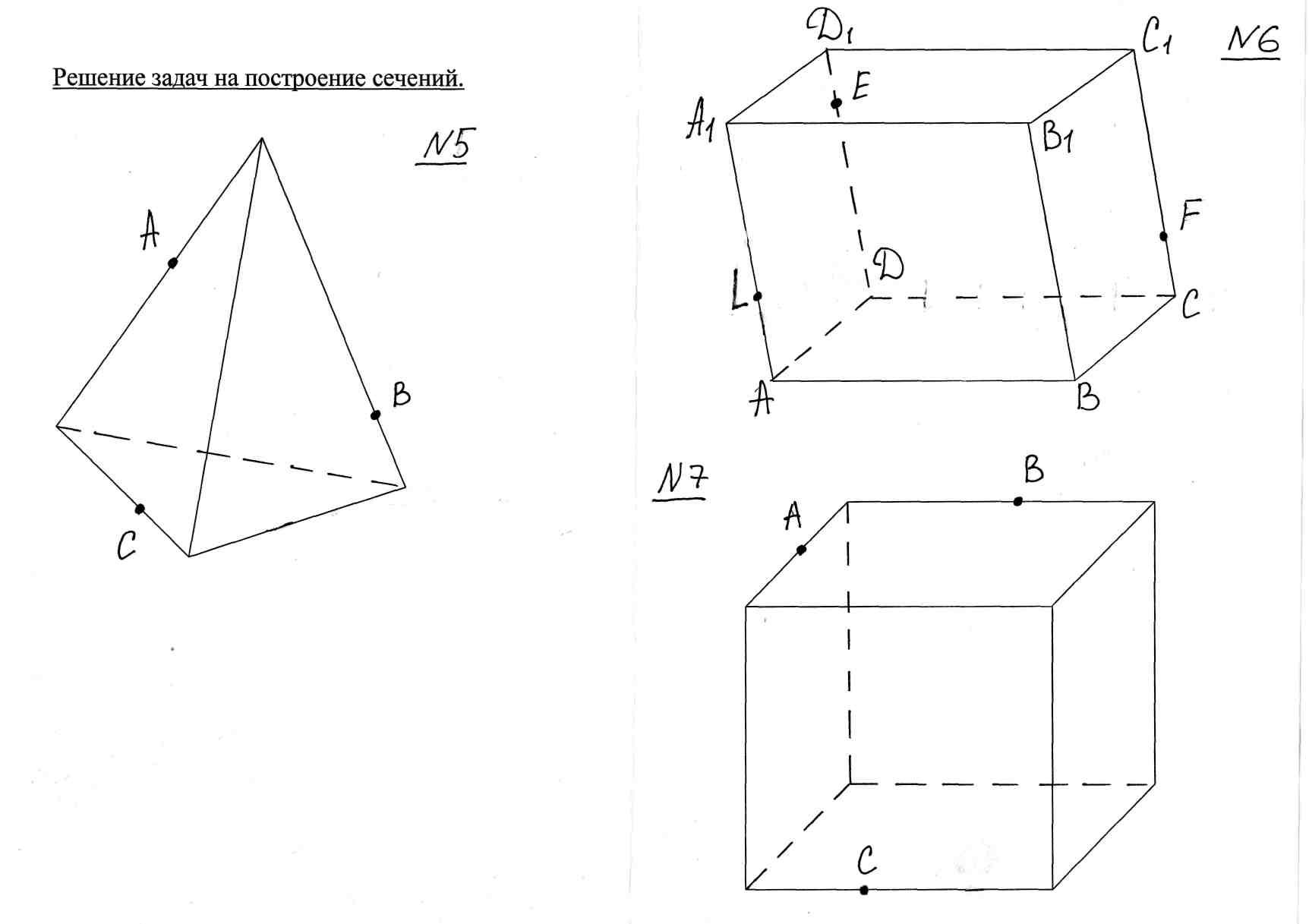
Ф1. Даны три точки. Построить сечение тетраэдра плоскостью.

- Достаточно ли данных для построения?

О: Да, через три точки, не лежащие на одной прямой …

Знаем, что секущая плоскость пересечёт эту грань по отрезку. Две точки этого отрезка известны. Как построить линию пересечения?

О: соединить точки.

NB: две точки сечения лежат в одной грани, значит соединяем их отрезком.

Наш треугольник изображён некорректно.

Как изображаются отрезки, лежащие на невидимых гранях?

О: Они изображаются пунктирными линиями.

Ф2. Параллелепипед. Даны три точки. (Рассматриваем рисунки. Проводим аналогичные рассуждения).

Ф4. Провести сечение через три точки. Точка Р лежит в нижней невидимой грани параллелепипеда.

Точка Р и отрезок ОК лежат в параллельных плоскостях. Т.е. секущая плоскость пересекает две параллельные плоскости. Что произойдёт?

О: Секущая плоскость пересечёт параллельные плоскости по параллельным отрезкам. Получили по две точки в каждой грани. Их можно соединить.

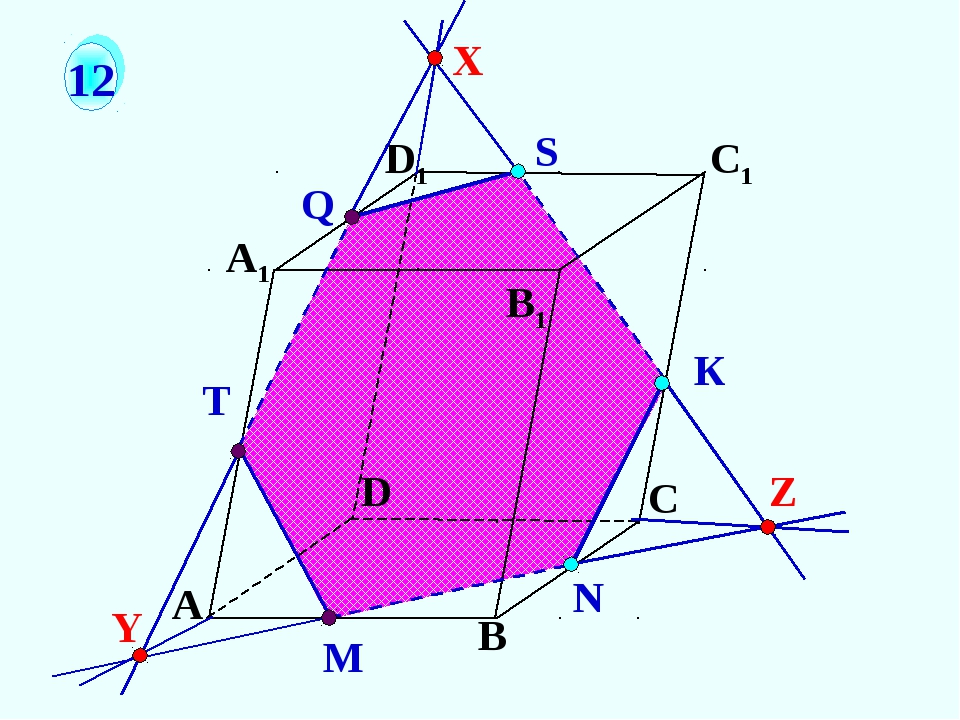
Ф5. Соединяем точки А и С, А и В. Надо построить ещё одну точку, принадлежащую двум граням, содержащим точки и плоскости сечения. Эта точка лежит на линии пересечения граней. Продолжаем…

Ф6. При построении сечений параллелепипеда помним всегда свойство линий пересечения параллельных плоскостей с секущей плоскостью. В нашем случае это секущая плоскость. Найдём ещё одну точку пересечения секущей

плоскости и нижней грани. Эти точки лежат в одной плоскости. Соединяем

их…

Физминутка.

Поухаживаем за своим зрением.

Посмотреть на переносицу и задержать взор на счёт 1-4. До усталости глаза не доводить. Затем открыть глаза, посмотреть вдаль на счёт 1-6. Повторить ещё раз.

Ф7. Аналогичные рассуждения.

5. Первичная проверка понимания и закрепление.

Ф3. Провести сечение через ребро АВ и точку С. Достаточно ли данных для построения? Выполняют самостоятельно.

- Какой теоретический материал поможет строить сечения тетраэдра и параллелепипеда?

О: аксиома стереометрии об общей точке двух плоскостей;

свойстве линий пересечения параллельных плоскостей с секущей плоскостью.

- какие многоугольники могут получиться в сечении тетраэдра и параллелепипеда?

О: треугольники, четырёхугольники. А у параллелепипеда ещё пятиугольник и шестиугольник.

6. Информация о дополнительном задании, инструктаж.

- На следующем уроке продолжим работать над этой темой.

- Д.З. п.14, № 69, 82 (1)

7. Рефлексия. Оценки.

Анализ анкеты карты рефлексии. Подведение итогов урока.

РАЗДАТОЧНЫЙ МАТЕРИАЛ