КОУ ВО «ЦЛПДО»
Разработка урока-консультации в 10 классе.
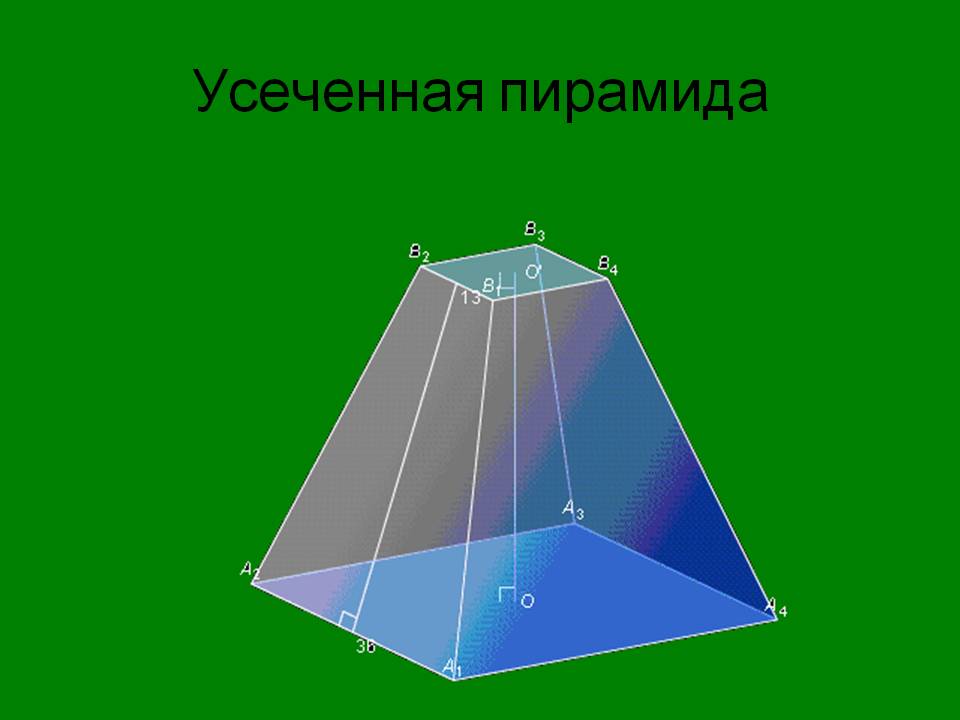
«Усечённая пирамида».
Подготовила
Л.И. Гоптарь.
-Воронеж-
2020г.
Цель:
обеспечить прочное и сознательное овладение учащимися знаниями по данной теме «Усечённая пирамида» и сформировать навыки по их применению для решения задач.
Задачи урока:
Образовательные:
-
учащиеся знакомятся с усеченной пирамидой, знакомятся с её элементами, выводят формулу боковой поверхности усеченной пирамиды;
-
дать понятие усеченной пирамиды и её элементов;
-
рассмотреть различные виды усеченных пирамид;
-
доказать формулу нахождения площади поверхности усеченной пирамиды; научиться применять полученные знания при решении задач.
Развивающие:
-
развивать логическое мышление; пространственное воображение учащихся, умение самостоятельно мыслить, делать выводы, поддержание интереса к математике, развитие познавательного интереса к предмету.
-
развивать у учащихся навыки самостоятельной работы и работы в парах.
Воспитательные:
-
воспитание познавательной активности, культуры общения, ответственности, самостоятельное развитие зрительной памяти;
-
воспитывать у учащихся самостоятельность, любознательность, сознательное отношение к изучению математики;
-
обоснование выбора методов, средств и форм обучения;
-
оптимизировать обучение путем разумного сочетания и соотношения методов, средств и форм, направленных на получение высокого результата за время урока.
Тип урока: урок изучения нового материала и решение задач.
Ход урока.
II. Актуализация знаний (слайды 2 - 3).
1) Теоретический опрос.
-
Какая пирамида называется правильной?
-
Как находится площадь боковой поверхности правильной пирамиды?
-
Чему равна площадь полной поверхности пирамиды?
-
Вспомним определение трапеции
-
Какие виды трапеций вам известны?
-
Как найти площадь трапеции?
2) Устное решение задач (слайды 4 - 5).
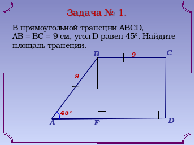
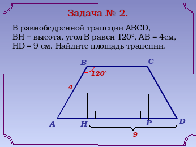
III. Объяснение нового материала.
1) Учитель показывает слайды 6 - 11 с изображением архитектурных сооружений в виде усечённой пирамиды.
Учащимся сообщается тема урока и цели, подчеркивается актуальность данной темы.
2) Объяснение материала проходит в форме беседы, учащиеся в тетрадях делают соответствующие записи.
Изобразите произвольную пирамиду РА1А2…Аn. Проведем секущую плоскость α, параллельную плоскости β основания пирамиды и пересекающую боковые ребра в точках В1, В2,…,Вn (слайд 12).
Плоскость параллельная основанию пирамиды, разбивает её на два многогранника. Один из них является пирамидой, а другой называется усечённой пирамидой.
Усеченная пирамида – это часть полной пирамиды, заключенная между её основанием и секущей плоскостью, параллельной основанию данной пирамиды (слайд 13).
Определение. Усечённая пирамида – многогранник, гранями которого являются два n – угольника А1А2 … Аn и В1В2 … Вn , расположенные в параллельных плоскостях, и n – четырёхугольников А1В1В2А2, А2В2В3А3, … ,Аn Вn В1А1.
Многоугольники А1А2А3 … Аn и В1В2В3 … Вn - нижнее и верхнее основания усечённой пирамиды (слайд 14).
Отрезки А1В1, А2В2, А3В3… - боковые ребра усечённой пирамиды
Четырёхугольники А1В1В2А2, А2В2В3А3 … - боковые грани усечённой пирамиды.
Отрезок РН – перпендикуляр, проведённый из какой-нибудь точки верхнего основания к нижнему основанию – называется высотой усечённой пирамиды (слайд 15).
Рассмотрим виды усечённых пирамид (слайд 16).
3) Работа в парах.
Докажите, что боковые грани усечённой пирамиды являются трапециями.
Доказательство (слайд 17).
Рассмотрим четырехугольник А1В1В2А2.
1. α ║ β
(SА2А3) ∩ α = А2А3
(SА2А3) ∩ β = В2В3
Значит, А2А3 ║ В2В3
Т.о. А1В1В2А2 – трапеция по определению.
Аналогично доказывается и про остальные боковые грани.
4) Правильная усечённая пирамида.
Учитель показывает натуральные модели правильных пирамид и правильных усечённых пирамид. Как вы думаете, какая усечённая пирамида будет правильной? Что лежит в её основаниях?
Определение. Усеченная пирамида называется правильной, если она получена сечением правильной пирамиды плоскостью, параллельной основанию.
Высота боковой грани называется апофемой (слайд 18).
Давайте посмотрим на модели правильных усечённых пирамид, что вы можете сказать об их основаниях? А о боковых гранях? Сравните их.
Таким образом, правильная призма обладает следующими свойствами. Основания - правильные многоугольники.
Боковые грани – равные равнобедренные трапеции (слайд 19).
Как вы думаете, что называют площадью полной поверхности усечённой пирамиды?
Площадью полной поверхности усечённой пирамиды называется сумма площадей всех её граней: оснований и всех боковых граней.
Sполн. = Sбок + S верхн. осн. + Sнижн. осн
А что такое площадь боковой поверхности усечённой пирамиды?
Площадью боковой поверхности усечённой пирамиды называется сумма площадей её боковых граней.
Вспомним, как найти площадь боковой поверхности правильной пирамиды?
Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
А как найти площадь боковой поверхности правильной усечённой пирамиды? (слайд 19).
Посмотрим на правильную усечённую пирамиду, изображённую на слайде 21.
И поставим перед собой задачу: найти площадь её боковой поверхности.
Один ученик работает на доске.
Какими фигурами являются боковые грани правильной n-угольной усечённой пирамиды? (Равнобедренными трапециями)
Н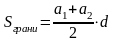 айдем площадь одной из граней правильной n-угольной усечённой пирамиды.
айдем площадь одной из граней правильной n-угольной усечённой пирамиды.
Сколько таких граней? (n)
Т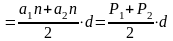
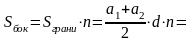 .к. эта усечённая пирамида правильная, то
.к. эта усечённая пирамида правильная, то
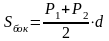
Итак, мы доказали, что
Теорема.
Площадь боковой поверхности правильной усеченной пирамиды равна произведению полусуммы периметров оснований на апофему.
IV. Физкультминутка.
Учитель предлагает простые упражнения для шеи, рук и спины.
V. Закрепление изученного материала.
1) Первичное закрепление.
1 уч-ся с комментированием решает № 268 в тетрадях.
Дано: MABCD - правильная пирамида, А1В1С1|| АВС, МО1: O1O =1: 3, NK - апофема, NK = 4 дм, Syc.пиp. = 186 дм2
Найти: ОО1 - ?
Решение.
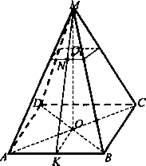
Рассмотрим ΔМКО. Так как NO1 || KO, то МО1 : МО = O1N : OK, значит, стороны В1С1 : ВС = МО1 : МО. В1С1 = 1 : 3.
Пусть В1С1 = х, ВС = 3х. Имеем
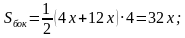
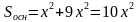
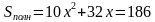
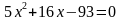
 (не удовлетворяет условию задачи);
(не удовлетворяет условию задачи);
В1С1 = 3 (см), NО = 1,5 (см); ВС = 9 (см), ОК = 4,5 (см); KF = OK – NO1 = 3. Из ΔKNF по теореме Пифагора 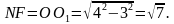
Ответ: 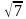 дм.
дм.
2) Самостоятельное решение задач (дифференцированный подход).
Учащимся предлагаются на выбор разноуровневые задания.
1 уровень. Выполняют самостоятельную работу по вариантам. Учитель при необходимости консультирует учащихся, анализирует результаты выполнения учащимися заданий.
Вариант 1
В правильной четырехугольной усеченной пирамиде стороны оснований равны 22см и 6см, а высота-13см. Вычислите площадь полной поверхности пирамиды.
Вариант 2
В правильной четырехугольной усеченной пирамиде стороны оснований равны 24см и 8см, а высота-15см. Вычислите площадь полной поверхности пирамиды.
2 уровень. Работают самостоятельно в микрогруппах (по необходимости пользуются помощью учителя).
Задача.
В пирамиде сечение, параллельное основанию, делит высоту в отношении 3 : 4 (от вершины к основанию), а площадь сечения меньше площади основания на 200 см2. Найдите площадь основания.
VI. Подведение итогов урока, рефлексия деятельности.
Давайте подведем итог.
- Итак, что вы узнали сегодня на уроке?
- Чему научились сегодня на уроке?
- Что такое усеченная пирамида?
- Какая усеченная пирамида называется правильной?
Учитель оценивает учащихся, задает дополнительное задание:
1) п. 30, № 269, 270;
2) дополнительная задача (слайд 19).









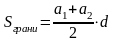 айдем площадь одной из граней правильной n-угольной усечённой пирамиды.
айдем площадь одной из граней правильной n-угольной усечённой пирамиды.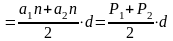
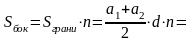 .к. эта усечённая пирамида правильная, то
.к. эта усечённая пирамида правильная, то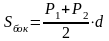

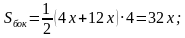
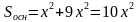
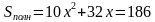
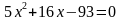
 (не удовлетворяет условию задачи);
(не удовлетворяет условию задачи);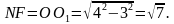
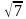 дм.
дм.




















