Муниципальное казённое общеобразовательное учреждение
«Ребрихинская средняя общеобразовательная школа»
Ребрихинского района Алтайского края
Математический тренажёр для подготовки к ОГЭ
тема: Линейная функция. Квадратичная функция. Основные свойства. Распознавание функций,
в том числе: у=к/х, у=√ х
Составитель: Сафенрайтер М.В.
учитель математики
с. Ребриха
Линейная функция и ее график
В этой статье мы рассмотрим линейную функцию, график линейной функции и его свойства. И, как обычно, решим несколько задач на эту тему.
Линейной функцией называется функция вида 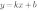
В уравнении функции число 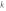 , которое мы умножаем на
, которое мы умножаем на 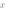 называется коэффициентом наклона.
называется коэффициентом наклона.
Например, в уравнении функции 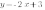
 ;
;
в уравнении функции 
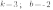 ;
;
в уравнении функции 
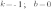 ;
;
в уравнении функции 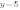
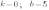 .
.
 Графиком линейной функции является прямая линия.
Графиком линейной функции является прямая линия.
1. Чтобы построить график функции, нам нужны координаты двух точек, принадлежащих графику функции. Чтобы их найти, нужно взять два значения х, подставить их в уравнение функции, и по ним вычислить соответствующие значения y.
Например, чтобы построить график функции 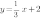 , удобно взять
, удобно взять 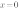 и
и 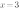 , тогда ординаты эти точек будут равны
, тогда ординаты эти точек будут равны 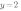 и
и 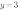 .
.
Получим точки А(0;2) и В(3;3). Соединим их и получим график функции 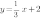 :
:
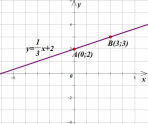
2. В уравнении функции 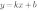 коэффициент
коэффициент 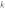 отвечает за наклон графика функции:
отвечает за наклон графика функции:
Коэффициент 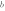 отвечает за сдвиг графика вдоль оси
отвечает за сдвиг графика вдоль оси 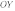 :
:
На рисунке ниже изображены графики функций 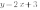 ;
; 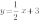 ;
; 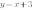

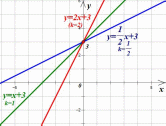
Заметим, что во всех этих функциях коэффициент 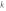 больше нуля, и все графики функций наклонены вправо. Причем, чем больше значение
больше нуля, и все графики функций наклонены вправо. Причем, чем больше значение 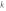 , тем круче идет прямая.
, тем круче идет прямая.
Во всех функциях  - и мы видим, что все графики пересекают ось OY в точке (0;3)
- и мы видим, что все графики пересекают ось OY в точке (0;3)
Теперь рассмотрим графики функций 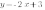 ;
; 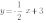 ;
; 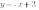

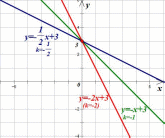
На этот раз во всех функциях коэффициент 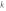 меньше нуля, и все графики функций наклонены влево.
меньше нуля, и все графики функций наклонены влево.
Заметим, что чем больше |k|, тем круче идет прямая. Коэффициент b тот же, b=3, и графики также как в предыдущем случае пересекают ось OY в точке (0;3)
Рассмотрим графики функций 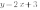 ;
; 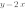 ;
; 
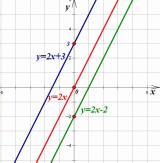
Теперь во всех уравнениях функций коэффициенты 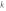 равны. И мы получили три параллельные прямые.
равны. И мы получили три параллельные прямые.
Но коэффициенты b различны, и эти графики пересекают ось OY в различных точках:
График функции 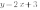 (b=3) пересекает ось OY в точке (0;3)
(b=3) пересекает ось OY в точке (0;3)
График функции 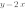 (b=0) пересекает ось OY в точке (0;0) - начале координат.
(b=0) пересекает ось OY в точке (0;0) - начале координат.
График функции  (b=-2) пересекает ось OY в точке (0;-2)
(b=-2) пересекает ось OY в точке (0;-2)
Итак, если мы знаем знаки коэффициентов k и b, то можем сразу представить, как выглядит график функции 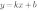 .
.
Если k0, то график функции 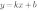 имеет вид:
имеет вид:
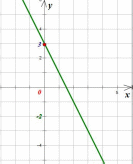
Если k0 и b0, то график функции 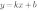 имеет вид:
имеет вид:

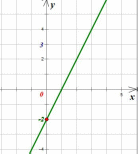
Если k0 и bто график функции 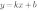 имеет вид:
имеет вид:
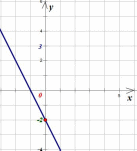
Если kто график функции 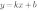 имеет вид:
имеет вид:
Если k=0 , то функция 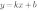 превращается в функцию
превращается в функцию 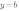 и ее график имеет вид:
и ее график имеет вид:
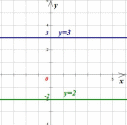
Ординаты всех точек графика функции 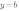 равны
равны 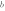
Если b=0, то график функции 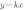 проходит через начало координат:
проходит через начало координат:
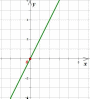
Это график прямой пропорциональности.
3. Отдельно отмечу график уравнения 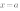 . График этого уравнения представляет собой прямую линию, параллельую оси
. График этого уравнения представляет собой прямую линию, параллельую оси 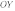 все точки которой имеют абсциссу
все точки которой имеют абсциссу 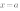 .
.
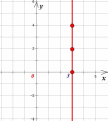
Например, график уравнения 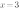 выглядит так:
выглядит так:
Внимание! Уравнение 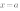 не является функцией, так как различным значениям аргумента соответствует одно и то же значение функции, что не соответствует определению функции.
не является функцией, так как различным значениям аргумента соответствует одно и то же значение функции, что не соответствует определению функции.
4. Условие параллельности двух прямых:
График функции 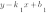 параллелен графику функции
параллелен графику функции  , если
, если 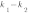
5. Условие перпендикулярности двух прямых:
График функции 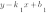 перпендикулярен графику функции
перпендикулярен графику функции  , если
, если 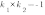 или
или 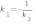
6. Точки пересечения графика функции 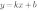 с осями координат.
с осями координат.
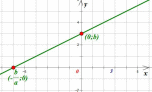
С осью ОY. Абсцисса любой точки, принадлежащей оси ОY равна нулю. Поэтому, чтобы найти точку пересечения с осью ОY нужно в уравнение функции вместо х подставить ноль. Получим y=b. То есть точка пересечения с осью OY имеет координаты (0;b).
С осью ОХ: Ордината любой точки, принадлежащей оси ОХ равна нулю. Поэтому, чтобы найти точку пересечения с осью ОХ нужно в уравнение функции вместо y подставить ноль. Получим 0=kx+b. Отсюда 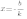 . То есть точка пересечения с осью OX имеет координаты (
. То есть точка пересечения с осью OX имеет координаты (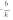 ;0):
;0):
Рассмотрим решение задач.
1. Постройте график функции 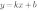 , если известно, что он проходит через точку А(-3;2) и параллелен прямой y=-4x.
, если известно, что он проходит через точку А(-3;2) и параллелен прямой y=-4x.
В уравнении функции 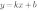 два неизвестных параметра: k и b. Поэтому в тексте задачи должны быть два условия, характеризующих график функции.
два неизвестных параметра: k и b. Поэтому в тексте задачи должны быть два условия, характеризующих график функции.
а) Из того, что график функции 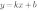 параллелен прямой y=-4x, следует, что k=-4. То есть уравнение функции имеет вид
параллелен прямой y=-4x, следует, что k=-4. То есть уравнение функции имеет вид 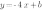
б) Нам осталось найти b. Известно, что график функции 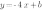 проходит через точку А(-3;2). Если точка принадлежит графику функции, то при подстановке ее координат в уравнение функции, мы получим верное равенство:
проходит через точку А(-3;2). Если точка принадлежит графику функции, то при подстановке ее координат в уравнение функции, мы получим верное равенство:
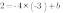 отсюда b=-10
отсюда b=-10
Таким образом, нам надо построить график функции 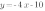
Точка А(-3;2) нам известна, возьмем точку B(0;-10)
Поставим эти точки в координатной плоскости и соединим их прямой:
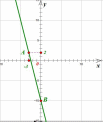
2. Написать уравнение прямой, проходящей через точки A(1;1); B(2;4).
Если прямая проходит через точки с заданными координатами, следовательно, координаты точек удовлетворяют уравнению прямой 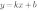 . То есть если мы координаты точек подставим в уравнение прямой, то получим верное равенство.
. То есть если мы координаты точек подставим в уравнение прямой, то получим верное равенство.
Подставим координаты каждой точки в уравнение 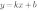 и получим систему линейных уравнений.
и получим систему линейных уравнений.
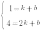
Вычтем из второго уравнения системы первое, и получим 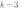 . Подставим значение k в первое уравнение системы, и получим b=-2.
. Подставим значение k в первое уравнение системы, и получим b=-2.
Итак, уравнение прямой 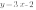 .
.
3. Постройте график уравнения 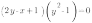
Чтобы найти, при каких значениях неизвестного произведение нескольких множителей равно нулю, нужно каждый множитель приравнять к нулю и учесть ОДЗ каждого множителя.
Это уравнение не имеет ограничений на ОДЗ. Разложим на множители вторую скобку и приравняем каждый множитель к нулю. Получим совокупность уравнений:
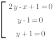

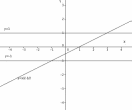
Построим графики всех уравнений совокупности в одной коорднатной плоскости. Это и есть график уравнения 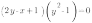 :
:
4. Постройте график функции 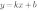 , если он перпендикулярен прямой
, если он перпендикулярен прямой 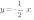 и проходит через точку М(-1;2)
и проходит через точку М(-1;2)
Мы не будем строить график, только найдем уравнение прямой.
а) Так как график функции 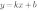 , если он перпендикулярен прямой
, если он перпендикулярен прямой 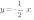 , следовательно
, следовательно 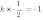 , отсюда
, отсюда 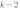 . То есть уравнение функции имеет вид
. То есть уравнение функции имеет вид 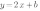
б) Мы знаем, что график функции 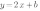 проходит через точку М(-1;2). Подставим ее координаты в уравнение функции. Получим:
проходит через точку М(-1;2). Подставим ее координаты в уравнение функции. Получим:
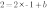 , отсюда
, отсюда  .
.
Следовательно, наша функция имеет вид: 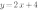 .
.
5. Постройте график функции 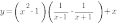
Упростим выражение, стоящее в правой части уравнения функции.
Важно! Прежде чем упрощать выражение, найдем его ОДЗ.
Знаменатель дроби не может быть равен нулю, поэтому 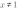
 ,
, 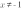
 .
.
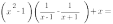
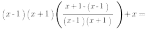
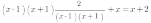
Тогда наша функция принимает вид:
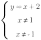

То есть нам надо построить график функции 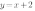 и выколоть на нем две точки: с абсциссами x=1 и x=-1:
и выколоть на нем две точки: с абсциссами x=1 и x=-1:
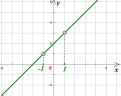
Квадратичная функция и ее график В этой статье мы поговорим о том, что такое квадратичная функция, научимся строить ее график и определять вид графика в зависимости от знака дискриминанта и знака старшего коэффициента.
Итак.
Функция вида 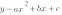 , где
, где 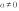
 называется квадратичной функцией.
называется квадратичной функцией.
В уравнении квадратичной функции:
a - старший коэффициент
b - второй коэффициент
с - свободный член.
Графиком квадратичной функции является квадратичная парабола, которая для функции 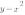 имеет вид:
имеет вид:
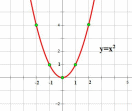
Обратите внимание на точки, обозначенные зелеными кружками - это, так называемые "базовые точки". Чтобы найти координаты этих точек для функции 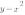 , составим таблицу:
, составим таблицу:
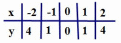
Внимание! Если в уравнении квадратичной функции старший коэффициент 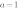 , то график квадратичной функции имеет ровно такую же форму, как график функции
, то график квадратичной функции имеет ровно такую же форму, как график функции 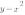 при любых значениях остальных коэффициентов.
при любых значениях остальных коэффициентов.
График функции 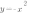 имеет вид:
имеет вид:
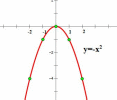
Для нахождения координат базовых точек составим таблицу:
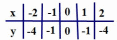
Обратите внимание, что график функции 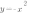 симметричен графику функции
симметричен графику функции 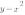 относительно оси ОХ.
относительно оси ОХ.
Итак, мы заметили:
Если старший коэффициент a0, то ветви параболы напрaвлены вверх.
Если старший коэффициент a
Второй параметр для построения графика функции - значения х, в которых функция равна нулю, или нули функции. На графике нули функции 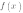 - это точки пересечения графика функции
- это точки пересечения графика функции 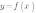 с осью ОХ.
с осью ОХ.
Поскольку ордината (у) любой точки, лежащей на оси ОХ равна нулю, чтобы найти координаты точек пересечения графика функции 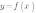 с осью ОХ, нужно решить уравнение
с осью ОХ, нужно решить уравнение 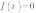 .
.
В случае квадратичной функции 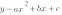 нужно решить квадратное уравнение
нужно решить квадратное уравнение 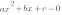 .
.
Теперь внимание!
В процессе решения квадратного уравнения мы находим дискриминант: 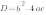 , который определяет число корней квадратного уравнения.
, который определяет число корней квадратного уравнения.
И здесь возможны три случая:
1. Если 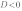
 ,то уравнение
,то уравнение 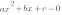 не имеет решений, и, следовательно, квадратичная парабола
не имеет решений, и, следовательно, квадратичная парабола 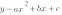 не имеет точек пересечения с осью ОХ. Если
не имеет точек пересечения с осью ОХ. Если 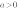
 ,то график функции выглядит как-то так:
,то график функции выглядит как-то так:
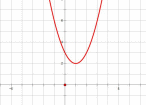
2. Если 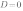
 ,то уравнение
,то уравнение 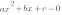 имеет одно решение, и, следовательно, квадратичная парабола
имеет одно решение, и, следовательно, квадратичная парабола 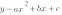 имеет одну точку пересечения с осью ОХ. Если
имеет одну точку пересечения с осью ОХ. Если 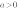
 ,то график функции выглядит примерно так:
,то график функции выглядит примерно так:
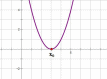
3. Если 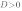
 ,то уравнение
,то уравнение 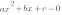 имеет два решения, и, следовательно, квадратичная парабола
имеет два решения, и, следовательно, квадратичная парабола 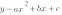 имеет две точки пересечения с осью ОХ:
имеет две точки пересечения с осью ОХ:
 ,
, 
Если 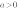
 ,то график функции выглядит примерно так:
,то график функции выглядит примерно так:
Следовательно, зная направление ветвей параболы и знак дискриминанта, мы уже можем в общих чертах определить, как выглядит график нашей функции.
Следующий важный параметр графика квадратичной функции - координаты вершины параболы:
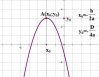

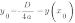
Прямая, проходящая через вершину параболы параллельно оси OY является осью симметрии параболы.
И еще один параметр, полезный при построении графика функции - точка пересечения параболы 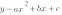 с осью OY.
с осью OY.
Поскольку абсцисса любой точки, лежащей на оси OY равна нулю, чтобы найти точку пересечения параболы 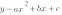 с осью OY, нужно в уравнение параболы вместо х подставить ноль:
с осью OY, нужно в уравнение параболы вместо х подставить ноль: 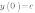 .
.
То есть точка пересечения параболы с осью OY имеет координаты (0;c).
Итак, основные параметры графика квадратичной функции показаны на рисунке:
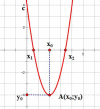
Р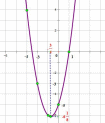 ассмотрим несколько способов построения квадратичной параболы. В зависимости от того, каким образом задана квадратичная функция, можно выбрать наиболее удобный.
ассмотрим несколько способов построения квадратичной параболы. В зависимости от того, каким образом задана квадратичная функция, можно выбрать наиболее удобный.
1. Функция задана формулой 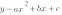 .
.
Рассмотрим общий алгоритм построения графика квадратичной параболы на примере построения графика функции 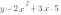
1. Направление ветвей параболы.
Так как 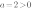
 ,ветви параболы направлены вверх.
,ветви параболы направлены вверх.
2. Найдем дискриминант квадратного трехчлена 
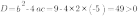

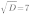
Дискриминант квадратного трехчлена больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ.
Для того, чтобы найти их координаты, решим уравнение: 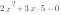
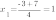 ,
, 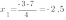
3. Координаты вершины параболы:
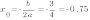
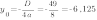
4. Точка пересечения параболы с осью OY: (0;-5),и ей симметричная относительно оси симметрии параболы.
Нанесем эти точки на координатную плоскость, и соединим их плавной кривой:
Этот способ можно несколько упростить.
1. Найдем координаты вершины параболы.
2. Найдем координаты точек, стоящих справа и слева от вершины.
Воспользуемся результатами построения графика функции
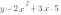
Координаты вершины параболы
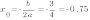
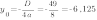
Ближайшие к вершине точки, расположенные слева от вершины имеют абсциссы соответственно -1;-2;-3
Ближайшие к вершине точки, расположенные справа имеют абсциссы соответственно 0;1;2
Подставим значения х в уравнение функции, найдем ординаты этих точек и занесем их в таблицу:

Нанесем эти точки на координатную плоскость и соединим плавной линией: 
2. Уравнение квадратичной функции имеет вид 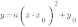 - в этом уравнении
- в этом уравнении 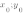 - координаты вершины параболы
- координаты вершины параболы
или в уравнении квадратичной функции 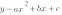
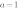 , и второй коэффициент - четное число.
, и второй коэффициент - четное число.
Построим для примера график функции 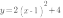 .
.
Вспомним линейные преобразования графиков функций. Чтобы построить график функции 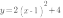 , нужно
, нужно
-
сначала построить график функции 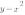 ,
,
-
затем одинаты всех точек графика умножить на 2,
-
затем сдвинуть его вдоль оси ОХ на 1 единицу вправо,
-
а затем вдоль оси OY на 4 единицы вверх:
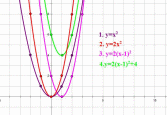
Теперь рассмотрим построение графика функции 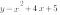 . В уравнении этой функции
. В уравнении этой функции 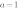 , и второй коэффициент - четное число.
, и второй коэффициент - четное число.
Выделим в уравнении функции полный квадрат: 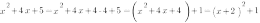
Следовательно, координаты вершины параболы: 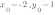 . Старший коэффициент равен 1, поэтому построим по шаблону параболу с вершиной в точке (-2;1):
. Старший коэффициент равен 1, поэтому построим по шаблону параболу с вершиной в точке (-2;1):
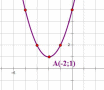
3. Уравнение квадратичной функции имеет вид y=(x+a)(x+b)
Построим для примера график функции y=(x-2)(x+1)
1. Вид уравнения функции позволяет легко найти нули функции - точки пересечения графика функции с осью ОХ:
(х-2)(х+1)=0, отсюда 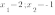
2. Координаты вершины параболы: 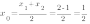
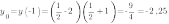
3. Точка пересечения с осью OY: с=ab=(-2)(1)=-2 и ей симметричная.
Нанесем эти точки на координатную плоскость и построим график:
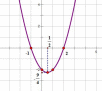
Функция y=k/x
Коэффициент k может принимать любые значения, кроме k=0. Рассмотрим сначала случай, когда k=1; таким образом, сначала речь пойдёт о функции y=1/x.
Чтобы построить график функции y=1/x, дадим независимой переменной x несколько конкретных значений и вычислим (по формулe y=1/x) соответствующие значения зависимой переменной y. Правда, на этот раз удобнее проводить вычисления и построения постепенно, сначала придавая аргументу только положительные значения, а затем — только отрицательные.
Первый этап. Если x=1, то y=1 (напомним, что мы пользуемся формулой y=1/x);
если x=2, то y=1/2;
если x=4, то y=1/4;
если x=8, то y=1/8;
если x=1/2, то y=2;
если x=1/4, то y=4;
если x=1/8 , то y=8.
Короче говоря, мы составили следующую таблицу:
| x | 1 | 2 | 4 | 8 | 1/2 | 1/4 | 1/8 |
| y | 1 | 1/2 | 1/4 | 1/8 | 2 | 4 | 8 |
Построим найденные точки на координатной плоскости.

Второй этап.
если x=−1, то y=−1;
если x=−2, то y=−1/2;
если x=−4, то y=−1/4;
если x=−8, то y=−1/8;
если x=−1/2, то y=−2;
если x=−1/4, то y=−4;
еслиx=−1/8, то y=−8.
Составим следующую таблицу:
| x | −1 | −2 | −4 | −8 | −1/2 | −1/4 | −1/8 |
| y | −1 | −1/2 | −1/4 | −1/8 | −2 | −4 | −8 |
Построим найденные точки на координатной плоскости.

А теперь объединим два этапа в один, т. е. из двух рисунков сделаем один.
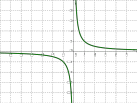
Это и есть график функции y=1/x, его называют гиперболой.
Попробуем по чертежу описать геометрические свойства гиперболы.
Во-первых, замечаем, что эта линия выглядит так же красиво, как парабола, поскольку обладает симметрией. Любая прямая, проходящая через начало координат O и расположенная в первом и третьем координатных углах, пересекает гиперболу в двух точках, которые лежат на этой прямой по разные стороны от точки O, но на равных расстояниях от неё. Это присуще, в частности, точкам (1;1) и (−1;−1), (2;1/2) и (−2;−1/2) и т. д.
Значит, O — центр симметрии гиперболы. Говорят также, что гипербола симметрична относительно начала координат.
Во-вторых, видим, что гипербола состоит из двух симметричных относительно начала координат частей; их обычно называют ветвями гиперболы.
В-третьих, замечаем, что каждая ветвь гиперболы в одном направлении подходит всё ближе и ближе к оси абсцисс, а в другом направлении — к оси ординат. В подобных случаях соответствующие прямые называют асимптотами.
Значит, график функции y=1/x, т.е. гипербола, имеет две асимптоты: ось x и ось y.
Если внимательно проанализировать построенный график, то можно обнаружить ещё одно геометрическое свойство, не такое очевидное, как три предыдущих (математики обычно говорят так: «более тонкое свойство»).
Обрати внимание!
У гиперболы имеется не только центр симметрии, но и оси симметрии.
В самом деле, построим прямую y=x.
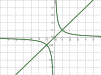
Теперь смотрите: точки (2;1/2) и (1/2;2) расположены по разные стороны от проведённой прямой, но на равных расстояниях от неё. Они симметричны, относительно этой прямой. Тоже можно сказать о точках (4;1/4) и (1/4;4),(8;1/8) и (1/8;8) и т.д. Значит, прямая y=x — ось симметрии гиперболы y=1x ( равно как и y=−x).
Функция у = √х , ее свойства и график
Для построения графика функции 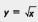 дадим, как обычно, независимой переменной х несколько конкретных значений (неотрицательных, поскольку при х
дадим, как обычно, независимой переменной х несколько конкретных значений (неотрицательных, поскольку при х  не имеет смысла) и вычислим соответствующие значения зависимой переменной у. Разумеется, мы будем давать х такие значения, для которых известно точное значение квадратного корня. Итак:
не имеет смысла) и вычислим соответствующие значения зависимой переменной у. Разумеется, мы будем давать х такие значения, для которых известно точное значение квадратного корня. Итак:

Итак, мы составили таблицу значений функции:
| x | 0 | 1 | 4 | 6,25 | 9 |
| y | 0 | 1 | 2 | 2,5 | 3 |
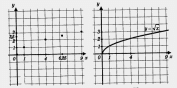
Построим найденные точки (0; 0), (1;1), (4; 2), (6,25; 2,5), (0;3) на координатной плоскости (рис. 78). Они располагаются некоторой линии, начертим ее (рис. 79). Получили график функции 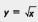 . Обратите внимание: график касается оси у в точке (0; 0). Заметим, что, имея шаблон параболы у = х2, можно без труда с его помощью построить график функции
. Обратите внимание: график касается оси у в точке (0; 0). Заметим, что, имея шаблон параболы у = х2, можно без труда с его помощью построить график функции 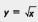 , ведь это — ветвь той же параболы, только ориентированная не вверх, а вправо.
, ведь это — ветвь той же параболы, только ориентированная не вверх, а вправо.
Свойства функции 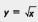
Описывая свойства этой функции, мы, как обычно, будем опираться на ее геометрическую модель — ветвь параболы (рис. 79).
1. Область определения функции — луч [0, +оо).
2. у = 0 при х = 0; у 0 при х 0.
3. Функция возрастает на луче [0, + оо).
4. Функция ограничена снизу, но не ограничена сверху.
5. унаим. = 0 (достигается при х = 0), унаи6 не существует.
6. Функция непрерывна на луче [0, +оо).
Комментариев требует лишь свойство 4. Почему мы считаем, что функция не ограничена сверху? Возьмем, например, число 10. Найдется ли такое значение х, для которого будет выполнено неравенство  10? Конечно, достаточно взять х = 121, ведь
10? Конечно, достаточно взять х = 121, ведь 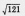 = 11, а 11 10. Возьмем число 40. Найдется ли такое значение х, для которого будет выполняться неравенство
= 11, а 11 10. Возьмем число 40. Найдется ли такое значение х, для которого будет выполняться неравенство  40? Конечно, достаточно взять х = 2500, ведь
40? Конечно, достаточно взять х = 2500, ведь 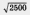 = 50, а 50 40. И вообще, какое бы положительное число т ни взять, всегда найдется такое х, что будет выполняться неравенство
= 50, а 50 40. И вообще, какое бы положительное число т ни взять, всегда найдется такое х, что будет выполняться неравенство  m (достаточно взять х = (m + 1)2; подумайте, почему это так).
m (достаточно взять х = (m + 1)2; подумайте, почему это так).
А теперь обратим внимание на одно любопытное обстоятельство. Рассмотрим две функции: у =  (ее график изображен на рис. 79) и у = х2, где х 0 (ее график изображен на рис. 80). Мы только что перечислили шесть свойств для первой функции, но абсолютно теми же свойствами обладает и вторая функция. Словесные «портреты» двух различных функций одинаковы. Математики не смогли вынести такой несправедливости, когда разные функции, имеющие разные графики, словесно описываются одинаково. Они обнаружили принципиальные различия в характере графиков, заметив, что график функции
(ее график изображен на рис. 79) и у = х2, где х 0 (ее график изображен на рис. 80). Мы только что перечислили шесть свойств для первой функции, но абсолютно теми же свойствами обладает и вторая функция. Словесные «портреты» двух различных функций одинаковы. Математики не смогли вынести такой несправедливости, когда разные функции, имеющие разные графики, словесно описываются одинаково. Они обнаружили принципиальные различия в характере графиков, заметив, что график функции 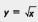 обращен выпуклостью вверх, тогда как
обращен выпуклостью вверх, тогда как
график функции у = х2, где х 0, обращен выпуклостью вниз.
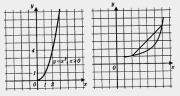
Обычно говорят, что функция выпукла вниз, если, соединив любые две точки ее графика отрезком прямой, обнаруживают, что соответствующая часть графика лежит ниже проведенного отрезка (рис. 81); функция выпукла вверх, если, соединив любые две точки ее графика отрезком прямой, обнаруживают, что соответствующая часть графика лежит выше проведенного отрезка. Свойство выпуклости будем в дальнейшем включать в процедуру чтения графика.
Функция у = f (х)у где f (х) = , принимает любые неотрицательные значения. В самом деле, какое бы конкретное значение у 0 ни задать, всегда найдется такое х, что выполняется равенство f (х) = у, т.е.
, принимает любые неотрицательные значения. В самом деле, какое бы конкретное значение у 0 ни задать, всегда найдется такое х, что выполняется равенство f (х) = у, т.е.  = у; для этого достаточно положить х = у2. Множество всех значений функции называют обычно областью значений функции. Для функции у =
= у; для этого достаточно положить х = у2. Множество всех значений функции называют обычно областью значений функции. Для функции у = областью значения значений является луч [0, + оо). Это, кстати, хорошо читается по графику функции (рис. 79). Если спроецировать график на ось у, как раз и получится луч [0, + оо ).
областью значения значений является луч [0, + оо). Это, кстати, хорошо читается по графику функции (рис. 79). Если спроецировать график на ось у, как раз и получится луч [0, + оо ).
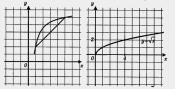
Пример 1. Найти наименьшее и наибольшее значения функции у =  на отрезке:
на отрезке:
а) [0, 4]; б) [1, 5].
Решение, а) Построим график функции у =  и выделим его часть на отрезке [0, 4] (рис. 83). Замечаем, что Унаим. = 0 (достигается при х = 0), а унаи6 = 2 (достигается при х = 4).
и выделим его часть на отрезке [0, 4] (рис. 83). Замечаем, что Унаим. = 0 (достигается при х = 0), а унаи6 = 2 (достигается при х = 4).
б) Построим график функции у =  и выделим его часть на отрезке [1, 5] (рис. 84). Замечаем, что унаим = 1 (достигается при х = 1), а унаиб =
и выделим его часть на отрезке [1, 5] (рис. 84). Замечаем, что унаим = 1 (достигается при х = 1), а унаиб = 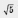 (достигается при х = 5).
(достигается при х = 5).
О т в е т: а) унаим. = 0; унаиб = 2; б) унаим. = 1; ушиб = 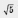
Пример 2. Решить уравнение  = 6 - х.
= 6 - х.
Решение.
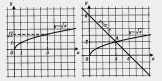
1) Рассмотрим две функции у = 6 - x и y = 
2) Построим график функции у =  (рис. 85).
(рис. 85).
3) Построим график линейной функции у = 6 - х.
Это — прямая, которую можно построить по двум точкам (0; 6) и (6; 0). Прямая изображена на том же чертеже (рис. 85).
4) По чертежу устанавливаем, что графики пересекаются в одной точке А (4; 2). Так ли это на самом деле? Проверим: пара (4; 2) удовлетворяет и уравнению у =  и уравнению у = 6 - х.
и уравнению у = 6 - х.
Это значит, что точка (4; 2) на самом деле служит точкой пересечения построенных графиков. Заданное уравнение имеет один корень 4 — это абсцисса точки А.
Ответ: 4.
Пример 3. Построить график функции 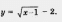
Решение. 1) Перейдем к вспомогательной системе координат с началом в точке (1; -2) (пунктирные прямые х = 1 и у = - 2 на рис. 86).
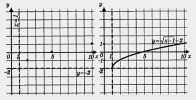
2) Привяжем функцию у =  к новой системе координат.
к новой системе координат.
Для этого выберем контрольные точки для функции у =  . , например (0; 0), (1; 1), (4; 2), (9; 3), но строить их будем не в старой, а в новой системе координат (эти точки отмечены на рис. 86). Построим ветвь параболы, проходящую через выбранные точки, — это и есть требуемый график (рис. 87).
. , например (0; 0), (1; 1), (4; 2), (9; 3), но строить их будем не в старой, а в новой системе координат (эти точки отмечены на рис. 86). Построим ветвь параболы, проходящую через выбранные точки, — это и есть требуемый график (рис. 87).
Пример 4. Построить и прочитать график функции y = - 
Решение. Выше, в § 8, мы заметили, что график функции у = - f (х) получается из графика функции у = f (x) с помощью преобразования симметрии относительно оси х.
Воспользовавшись этим, построим график функции у =  и отобразим его симметрично относительно оси х (рис. 88). Это и будет график функции у = -
и отобразим его симметрично относительно оси х (рис. 88). Это и будет график функции у = -  .
.
Перечислим свойства функции у = -  (по графику):
(по графику):
1. Область определения функции — луч [0, + оо).
2. у = 0 при х = 0; у 0.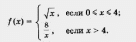
3. Функция убывает на луче [0, + оо).
4. Функция ограничена сверху и не ограничена снизу.
5 Унаиб. = 0 (достигается при х = 0), унаим не существует.
6. Функция непрерывна на луче [0, + од).
7. Область значений функции — луч (- оо, 0].
8. Функция выпукла вниз.
Пример 5. Построить и прочитать график функции y =f(x), где
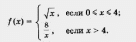
Решение. Сначала построим график функции у =  и выделим его часть на отрезке [0, 4] (рис. 89). Затем построим гиперболу
и выделим его часть на отрезке [0, 4] (рис. 89). Затем построим гиперболу 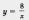 и выделим ее часть на открытом луче (4, + оо) (рис. 90). Наконец, оба «кусочка» изобразим в одной системе координат — это и есть график функции у = f(x) (рис. 91).
и выделим ее часть на открытом луче (4, + оо) (рис. 90). Наконец, оба «кусочка» изобразим в одной системе координат — это и есть график функции у = f(x) (рис. 91).
Перечислим свойства функции у — f(x), т.е. прочитаем график.
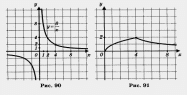
1. Область определения функции — луч [0, + оо).
2. у = 0 при x = 0; у 0 при х 0.
3. Функция возрастает на отрезке [0, 4] и убывает на луче [4, + оо).
4. Функция ограничена и снизу и сверху.
5. Функция непрерывна в заданной области определения.
6. Область значений функции — отрезок [0, 2].
7. Функция выпукла вверх на отрезке [0, 4] и выпукла вниз на луче [4, + оо).
Практические задания
1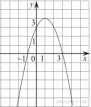 .
.
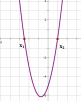
На рисунке изображён график квадратичной функции y = f(x).
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
1) f(x) x
2) Наибольшее значение функции равно 3
3) f(0) f(4)
Если ответов несколько, запишите их в порядке возрастания
2. На рисунке изображены графики функций вида y = ax2 + bx + c. Установите соответствие между графиками функций и знаками коэффициентов a и c.
КОЭФФИЦИЕНТЫ
А) 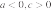
Б) 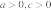
В) 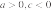
ГРАФИКИ
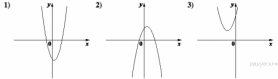
В таблице под каждой буквой укажите соответствующий номер.
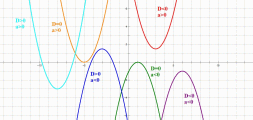
3. Установите соответствие между функциями и их графиками.
ФУНКЦИИ
А) 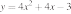
Б) 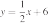
B) 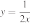
ГРАФИКИ
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
4. Найдите значение  по графику функции
по графику функции 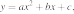 изображенному на рисунке.
изображенному на рисунке.
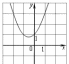
5. На рисунке изображены графики функций вида y = kx + b. Установите соответствие между знаками коэффициентов k и b и графиками функций.
Графики
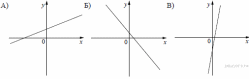
Коэффициенты
| 1) k 0, b | 2) k | 3) k 0 | 4) k 0, b 0 |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
6. Найдите значение  по графику функции
по графику функции 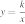 , изображенному на рисунке.
, изображенному на рисунке.
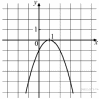
7. На рисунке изображён график функции y = ax2 + bx + c . Установите соответствие между утверждениями и промежутками, на которых эти утверждения выполняются. Впишите в приведённую в ответе таблицу под каждой буквой соответствующую цифру.
| УТВЕРЖДЕНИЯ | | ПРОМЕЖУТКИ |
| А) функция возрастает на промежутке
Б) функция убывает на промежутке | | 1) [1;2] 2) [0;2] 3) [-1;0] 4) [-2;3] |
Ответ:
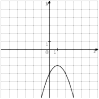
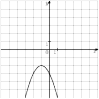
8. На одном из рисунков изображен график функции 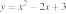 . Укажите номер этого рисунка.
. Укажите номер этого рисунка.
9. На одном из рисунков изображена парабола. Укажите номер этого рисунка.
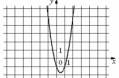
10. На рисунке изображён график функции y = ax2 + bx + c. Установите соответствие между утверждениями и промежутками, на которых эти утверждения выполняются.
| УТВЕРЖДЕНИЯ | | ПРОМЕЖУТКИ |
| А) функция возрастает на промежутке
Б) функция убывает на промежутке | | 1) [2;3] 2) [-2;0] 3) [-3;1] 4) [0;1] |
11. Установите соответствие между функциями и их графиками.
ФУНКЦИИ
А)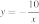
Б)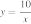
В)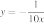
ГРАФИКИ
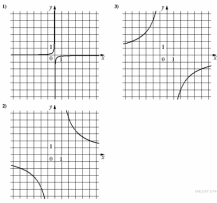
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
12. На рисунке изображены графики функций вида y = ax2 + bx + c. Для каждого графика укажите соответствующее ему значения коэффициента a и дискриминанта D.
Графики
Знаки чисел
| 1) a 0, D 0 | 2) a 0, D | 3) a D 0 | 4) a D |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
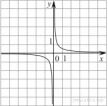
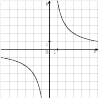
13. На одном из рисунков изображена гипербола. Укажите номер этого рисунка.
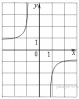
14. На рисунке изображён график функции 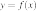 . Какие из утверждений относительно этой функции неверны? Укажите их номера.
. Какие из утверждений относительно этой функции неверны? Укажите их номера.
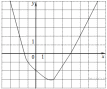
1) функция возрастает на промежутке 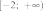
2) 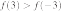
3) 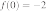
4) прямая  пересекает график в точках
пересекает график в точках 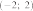 и
и 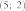
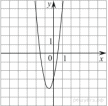
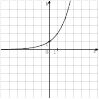
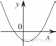
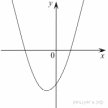
15. График какой из приведенных ниже функций изображен на рисунке?
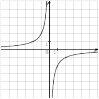
16. На одном из рисунков изображен график функции 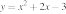 . Укажите номер этого рисунка.
. Укажите номер этого рисунка.
17. На рисунке изображён график функции вида 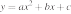 . Установите соответствие между утверждениями и промежутками, на которых эти утверждения выполняются. Впишите в приведённую в ответе таблицу под каждой буквой соответствующую цифру.
. Установите соответствие между утверждениями и промежутками, на которых эти утверждения выполняются. Впишите в приведённую в ответе таблицу под каждой буквой соответствующую цифру.
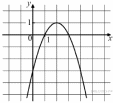
| УТВЕРЖДЕНИЯ | | ПРОМЕЖУТКИ |
| А) функция возрастает на промежутке Б) функция убывает на промежутке | | 1) [0; 3] 2) [−1; 1] 3) [2; 4] 4) [1; 4] |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
18. Найдите значение  по графику функции
по графику функции 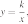 изображенному на рисунке.
изображенному на рисунке.
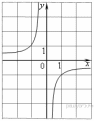
19. Установите соответствие между функциями и их графиками.
Функции
Графики

Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
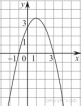
20.
На рисунке изображён график квадратичной функции y = f(x).
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
1) f(−1) = f(3).
2) Наибольшее значение функции равно 3.
3) f(x)0 при −1x
21. На рисунке изображены графики вида 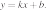 Установите соответствие между графиками функций и знаками коэффициентов k и b.
Установите соответствие между графиками функций и знаками коэффициентов k и b.
Графики
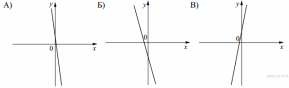
Коэффициенты
| 1) k b 0 | 2) k 0, b 0 | 3) k b |
Ответ:
22. Найдите значение  по графику функции
по графику функции 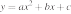 , изображенному на рисунке.
, изображенному на рисунке.
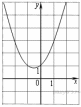
23. Установите соответствие между функциями и их графиками.
Функции
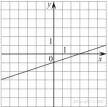
| А) y = −2x + 4 | Б) y = 2x − 4 | В) y= 2x + 4 |
Графики
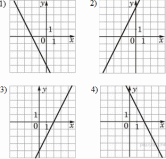
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
24. Установите соответствие между функциями и их графиками.
ФУНКЦИИ
А) 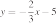
Б) 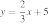
В) 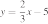
ГРАФИКИ
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
2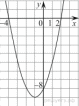 5.
5.
На рисунке изображён график квадратичной функции y=f(x).
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
1) f( −2) = f(2)
2) f(x)0 при xx2
3) Наименьшее значение функции равно −9
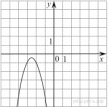
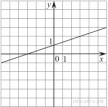
26. Установите соответствие между функциями и их графиками.
ФУНКЦИИ
А)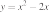
Б)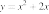
В)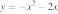
ГРАФИКИ
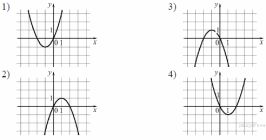
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
27. На рисунке изображён график функции y = ax2 + bx + c . Установите соответствие между утверждениями и промежутками, на которых эти утверждения выполняются.
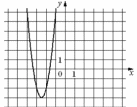
| УТВЕРЖДЕНИЯ | | ПРОМЕЖУТКИ |
| А) функция возрастает на промежутке Б) функция убывает на промежутке | | 1) [-4;-3] 2) [-3;-1] 3) [-3;2] 4) [-2;0] |
28. Установите соответствие между функциями и их графиками.
ФУНКЦИИ
А) 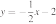
Б) 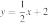
В) 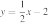
ГРАФИКИ
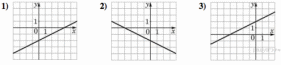
В таблице под каждой буквой укажите соответствующий номер.
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
29. Установите соответствие между графиками функций и формулами, которые их задают.
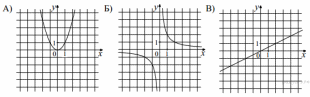
1) 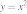
2) 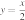
3) 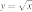
4) 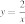
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
30. Найдите значение  по графику функции
по графику функции 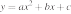 , изображенному на рисунке.
, изображенному на рисунке.
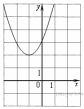
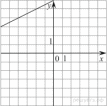
31. Установите соответствие между графиками функций и формулами, которые их задают:
ГРАФИКИ
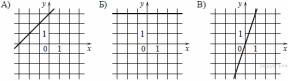
ФОРМУЛЫ
32. Найдите значение  по графику функции
по графику функции 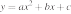 , изображенному на рисунке.
, изображенному на рисунке.

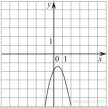
33. Установите соответствие между функциями и их графиками.
ФУНКЦИИ
А) 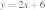
Б) 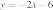
В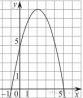 )
) 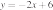
ГРАФИКИ
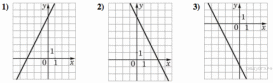
В таблице под каждой буквой укажите соответствующий номер.
34.
На рисунке изображён график квадратичной функции y = f(x).
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
1) Функция возрастает на промежутке [2; +∞)
2) f(x)0 при −1x
3) f(0)f(4)
35. Установите соответствие между функциями и их графиками.
А) 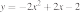
Б) 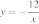
В) 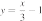
Ответ укажите в виде последовательности цифр без пробелов и запятых в указанном порядке
36. На рисунке изображён график функции y = ax2 + bx + c . Установите соответствие между утверждениями и промежутками, на которых эти утверждения выполняются.
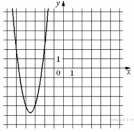
| УТВЕРЖДЕНИЯ | | ПРОМЕЖУТКИ |
| А) функция возрастает на промежутке Б) функция убывает на промежутке | | 1) [-4;3] 2) [1;2] 3) [-4;-3] 4) [-6;-4] |
37. Установите соответствие между функциями и их графиками.
ФУНКЦИИ
А) 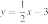
Б) 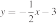
В) 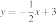
ГРАФИКИ
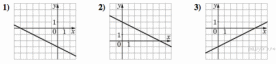
В таблице под каждой буквой укажите соответствующий номер.
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
38. Установите соответствие между функциями и их графиками.
ФУНКЦИИ
А) 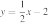
Б) 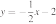
В) 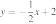
ГРАФИКИ
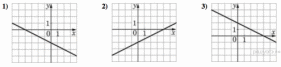 В таблице под каждой буквой укажите соответствующий номер.
В таблице под каждой буквой укажите соответствующий номер.
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
39. Найдите значение  по графику функции
по графику функции 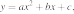 изображенному на рисунке.
изображенному на рисунке.
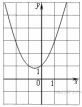
40. На рисунке изображены графики функций вида y = ax2 + bx + c. Установите соответствие между графиками функций и знаками коэффициентов a и c.
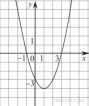
КОЭФФИЦИЕНТЫ
А) 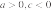
Б) 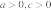
В) 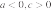
ГРАФИКИ
В таблице под каждой буквой укажите соответствующий номер.
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
41.
На рисунке изображён график квадратичной функции y = f(x).
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
1) Функция возрастает на промежутке [1; +∞).
2) f(−2) = f(2).
3) Наименьшее значение функции равно –4.
42. Установите соответствие между функциями и их графиками.
ФУНКЦИИ
А) 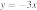
Б) 
B) 
ГРАФИКИ
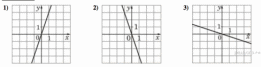
В таблице под каждой буквой укажите соответствующий номер.
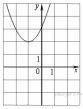
43. Найдите значение  по графику функции
по графику функции 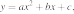 изображенному на рисунке.
изображенному на рисунке.
44. Установите соответствие между функциями и их графиками.
ФУНКЦИИ
А) 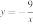
Б) 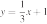
B) 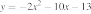
ГРАФИКИ
В таблице под каждой буквой укажите соответствующий номер.
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
45. На рисунке изображён график функции y = ax2 + bx + c . Установите соответствие между утверждениями и промежутками, на которых эти утверждения выполняются.
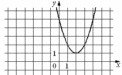
| УТВЕРЖДЕНИЯ | | ПРОМЕЖУТКИ |
| А) функция возрастает на промежутке Б) функция убывает на промежутке | | 1) [1;3] 2) [0;2] 3) [2;4] 4) [-2;3] |
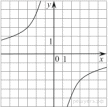
46. На рисунке изображены графики функций вида 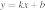 . Установите соответствие между знаками коэффициентов
. Установите соответствие между знаками коэффициентов  и
и  и графиками.
и графиками.
КОЭФФИЦИЕНТЫ
А) 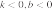
Б) 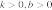
В) 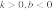
ГРАФИКИ
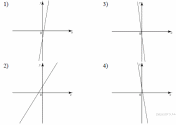
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
47. На одном из рисунков изображен график функции 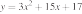 . Укажите номер этого рисунка.
. Укажите номер этого рисунка.
48.
На рисунке изображён график квадратичной функции y=f(x).
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
1) Функция возрастает на промежутке [2; +∞)
2) f( −1 ) f( 5 )
3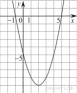 ) Наименьшее значение функции равно −9
) Наименьшее значение функции равно −9
49.
На рисунке изображены графики функций вида y = kx + b. Установите соответствие между графиками функций и знаками коэффициентов k и b.
Графики
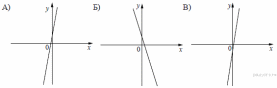
Коэффициенты
| 1) k b 0 | 2) k 0, b 0 | 3) k b | 4) k 0, b |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
5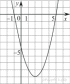 0.
0.
На рисунке изображён график квадратичной функции y = f(x).
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
1) f(x)x
2) Функция возрастает на промежутке [2; +∞).
3) Наименьшее значение функции равно −5.





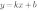
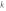 , которое мы умножаем на
, которое мы умножаем на 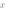 называется коэффициентом наклона.
называется коэффициентом наклона.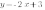
 ;
;
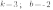 ;
;
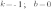 ;
;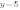
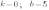 .
. Графиком линейной функции является прямая линия.
Графиком линейной функции является прямая линия.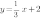 , удобно взять
, удобно взять 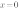 и
и 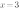 , тогда ординаты эти точек будут равны
, тогда ординаты эти точек будут равны 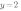 и
и 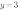 .
.
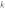 отвечает за наклон графика функции:
отвечает за наклон графика функции: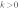
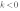
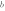 отвечает за сдвиг графика вдоль оси
отвечает за сдвиг графика вдоль оси 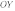 :
: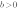
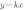 сдвигом на
сдвигом на 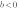
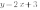 ;
; 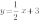 ;
; 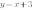

 - и мы видим, что все графики пересекают ось OY в точке (0;3)
- и мы видим, что все графики пересекают ось OY в точке (0;3)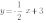 ;
; 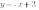

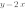 ;
; 





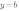 и ее график имеет вид:
и ее график имеет вид:

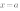 . График этого уравнения представляет собой прямую линию, параллельую оси
. График этого уравнения представляет собой прямую линию, параллельую оси 
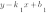 параллелен графику функции
параллелен графику функции  , если
, если 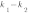
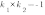 или
или 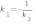
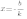 . То есть точка пересечения с осью OX имеет координаты (
. То есть точка пересечения с осью OX имеет координаты (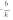 ;0):
;0):
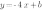
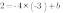 отсюда b=-10
отсюда b=-10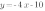

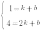
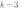 . Подставим значение k в первое уравнение системы, и получим b=-2.
. Подставим значение k в первое уравнение системы, и получим b=-2.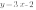 .
.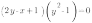
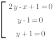


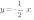 и проходит через точку М(-1;2)
и проходит через точку М(-1;2)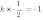 , отсюда
, отсюда 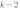 . То есть уравнение функции имеет вид
. То есть уравнение функции имеет вид 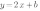
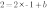 , отсюда
, отсюда  .
.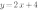 .
.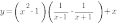
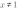
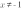
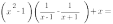
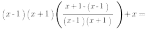
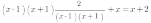
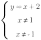
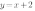 и выколоть на нем две точки: с абсциссами x=1 и x=-1:
и выколоть на нем две точки: с абсциссами x=1 и x=-1:
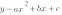 , где
, где 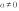
 называется квадратичной функцией.
называется квадратичной функцией.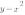 имеет вид:
имеет вид:
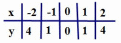
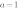 , то график квадратичной функции имеет ровно такую же форму, как график функции
, то график квадратичной функции имеет ровно такую же форму, как график функции 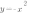 имеет вид:
имеет вид:
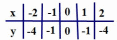
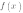 - это точки пересечения графика функции
- это точки пересечения графика функции 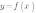 с осью ОХ.
с осью ОХ.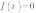 .
.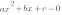 .
.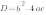 , который определяет число корней квадратного уравнения.
, который определяет число корней квадратного уравнения.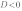
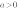

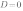

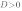
 ,
, 




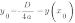
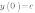 .
.
 ассмотрим несколько способов построения квадратичной параболы. В зависимости от того, каким образом задана квадратичная функция, можно выбрать наиболее удобный.
ассмотрим несколько способов построения квадратичной параболы. В зависимости от того, каким образом задана квадратичная функция, можно выбрать наиболее удобный.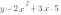
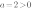

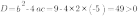
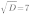
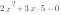
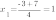 ,
, 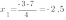
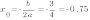
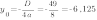


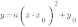 - в этом уравнении
- в этом уравнении 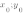 - координаты вершины параболы
- координаты вершины параболы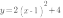 .
.
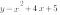 . В уравнении этой функции
. В уравнении этой функции 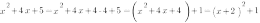
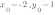 . Старший коэффициент равен 1, поэтому построим по шаблону параболу с вершиной в точке (-2;1):
. Старший коэффициент равен 1, поэтому построим по шаблону параболу с вершиной в точке (-2;1):
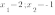
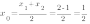
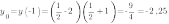





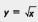 дадим, как обычно, независимой переменной х несколько конкретных значений (неотрицательных, поскольку при х
дадим, как обычно, независимой переменной х несколько конкретных значений (неотрицательных, поскольку при х  не имеет смысла) и вычислим соответствующие значения зависимой переменной у. Разумеется, мы будем давать х такие значения, для которых известно точное значение квадратного корня. Итак:
не имеет смысла) и вычислим соответствующие значения зависимой переменной у. Разумеется, мы будем давать х такие значения, для которых известно точное значение квадратного корня. Итак:

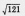 = 11, а 11 10. Возьмем число 40. Найдется ли такое значение х, для которого будет выполняться неравенство
= 11, а 11 10. Возьмем число 40. Найдется ли такое значение х, для которого будет выполняться неравенство 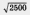 = 50, а 50 40. И вообще, какое бы положительное число т ни взять, всегда найдется такое х, что будет выполняться неравенство
= 50, а 50 40. И вообще, какое бы положительное число т ни взять, всегда найдется такое х, что будет выполняться неравенство 
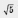 (достигается при х = 5).
(достигается при х = 5). 

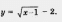

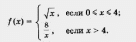
 и выделим ее часть на открытом луче (4, + оо) (рис. 90). Наконец, оба «кусочка» изобразим в одной системе координат — это и есть график функции у = f(x) (рис. 91).
и выделим ее часть на открытом луче (4, + оо) (рис. 90). Наконец, оба «кусочка» изобразим в одной системе координат — это и есть график функции у = f(x) (рис. 91). 
 .
.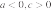
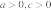
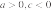

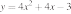
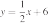
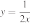
 по графику функции
по графику функции 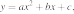 изображенному на рисунке.
изображенному на рисунке.

 по графику функции
по графику функции 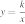 , изображенному на рисунке.
, изображенному на рисунке.


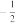


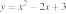 . Укажите номер этого рисунка.
. Укажите номер этого рисунка.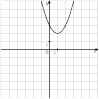




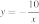
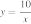
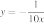





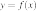 . Какие из утверждений относительно этой функции неверны? Укажите их номера.
. Какие из утверждений относительно этой функции неверны? Укажите их номера.
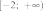
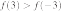
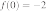
 пересекает график в точках
пересекает график в точках 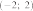 и
и 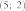
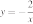
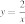
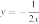
 . Укажите номер этого рисунка.
. Укажите номер этого рисунка.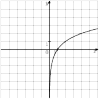

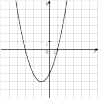
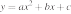 . Установите соответствие между утверждениями и промежутками, на которых эти утверждения выполняются. Впишите в приведённую в ответе таблицу под каждой буквой соответствующую цифру.
. Установите соответствие между утверждениями и промежутками, на которых эти утверждения выполняются. Впишите в приведённую в ответе таблицу под каждой буквой соответствующую цифру.
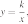 изображенному на рисунке.
изображенному на рисунке.
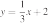
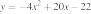
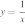


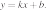 Установите соответствие между графиками функций и знаками коэффициентов k и b.
Установите соответствие между графиками функций и знаками коэффициентов k и b.
 по графику функции
по графику функции 

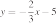
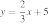
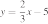
 5.
5.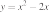
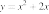
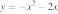
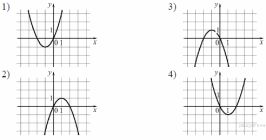

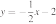
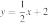
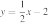


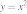






 по графику функции
по графику функции 
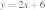
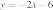
 )
) 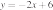

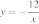
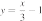

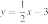
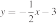

 В таблице под каждой буквой укажите соответствующий номер.
В таблице под каждой буквой укажите соответствующий номер.




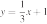
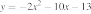

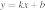 . Установите соответствие между знаками коэффициентов
. Установите соответствие между знаками коэффициентов 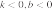
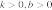
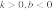

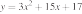 . Укажите номер этого рисунка.
. Укажите номер этого рисунка.
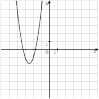

 ) Наименьшее значение функции равно −9
) Наименьшее значение функции равно −9
 0.
0.




















