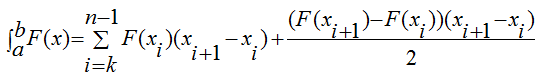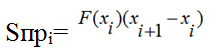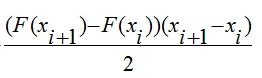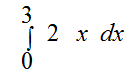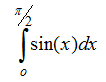16.04.2020 Практическая работа 8

Практическая работа 8

Вычисление интегралов методами численного интегрирования

Для численного вычисления определенного интеграла с использованием конечных разностей существует несколько методов. Наиболее простым является метод трапеций. Для вычисления определенного интеграла по методу трапеций используется формула:

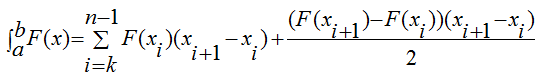
где a и b - пределы интегрирования; n-1 количество равных отрезков, на которые разбит интервал интегрирования, xi - значение аргумента, соответствующее текущему шагу интегрирования i.

Графическая интерпретация этой формулы имеет вид как на рис 1.

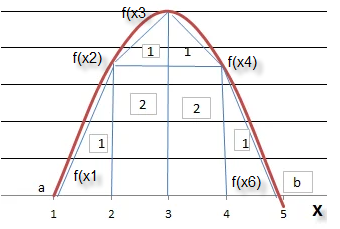
Рис.1.

Весь интервал интегрирования разбивается на одинаковое количество участков (n-1), каждой точке i на интервала разметки соответствует вычисляемое значение функции F(xi). Функция от точки до точки представляется прямым отрезком. Из рисунка видно, что площадь всей фигуры складывается из суммы площадей прямоугольников (2) и треугольников (3). Площадь каждого прямоугольника вычисляется по формуле:

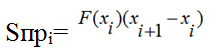
а площадь i-того треугольника равна:

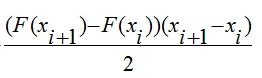
Если вычислить площадь каждой трапеции, изменяя значения I от к до n-1 и затем эти площади просуммировать, то получим приближенное значение интеграла. При этом, чем меньше шаг интегрирования, тем точнее вычисленное значение.

Технология вычисления определенного интеграла в электронной таблице основана на построении табличных значений подинтегрального выражения для каждого шага интегрирования. Используя его можно получить лишь приближенное значение интеграла.

Для численного вычисления величины интеграла в электронной таблице можно применить две технологии – технологию приближенного вычисления и технологию точного вычисления.

Технологию приближенного вычисления определенного интеграла в Excel с использованием формулы трапеций рассмотрим на примере.

Практическая часть

Пример 1. Пусть требуется вычислить определенный интеграл

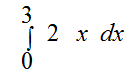
Величина интеграла, вычисленная аналитически, равна 9, проверим путем численного вычисления по методу трапеций.

Решение

Технология приближенного вычисления

1. Табулируем подинтегральную функцию в диапазоне изменения значений аргумента 0 – 3 с шагом 0,2 (рис. 2).

2. В ячейку С2 введем формулу =(A3-A2)*B2+(A3-A2)*(B3-B2)/2, которая реализует часть приведенной выше формулы, размещенной правее знака суммы, т.е вычисляет величину элементарной площадки (криволинейной трапеции).

3. Скопируем буксировкой формулу, записанную в ячейке С2, до значения аргумента х = 2,8.

4. В ячейке С17 просуммируем с помощью автосуммирования полученные результаты. Вычисленное значение в ячейке С17 и будет величиной интеграла - 9.

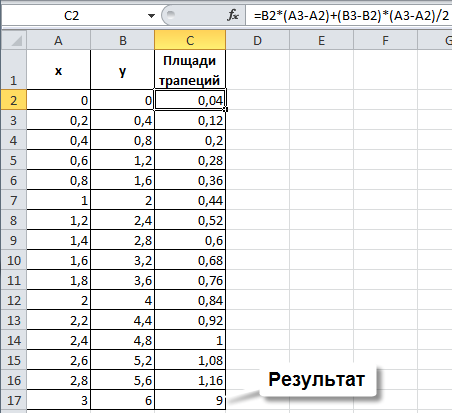
Рис. 2.

Результат получился такой же, как и при аналитическом вычислении, т.е. точный. Это стало возможным, та как подинтеральная функция линейна. В других случаях, когда подинтегральная функция нелинейна, результат может значительно отличаться при таком шаге интегрирования. Если шаг интегрирования значительно уменьшить, таблица (рис. 2) станет очень длинной.

В этом случае можно предложить другу технологию, которая основана на возможности реализации итераций в Excel.

Технология точного вычисления

Технология точного вычисления основана на использовании аппарата циклических ссылок и итераций. Применение этой технологии позволяет задавать достаточно малый шаг интегрирования, что увеличивает точность вычислений. Для точного вычисления нужно выполнить следующие операции:

1. Определить на сколько интервалов нужно разбить диапазон интегрирования, чтобы получить требуемую точность, и задать их количество в виде количества итераций. Положим для решения нашей задачи достаточно 1000 интервалов.

2. Выполним команду меню Файл Параметры, в открывшемся диалоговом окне Параметры Excel параметр Формулы. В правой части окна установим параметры вычислений поле Предельное число итераций введем число 1000 (считаем, что диапазон интегрирования будет разбит на 999 интервалов). Если установлена опция Включить итеративные вычисления, то выключим ее. (Рис. 3).

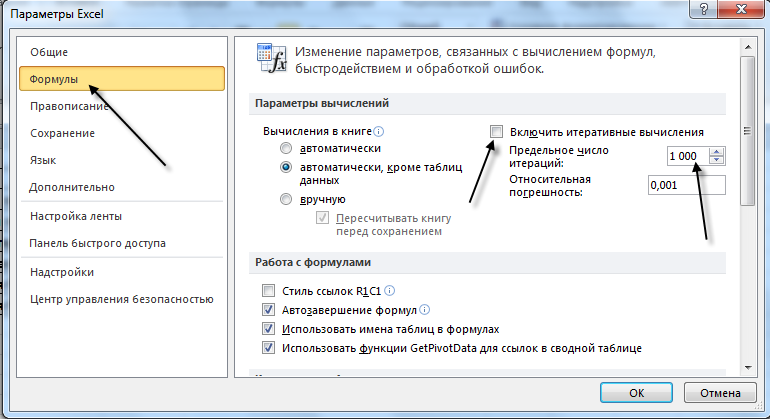
Рис. 3.

3. В ячейки рабочего листа введем исходные данные и формулы для вычислений (рис. 4).

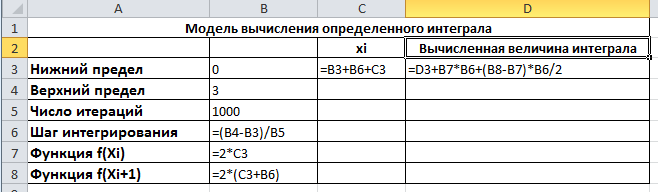
Рис. 4.

В ячейке В6 формула =(B4-B2)/B5 вычисляет шаг интегрирования. В ячейке С3 формула =В3+C3+B6 – вычисляет текущее значение аргумента Xi на i-том шаге итерации . В формуле есть циклическая ссылка на эту же ячейку - С3. Значение в ячейке В3 в формуле устанавливает нижний предел интегрирования, а в В4 - верхний предел.В ячейке В7 вычисляется значение функции на i -том шаге, а в ячейке В8 - на i+1 шаге итерации.

В ячейке D3 записана формула, реализующая метод трапеций и накопление суммы площадей элементарных трапеций.

3. После ввода исходных данных и формул вновь выполним команду меню
Файл Параметры, в открывшемся диалоговом окне Параметры Excel параметр Формулы. Включим опцию Включить итеративные вычисления.

Потребуется некоторое время для того, чтобы табличный процессор выполнил заданное количество циклов итераций и вычислил результат (рис. 5).

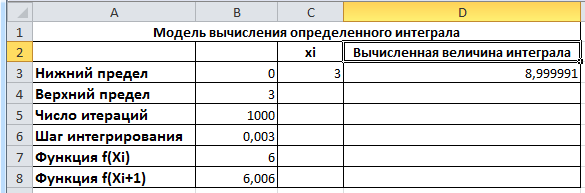
Рис. 5.

4. После завершения вычислений вновь включим диалоговое окно Параметры Excel и выключим опцию Включить итеративные вычисления.

Задания для закрепления

1. Попробуйте самостоятельно вычислить определенный интеграл одним из рассмотренных способов

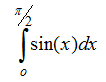
2. Определите стоимость перевозки 20 тонн груза по железной дороге на расстояние 20 км при условии, что тариф перевозки одной тонны груза убывает на 5 рублей на каждом километре. Начальный тариф для первого километра составляет 150 рублей. (Ответ 40000).