Урок № 4
06.04.2020 8-Б класс
Тема: Решение неравенств, содержащих дроби
Цели: разобрать способ решения неравенств с одной переменной, содержащих дроби; продолжить формирование навыков решения неравенств путём перехода к равносильным линейным неравенствам.
1. Актуализация
Продолжаем изучать раздел «Неравенства с одной переменной и их свойства».
Перед изучением нового материала необходимо проверить, насколько хорошо вы усвоили тему предыдущих двух уроков. Для этого необходимо пройти тест по ссылке:
https://multiurok.ru/daria_zhivoglyad/tests/algebra-8-klass-1/
Этот тест находится на сайте Дарьи Владимировны. Перебирайтесь туда, потом обратно, домой.
Тесты составлены по вариантам. Перед прохождением теста повторите решенные примеры.
| 1 вариант | Аверина, Роминская, Зверева, Гущеваров, Ибрагтимов, Доненко, Алаев |
| 2 вариант | Горинов, Балан, Свидлова, Керимов, Терещенко, Иванова, Гармаш. Приходько |
2. ИЗУЧЕНИЕ НОВОГО МАТЕРИАЛА
Сегодня мы с вами научимся решать неравенства, содержащие дроби. На самом деле всё не так страшно, как звучит. От дробных неравенств с помощью равносильных преобразований мы будем переходить к линейным неравенствам, которые уже умеем решать.
Откройте рабочие тетради и запишите сегодняшнее число и тему урока. Далее переписываем алгоритм решения неравенств и примеры.
Алгоритм.
Найти наименьший общий знаменатель дробей.
Умножить обе части неравенства на общий знаменатель.
Решить полученное линейное неравенство.
Пример 1. Решить неравенство 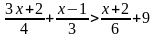 .
.
Начнем применять алгоритм. Наименьший общий знаменатель дробей, входящих в неравенство, равен 12. Поэтому умножим обе части неравенства на положительное число 12(знак неравенства не меняется), получим:
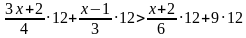
После сокращения получится неравенство
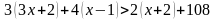
Раскроем скобки
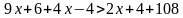
Перенесем в одну часть неизвестные, а в другую - числа
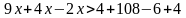
Приведем подобные
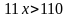
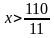
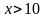

Ответ: 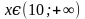 .Обратите внимание на скобки, их вид. Напоминаю, знать название промежутков и их обозначение ОБЯЗАТЕЛЬНО (см таблицу в учебнике)
.Обратите внимание на скобки, их вид. Напоминаю, знать название промежутков и их обозначение ОБЯЗАТЕЛЬНО (см таблицу в учебнике)
Пример 2. Решить неравенство 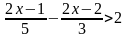 .
.
Алгоритм не меняется. Находим наименьший общий знаменатель, он равен 15, и умножаем обе части неравенства на положительное число 15.
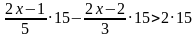
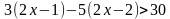
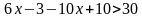
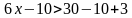
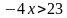
Далее необходимо разделить обе части неравенства на отрицательное число «-4». Знак неравенства поменяется на противоположный.
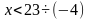
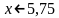

Ответ: 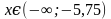 . Вспомни строгие и нестрогие неравенства. Их отличие.
. Вспомни строгие и нестрогие неравенства. Их отличие.
ПРАКТИЧЕСКАЯ ЧАСТЬ. ПРОВЕРЯЕТСЯ
Открываем учебник на странице 192 и выполним письменно №852(б, е). Алгоритм я уже расписывать не буду, его можете посмотреть в лекции.
№ 852. Решите неравенство:
| б) 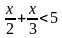 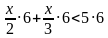
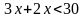
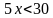
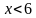
Самостоятельно выполните №852 (г, д)
| Зарисуйте самостоятельно промежуток и запишите ответ. Жду на почту.
Решаем, делаем чертеж. Изображаем промежутки. Записываем ответ.И мне на почту, на проверку. Или фото работы на почту. ЖДУ!!!!!!!!!!! |
3.ПОДВЕДЕНИЕ ИТОГОВ УРОКА. РЕФЛЕКСИЯ
Повторите алгоритм решения неравенства, содержащего дроби.
Домашнее задание: №853(а, б, в) – обязательно для всех,
№854(г, д) – для учащихся, претендующих на 4 и 5.

















