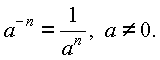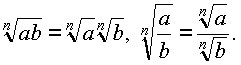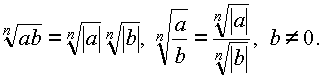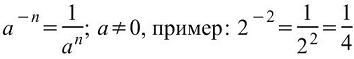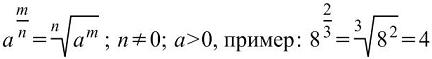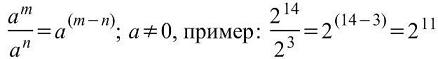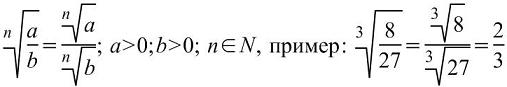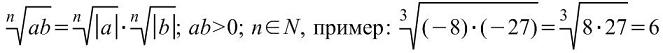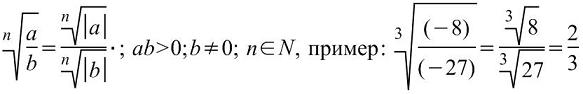СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока

Рабочая тетрадь по математике 1 курс
Методические указания по выполнению практических работ по учебной дисциплине
МАТЕМАТИКА
Перечень практических работ
Название работы Кол-во часов Практическая работа №1 « Приближенные вычисления». 2 Практическая работа №2 «Корни и степени». 2 Практическая работа №3 « Действия над логарифмами». 2 Практическая работа №4 «Преобразование выражений». 2 Практическая работа №5 « Основные тригонометрические тождества». 2 Практическая работа №6 «Решение тригонометрических уравнений». 2 Практическая работа №7 «Решение тригонометрических неравенств». 2 Практическая работа №8 «Исследование функций и построение графиков». 2 Практическая работа №9 «Вычисление табличных производных , составление уравнений касательной и нормали к графику функции» 2 Практическая работа №10 «Применение производной к исследованию функций и построению графиков». 2
Раздел II. Методические указания по выполнению практических работ ПРАКТИЧЕСКАЯ РАБОТА №1 по учебной дисциплине «Математика» Тема: Приближенные вычисления. Цель: научиться применять теоретические знания приближенного вычисления к решению упражнений. Оборудование: 1) Методическое пособие по выполнению работы 2) Учебник Математика Дадаян А.А. 3) Учебник Математика Башмаков М.И. Ход работы: 1. Повторение теоретического материала. а) точные и приближенные значения величин; б) границы приближенного значения величины; в) абсолютная и относительная погрешности; г) действия над приближенными значениями величин.
2. Работа с учебником А.А. Дадаян «Математика» 1) Рассмотреть решение примера стр.31. 2) Рассмотреть решение примера стр. 33
3. Самостоятельное выполнение задания. Определить: a) десятичные приближения по недостатку и по избытку с точностью 0,1; 0,001; 0,0001 б) приближенное значение суммы и произведения данных чисел; в) приближенное значение величины х и точность этого приближения; г) верхнюю и нижнюю границы, если известно приближенное значение и относительная погрешность в %; д) относительную погрешность, если известна абсолютная;
Вариант 1 Исходные данные a) x=1,116809 b) a=0,01111, b=0,005; c) 1,729 3,207; d) x=0,3771, ex=1%; e) x=32,11511, hx=0,11; Вариант 2 Исходные данные a) x=1,678909 b) a=0,06666, b=10,235; c)3,726 4,789; d) x=0,377766, ex=0,5%; e) x=32,61516, hx=0,11;
Вариант 3 Исходные данные 2 a) x=1,203459 b)a=1,2222, b=0,4065; c)2,292 3,987 d) x=0,3772, ex=21%; e) x=32,21512, h=0,0022; Вариант 4 Исходные данные a) x=1,727809 b) a=2,7777; b=10,305; c) 11,727 12,406 d) x=0,3777, ex=5%; e) x=32,71517, hx=0,0077;
Вариант 5 Исходные данные a) x=1,364909 b) a=0,3333, b=11,4005; c) 7,293 9,555; d) x=0,3773, ex=15%; e) x=32,91513, hx=0,0033; Вариант 6 Исходные данные a) x=1,892509 b) a=0,3488, b=33,4605; c) 3,987 4,223; d) x=0,3778, ex=35%; e) x=32,91515, hx=0,0088;
Вариант 7 Исходные данные a) x=1,405769 b) a=2,07214, b=12,576; c) 4,2914 5,677; d) x=0,4774, ex=12%; e) x=32,41514, hx=0,0044; Вариант 8 Исходные данные a) x=1,987709 b) a=3,07219, b=12,567; c)9,291 10,001; d) x=0,9779, ex=53%; e) x=32,91519, hx=0,0099;
Вариант 9 Исходные данные a) x=1,543609 b) a=3,07215, b=10,1115; c)5,291 7,099; d) x=0,37715, ex=33%; e) x=32,51515, hx=0,0055; Вариант 10 Исходные данные a) x=1,9012350 b) a=20,07210, b=5,205; c) 7,291 9,665; d) x=0,97791, ex=25%; e) x=32,915191, hx=0,0091;
4.Сделать вывод.
ПРАКТИЧЕСКАЯ РАБОТА №2 по учебной дисциплине «Математика» Тема: Корни и степени. Цель: научиться выполнять действия с корнями и степенями. Оборудование: 1) методическое пособие по выполнению работы 2) Учебник Математика ДадаянА.А. 3)Учебник Математика Башмаков М.И. Время выполнения: Повторение теоретического материала – 12 минут, решение по образцу – 18 минут, самостоятельное выполнение заданий – 60 минут.
Ход работы: 1. Повторение теоретического материала. ПРАВИЛА ДЕЙСТВИЙ СО СТЕПЕНЯМИ
ПРАВИЛА ДЕЙСТВИЯ С РАДИКАЛАМИ. Пусть m,n,k N, m,n>1;a,b . Тогда:
1. 4. 2. 5. 3. 6. 2. Примеры выполнения заданий.
2. Самостоятельное выполнение задания.
Вариант № 1 1. Упростите 2. Вычислите 3. Упростите 4. Вычислите 5. Упростите 6. Найдите значение выражения , при b= 7. Найдите значение выражения , при a=625, b=16
8. Упростите
9. Упростите 10. Упростите
11. Вычислите 12. Вычислите 13. Вычислите 14. Вычислите 15. Найдите значение выражения , при
Вариант № 2 1. Упростите 2. Вычислите
3. Упростите 4. Вычислите 5. Упростите 6. Найдите значение выражения ,при 7. Найдите значение выражения , если
8. Вычислить при х = 216, у = 27.
9. Упростите
10. Упростите
11. Вычислите 12. Вычислите 13. Вычислите 14. Вычислите 15. Найдите значение выражения , при y=5 4.Сделать вывод
ПРАКТИЧЕСКАЯ РАБОТА №3 по учебной дисциплине «Математика» Тема: Действия над логарифмами. Цель: Научиться применять правила действий с логарифмами. Оборудование: 1) методическое пособие по выполнению работы 2) Учебник Математика ДадаянА.А. 3)Учебник Математика Башмаков М.И. Время выполнения: Повторение теоретического материала – 12 минут, решение по образцу – 18 минут, самостоятельное выполнение заданий – 60 минут. Ход работы: 1. Повторение теоретического материала
Определение. Логарифмом положительного числа b (b>0) по основанию a (a>0, a не равно 1) называется показатель степени, в которую надо возвести a, чтобы получить b.
Обозначение. logab
Основное логарифмическое тождество. b>0 a>0
Свойства и формулы логарифмирования (a>0; ; x>0; y>0)
1. loga1=0 Логарифм единицы по любому основанию равен нулю 2. logaa=1 3. loga(xy)= logax + logay Логарифм произведения положительных чисел равен сумме логарифмов множителей 4. Логарифм частного положительных чисел равен разности логарифмов делимого и делителя 5. Логарифм степени положительного числа равен произведению показателя степени на логарифм основания этой степени.
Формулы перехода от одного основания логарифма к другому.
( ) 2. Примеры выполнения заданий. Задание. Вычислить , если Решение. Перепишем данное выражение, используя свойство логарифма степени и логарифма произведения: Ответ. •Пример. 82log83 = (82log83)2 = 32 = 9 • Логарифм произведения равен сумме логарифмов loga (bc) = logab + logac Пример. log38,1 + log310 = log3 (8,1*10) = log381 = 4 • Логарифм частного равен разности логарифмов loga (b/c) = logab - logac Пример. 9 log550/9 log52 = 9 log550- log52 = 9 log525 = 9 2 = 81 •Свойства степени логарифмируемого числа и основания логарифма Показатель степени логарифмируемого числа logab m = mlogab Показатель степени основания логарифма loganb =1/n*logab loganb m = m/n*logab, если m = n, получим loganb n = logab Пример. log49 = log223 2 = log23 • Переход к новому основанию logab = logcb/logca, если c = b, получим logbb = 1 тогда logab = 1/logba Пример. log0,83*log31,25 = log0,83*log0,81,25/log0,83 = log0,81,25 = log4/55/4 = -1
3. Самостоятельное выполнение задания.
Задания. Вариант 1. 1. Вычислите. 2. Найдите значение выражения 3. Вычислите 4. Выполните действие 5. Сократите дробь 6. Вычислите 7. Найдите , если 8. Найдите число а по его логарифму :
Вариант 2. 1. Вычислите 2. Найдите значение выражения 3. Вычислите 4. Выполните действие 5. Сократите дробь 6. Вычислите 7. Известно, что . Найдите 8. Найдите число b по его логарифму
Вариант 3. 1. Вычислите 2. Найдите значение выражения 3. Выполните действие 4. Сократите дробь 5. Вычислите 6. Вычислите 7. Известно, что . Найдите 8. Найдите число k по его логарифму
Вариант 4. 1. Вычислите 2. Найдите значение выражения 3. Вычислите 4. Выполните действие 5. Сократите дробь 6. Вычислите 7. Известно, что . Найдите 8. Найдите число х по его логарифму :
Вариант 5 1.Вычислите 2. Найдите значение выражения 3. Вычислите 4. Выполните действие 5. Вычислите 6. Известно, что . Найдите 7. Найдите значение выражения 8. Найдите число x , если
Вариант 6 1. Вычислите 2. Найдите значение выражения 3. Вычислите 4. Найдите значение выражения 5. Вычислите 6. Известно, что . Найдите 7. Сократите дробь 8. Найдите число k по его логарифму 4. Сделать вывод ПРАКТИЧЕСКАЯ РАБОТА №4 по учебной дисциплине «Математика» Тема: Преобразование выражений. Цель: Научиться преобразовывать выражения, содержащие степени, корни, применять тождества сокращенного умножения. Оборудование: 1) методическое пособие по выполнению работы 2) Учебник Математика ДадаянА.А. 3) Учебник Математика Башмаков М.И. Время выполнения: Повторение теоретического материала – 12 минут, решение по образцу – 18 минут, самостоятельное выполнение заданий – 60 минут. Ход работы: 1. Повторение теоретического материала. Преобразование алгебраических выражений: первый этап их изучения — числа, переменные, степени («цифры»); второй этап их изучения — одночлены («натуральные числа»); третий этап их изучения — многочлены («целые числа»); четвертый этап их изучения — алгебраические дроби («рациональные числа»). При этом каждый следующий этап как бы вбирает в себя предыдущий: так, числа, переменные, степени — частные случаи одночленов; одночлены — частные •случаи многочленов; многочлены — частные случаи алгебраических дробей. Между прочим, в алгебре используют иногда и такие термины: многочлен — целое выражение, алгебраическая дробь — дробное выражение (это лишь усиливает аналогию). Вы знаете, что любое числовое выражение после выполнения всех входящих в его состав арифметических действий принимает конкретное числовое значение — рациональное число (разумеется, оно может оказаться и натуральным числом, и целым числом, и дробью — это неважно). Точно так же любое алгебраическое выражение, составленное из чисел и переменных с помощью арифметических операций и возведения в натуральную степень, после выполнения преобразований принимает вид алгебраической дроби и опять-таки, в частности, может получиться не дробь, а многочлен или даже одночлен). Для таких выражений в алгебре используют термин рациональное выражение. Пример. Доказать тождество
Решение. Доказать тождество — это значит установить, что при всех допустимых значениях переменных его левая и правая части представляют собой тождественно равные выражения. В алгебре тождества доказывают различными способами: 1) выполняют преобразования левой части и получают в итоге правую часть; 2) выполняют преобразования правой части и получают в итоге левую часть; 3) по отдельности преобразуют правую и левую части и получают и в первом и во втором случае одно и то же выражение; 4) составляют разность левой и правой частей и в результате ее преобразований получают нуль. Какой способ выбрать — зависит от конкретного вида тождества, которое вам предлагается доказать. В данном примере целесообразно выбрать первый способ. Для преобразования рациональных выражений принят тот же порядок действий, что и для преобразования числовых выражений. Это значит, что сначала выполняют действия в скобках, затем действия второй ступени (умножение, деление, возведение в степень), затем действия первой ступени (сложение, вычитание). Выполним преобразования по действиям:
Как видите, нам удалось преобразовать левую часть проверяемого тождества к виду правой части. Это значит, что тождество доказано. Однако напомним, что тождество справедливо лишь для допустимых значений переменных. Таковыми в данном примере являются любые значения а и b, кроме тех, которые обращают знаменатели дробей в нуль. Значит, допустимыми являются любые пары чисел (а; b), кроме тех, при которых выполняется хотя бы одно из равенств:
2а - b = 0, 2а + b = 0, b = 0. Преобразование степенных выражений: 1. Применение определения и свойств степени с натуральным показателем. 2. Применение определения и свойств степени с целым показателем. 3. Применение определения и свойств степени с рациональным показателем. 4. Применение определения и свойств степени с действительным показателем. II. Преобразования иррациональных выражений: 1. Применение определения и свойств арифметического квадратного корня. 2. Применение определения и свойств корня n – ой степени. 3. Вынесение множителя из-под знака корня и внесение множителя под знак корня. 4. Сокращение дробей. 5. Освобождение от иррациональности. 6. Применение формул сокращенного умножения для упрощения иррациональных выражений. III. Преобразование тригонометрических выражений: 1. Применение определений понятий синус, косинус, тангенс, котангенс произвольного угла. 2. Применение определения понятия радианная мера угла. 3. Применение основных тригонометрических тождеств. 4. Применение формул привидения. 5. Применение формул синус, косинус, тангенс суммы двух произвольных углов. 6. Применение формул синус, косинус, тангенс суммы двойного угла. IV. Преобразование логарифмических выражений: 1. Применение определения понятия логарифм числа. 2. Применение свойств логарифмов (произведения, частного, степени). 3. Применение определения десятичного логарифма, натурального логарифма, числа е.
2. Примеры выполнения заданий Рассмотрим несколько примеров. Пример 1. Упростить выражение: √(16*a^4/4b^6); Решение: √(16*a^4/4b^6) =√(16*a^4)/ √(4b^6) = 4*a^2/2*b^3. Ответ: √(16*a^4/4b^6) = 4*a^2/2*b^3;
Пример 2. Вынести множитель из-под знака квадратного корня: √(9*a^7*b^3); Решение: √(9*a^7*b^3) = √(9*a^6*a*b^2*b)= √9*√a^6*√a*√b^2*√b = 3*a^3*b*√(a*b); Ответ: √(9*a^7*b^3) = 3*a^3*b*√(a*b); Пример 3. Внести множитель под знак квадратного корня: (3*a*√b)/( √ (3*a)); Решение: (3*a*√b)/ √(3*a) = ((√(9*a^2) )*(√b))/ √(3*a) = √((9*a^2*b)/3*a)= √(3*a*b); Ответ: (3*a*√b)/ √(3*a) = √(3*a*b); Пример 1. . Данное выражение имеет смысл при . Учитывая свойства корней, вынесем множители из – под знака корня. Получим: = = = = = . Пример 2. Упростим выражение . Выполним упрощение с помощью формулы сокращенного умножения. Получим: = = 4-х. ( при условии х . Пример 3. Преобразуем выражение: . Умножим каждый член первого выражения на каждый член второго выражения подобно произведению многочленов. Получим: = = = 108-8 = 100. С другой стороны, есть второй способ решения. Из первой скобки вынести общий множитель 4. Получим . Далее применим формулу разность квадратов: = 4(27-2) = 100. Пример 4. Сократите дробь . Представим , 5 = . Тогда числитель дроби можно разложить на множители, используя формулу разности квадратов. Получаем: = = . Пример 5. Сократите дробь . Разложим на множители числитель дроби, используя формулу разности квадратов, и знаменатель дроби, используя формулу квадрата разности. Получаем: . 3. Самостоятельное выполнение заданий
Вариант 1 1. Вычислить: 2. Найдите значение выражения при .
3. Найдите значение выражения при . 4. Упростить: 5. Вычислите: (2log27)log725 6. Найдите значение выражения при x=81.
------------------------------------------------------------------------------------ Вариант 2 1. Вычислить: 2. Найдите значение выражения при . 3. Найдите значение выражения при . 4. Упростить: 5. Вычислить log464-log5(1/5)+log13 , 6. Найдите значение выражения при =4, =5. --------------------------------------------------------------------- Вариант 3. 1. Вычислить: 2. Найдите значение выражения при . 3. Найдите значение выражения при . 4. Упростить: 5. Вычислить log2 32-log3(1/27)-log32 , 6. Найдите значение выражения: при а = 17 и b = 51 Вариант 4 1. Вычислить: 2. Найдите значение выражения при . 3. Найдите значение выражения при . 4. Упростить: 5. Вычислить log5125+log4(1/64)-log17 , 6. Найти значение выражения при х = 144 и y = 27 ----------------------------------------------------------------------------- Вариант 5 1. Вычислить: 2. Найдите значение выражения при . 3. Найдите значение выражения при . 4. Упростить: 5. Вычислить log 7 49-log 1/6(36)+log131 , 6. Найдите значение выражения при а = 25 и b = 35 ------------------------------------------------------------------------- Вариант 6 1. Вычислить: 2. Найдите значение выражения при . 3. Найдите значение выражения при . 4. Упростить: 5. Вычислить log564:log54 6. Найдите значение выражения , если x=4 , y=25. 4. Сделайте вывод.
ПРАКТИЧЕСКАЯ РАБОТА №5 по учебной дисциплине «Математика» Тема: Основные тригонометрические тождества. Цель: Научиться применять тригонометрические тождества для преобразования выражений. Оборудование: 1) Методическое пособие по выполнению работы 2) Учебник Математика ДадаянА.А. 3)Учебник Математика Башмаков М.И. Время выполнения: Повторение теоретического материала – 12 минут, решение по образцу – 18 минут, самостоятельное выполнение заданий – 60 минут. Ход работы: 1. Повторение теоретического материала. Основные тригонометрические тождества Синус, косинус, тангенс суммы и разности Синус, косинус, тангенс двойного угла. 2. Примеры выполнения заданий Задача Найдите sin α, если известно следующее: Решение Нам известен косинус, но неизвестен синус. Основное тригонометрическое тождество (в «чистом» виде) связывает как раз эти функции, поэтому будем работать с ним. Имеем: sin2 α + cos2 α = 1 ⇒ sin2 α + 99/100 = 1 ⇒ sin2 α = 1/100 ⇒ sin α = ±1/10 = ±0,1. Для решения задачи осталось найти знак синуса. Поскольку угол α ∈ (π/2; π), то в градусной мере это записывается так: α ∈ (90°; 180°). Следовательно, угол α лежит во II координатной четверти — все синусы там положительны. Поэтому sin α = 0,1. Ответ: 0,1 Задача Найдите cos α, если известно следующее: Решение Итак, нам известен синус, а надо найти косинус. Обе эти функции есть в основном тригонометрическом тождестве. Подставляем: sin2 α + cos2 α = 1 ⇒ 3/4 + cos2 α = 1 ⇒ cos2 α = 1/4 ⇒ cos α = ±1/2 = ±0,5. Осталось разобраться со знаком перед дробью. Что выбрать: плюс или минус? По условию, угол α принадлежит промежутку (π 3π/2). Переведем углы из радианной меры в градусную — получим: α ∈ (180°; 270°). Очевидно, это III координатная четверть, где все косинусы отрицательны. Поэтому cos α = −0,5. Ответ: −0,5 Задача Найдите tg α, если известно следующее: Решение Тангенс и косинус связаны уравнением, следующим из основного тригонометрического тождества: Получаем: tg α = ±3. Знак тангенса определяем по углу α. Известно, что α ∈ (3π/2; 2π). Переведем углы из радианной меры в градусную — получим α ∈ (270°; 360°). Очевидно, это IV координатная четверть, где все тангенсы отрицательны. Поэтому tg α = −3. Ответ: −3 Задача Найдите cos α, если известно следующее: Решение Снова известен синус и неизвестен косинус. Запишем основное тригонометрическое тождество: sin2 α + cos2 α = 1 ⇒ 0,64 + cos2 α = 1 ⇒ cos2 α = 0,36 ⇒ cos α = ±0,6. Знак определяем по углу. Имеем: α ∈ (3π/2; 2π). Переведем углы из градусной меры в радианную: α ∈ (270°; 360°) — это IV координатная четверть, косинусы там положительны. Следовательно, cos α = 0,6. Ответ: 0,6 Задача Найдите sin α, если известно следующее: Решение Запишем формулу, которая следует из основного тригонометрического тождества и напрямую связывает синус и котангенс: Отсюда получаем, что sin2 α = 1/25, т.е. sin α = ±1/5 = ±0,2. Известно, что угол α ∈ (0; π/2). В градусной мере это записывается так: α ∈ (0°; 90°) — I координатная четверть. Итак, угол находится в I координатной четверти — все тригонометрические функции там положительны, поэтому sin α = 0,2. Ответ: 0,2 3. Самостоятельное выполнение задания.
Вариант №1
1.Определите знак выражения: cos 7000 tg 3800, cos 3180 ∙ tg (−2140). 2.Найдите cos 2a, tg a, если известно, что sin a=1/5, π/2≤a≤ π. 3.Упростите выражение 4.Вычислить 5. Докажите тождество sin4a + 2sin2a cos2a + cos4a + sin2a + cos2a = 2.
Вариант №2
1. Определите знак выражения: sin 2000 ctg 3400, cos 2850 ∙ cos (−3160) 2. Найдите ctg a , sin 2a, , если известно, что cos a= , 3 π /2≤a≤2 π. 3. Упростите выражение 4. Вычислить 5. Докажите тождество (sin4a - 2sin2a cos2a + cos4a) : (sin a + cos a)2 = 1 - sin2a.
Вариант №3
1. Определите знак выражения: cos 5000 ctg 8000, sin 3 ∙ cos 4 ∙ tg 5 2. Найдите cos 2a, tg a, , если известно, что sin a = - 0,8 , 1800≤a≤2700. 3. Упростите выражение 4. Вычислить 5.Докажите тождество (sin4a + sin2a cos2a) : cos2 a = 1/ cos2 a - 1.
Вариант №4
1. Найдите sin 2a, tg a, , если известно, что cos a= - 24/25, 900≤a≤1800. 2. Определите знак выражения: sin 4600 tg 6000, cos 2850 ∙ cos (−3160) 3. Упростите 4. Вычислите 5. Докажите тождество
Вариант №5
1. Найдите ctg a , cos 2a, если известно, что cos a= - , π /2 ≤a≤ π. 2. Упростите 3. Определите знак выражения: tg 2500 ctg 1000, sin 1000 ∙ sin 1320 4. Вычислить 5. Докажите тождество
Вариант №6
1. Найдите sin a , sin 2a, ctg a, если известно, что tg a= - 3, 3 π /2≤a≤2 π. 2. Упростите 3. Определите знак выражения: cos 7000 tg 9600, sin (−2800) sin (−3) 4. Вычислить 5. Докажите тождество (tg a – sin a)(cos2 a/sina + ctg a) = sin2 a. 4. Сделайте вывод
ПРАКТИЧЕСКАЯ РАБОТА №6 по учебной дисциплине «Математика» Тема: Решение тригонометрических уравнений. Цель: Научиться решать тригонометрические уравнения. Оборудование: 1 )Методическое пособие по выполнению работы 2) Учебник Математика ДадаянА.А. 3)Учебник Математика Башмаков М.И. Время выполнения: Повторение теоретического материала – 12 минут, решение по образцу – 18 минут, самостоятельное выполнение заданий – 60 минут. Ход работы: 1. Повторение теоретического материала. Значения тригонометрических функций некоторых углов.
x 0 1 -1 arcsin x 0 - arсcos x 0
x 0 1 arctg x 0 arcctg x
Формулы для решения простейших тригонометрических уравнений.
sin x = a ; | a | ; x=(-1)n arcsin a + n, n Z; sin x =0; x= k, k Z; sin x = 1; x= +2 k; k Z; sin x = -1 ; x= - + 2 k; k Z;
cos x = a ; |a| ; x= arcos a +2 n, n Z; cos x = 0; x = + k; k Z; cos x = 1 ; x = 2 k; k Z; cos x = -1 ; x = +2 k; k Z;
tg x = a ; x = arctg a + n; n Z; ctg x = a; x = arcctg a + n; n Z. 2. Примеры выполнения заданий . 1) Решить уравнение 2 cos 2 x +sin x + 1 =0 Как представим cos 2 x? Какое уравнение получается? 2(1- sin 2 x) + sin x + 1=0 2- 2 sin 2 x +sin x + 1 =0 Приведём подобные. - 2 sin 2 x + sin x + 3 = 0 | -1 Умножим на –1. 2 sin 2 x – sin x – 3 =0 sin x = y 2 y 2 – y – 3 = 0 D=1+24=25>0 => два корня. y 1 = (1+5)/4 = 6/4 = 3/2; y 2 = (1-5)/4= - 1. Мы получили два уравнения: sin x =3/2 ; sin x =1; E (sin x )=[-1;1 ] x =(-1)karcsin(-1) +Пk, k Z; Корней нет; x =(-1)k * (- П/2 ) + Пk, k Z; или x =(-1)k * 3П/2 + Пk, k Z; Ответ: x =(-1)k * 3П/2 + Пk, k Z;
2) Решить уравнение 6 cos 2 x + cos x – 1 = 0 cos x = y; 6y 2 + y – 1 = 0; D = 1+24=25>0, два корня. y 1= (- 1+5)/12=1/3; y 2 = (-1+5)/12=-6/12= - 1/2 cos x = 1/3; cos x = - 1/ 2 x1 = ± arccos 1/3 + 2 Пk;k Z; x 2 = ± arccos(-1/2) +2 Пk; k Z; x 2 = ± 2П/3 + 2Пk, k Z; Ответ: x1 = ± arccos 1/3 + 2 Пk; k Z; x2 = ± 2П/3 + 2Пk, k Z;
2. Самостоятельное выполнение задания.
Вариант 1 1. Вычислите: arcsin (- ) + 2arcctg (- ) – arctg 1. 2. Решите уравнения: 1) sinх = , 2) cosх = , 3) tgх= , 4) ctgх=1, 5) sinх = - , 6) cosх = -1, 7) tgх=- , 8) ctgх=- . 3.* Решить уравнения: 1) sin 4x = , 2) tg (x- ) = , 3) ctgx (2-cosx)=0. 4) cos2x – sin2 x = - , 5) sin 3x cos(x+ ) + cos 3x sin(x+ ) = 0. 6) 2 sin2 x - 5 sin x – 3 = 0, 7) tg x + 2ctgx = 3.
Вариант 2 1. Вычислите: arccos (- ) - 3arctg (- ) + 4 arcctg 1. 2. Решите уравнения: 1) sinх= , 2) cosх=0, 3) tgх=1, 4) ctgх= , 5) sinх=- , 6) cosх=- , 7) tgх=- , 8) ctgх=-1. 3.* Решить уравнения: 1) сos 3x = , 2) ctg (x+ ) = - , 3) tgx (3-sinx)=0. 4) 2cosx sin x = , 5) cos 2x cos(x+ ) + sin 2x sin(x+ ) = 0. 6) 2 сos2 x - cos x – 1 = 0, 7) ctg x + tgx = 2 .
Вариант 3 1. Вычислите: 2arcsin + arcctg (- ) – 2arccos (- 1). 2. Решите уравнения: 1) sinх= , 2) cosх= , 3) tgх= , 4) ctgх= , 5) sinх=-1, 6) cosх=- , 7) tgх=-1, 8) ctgх=0. 3.* Решить уравнения: 1) tg 5x =- , 2) sin (x+ ) = , 3) cosx (6-ctgx)=0. 4) sin2 x - cos2x = , 5) sin 2x cos(x- ) - cos 2x sin(x- ) = 0. 6) 2 sin2 x - 5 sin x +2 = 0, 7) 2tg x + 2ctgx = 5 .
Вариант 4 1. Вычислите: 3arctg (-1) - 5arcctg (- ) + arccos 1. 2. Решите уравнения: 1) sinх=1, 2) cosх= , 3) tgх= , 4) ctgх=1, 5) sinх=- , 6) cosх=- , 7) tgх=0, 8) ctgх=- . 3.* Решить уравнения: 1) ctg 3x = -1, 2) 2cos (x+ ) =1, 3) sinx (2+tgx)=0. 4) sin x cos x =1, 5) cos 4x cos(x+ ) + sin 4x sin(x+ ) = 0. 6) sin2 x - 4 sin x + 3 = 0, 7) 3tg x - 3ctgx = 8.
Вариант 5 1. Вычислите: 5arcsin (- ) + 2arcctg (-1) – arctg 1. 2. Решите уравнения: 1) sinх=0, 2) cosх= , 3) tgх=1, 4) ctgх=0, 5) sinх=- , 6) cosх=- , 7) tgх=- , 8) ctgх=- . 3.* Решить уравнения: 1) sin 7x = - , 2) ctg (x- ) =2, 3) tgx (1-2cosx)=0. 4) 2cos2x – 2sin2 x =1, 5) sin 4x cos(x- ) + cos 4x sin(x- ) = 0. 6) 4 sin2 x - sin x – 3 = 0, 7) 4tg x + 3ctgx = 7 .
Вариант 6 1. Вычислите: arсcos - 2arcctg (- ) +3 arcsin(- 1). 2. Решите уравнения: 1) sinх= , 2) cosх=1, 3) tgх= , 4) ctgх=-1, 5) sinх=- , 6) cosх=0, 7) tgх=- , 8) ctgх=0. 3.* . Решить уравнения: 1) cos 2x = - , 2) ctg ( - x) = , 3) tgx (1-2sinx)=0, 4) cos2x – = sin2 x, 5) sin 2x sin(x+ ) - cos 2x cos(x+ ) = 0. 6) sin2 x - 5 sin x +4 = 0, 7) tg x + 2ctgx = 3 .
ПРАКТИЧЕСКАЯ РАБОТА №7 по учебной дисциплине «Математика» Тема: Решение тригонометрических неравенств. Цель: Научиться решать тригонометрические неравенства. Оборудование: 1) Методическое пособие по выполнению работы 2) Учебник Математика ДадаянА.А. 3) Учебник Математика Башмаков М.И. Время выполнения: Повторение теоретического материала – 12 минут, решение по образцу – 18 минут, самостоятельное выполнение заданий – 60 минут.
Ход работы: 2. Повторение теоретического материала. Значения тригонометрических функций некоторых углов.
x 0 1 -1 arcsin x 0 - arcos x 0
x 0 1 arctg x 0 arcctg x
Формулы для решения простейших тригонометрических неравенств.
sin x < a ; x (arcsin a+2 n; 3 - arcsin a+2 n), n Z sin x >a; x ( arcsin a+2 n; - arcsin a+2 n), n Z cos x< a ; x ( arccos a+2 n; 2 - arcsin a+2 n), n Z cos x > a; x ( -arccos a+2 n; arcsin a+2 n), n Z tg x < a ; x (- ; arctg a + n); n Z; tgx>a; x (arctg a + n; ; ); n Z; ctg x<a ; x ( arcctg a + n; + n);n Z. ctg x>a ; x ( n ;arcctg a + n);n Z. 3. Примеры выполнения заданий .
1) Решить неравенство sin x
Ответ : x
2)Решить неравенство cos x
Ответ: x
4. Самостоятельное выполнение задания. Вариант 1. 1.Решите неравенства: 1) sinх≤1, 2) cosх≥ , 3) tgх≤ , 4) ctgх≥1, 5) sinх≥ , 6) cosх< , 7) tgх >0, 8) ctgх≤ . 2. Определите знак выражения: cos 7000 tg 3800. 3. Найдите cos a , если известно, что sin a=1/5, π/2≤a≤ π. 4. Решите неравенства: 1) sin2х ≥ , 2) cos(х+ )< , 3) tg х< , 4) ctg4х>1, 5) sin( -х )≤ , 6) cos(-3х)≥ 1, 7) tg3х≥ , 8) ctg х≤ .
Вариант 2. 1. Решите неравенства: 1) sinх≥0, 2) cosх< , 3) tgх<1, 4) ctgх>0, 5) sinх≤ , 6) cosх≥ , 7) tgх≥ , 8) ctgх≤ . 2. Определите знак выражения: sin 2000 ctg 3400. 3. Найдите tg a , если известно, что cos a= , 3 π /2≤a≤2 π. 4. Решите неравенства: 1) sin3х≤ , 2) cos(-х)≥1, 3) tg х< , 4) ctg5х≤1, 5) sin( -х)≥ , 6) cos х<0, 7) tg2х≥ , 8) ctg7х>0.
Вариант 3.
1. Решите неравенства: 1) sinх≤ , 2) cosх≥1, 3) tgх< , 4) ctgх≤-1, 5) sinх≥- , 6) cosх<0, 7) tgх≥- , 8) ctgх>0. 2. Определите знак выражения: cos 5000 ctg 8000. 3. Найдите ctg a , если известно, что sin a = - 0,8 , 1800≤a≤2700. 4. Решите неравенства: 1) sin(х+ )≤ , 2) cos2х≥ , 3) tg(-3х)< , 4) ctg2х> , 5) sin х≥1, 6) cos( -х)< , 7) tgх≥-1, 8) ctgх≤0.
Вариант 4.
1. Решите неравенства:
1) sinх ≥ , 2) cosх < , 3) tgх< , 4) ctgх>1, 5) sinх ≤ - , 6) cosх≥ -1, 7) tgх≥- , 8) ctgх≤- . 2. Найдите tg a , если известно, что cos a= - 24/25, 900≤a≤1800. 3. Определите знак выражения: sin 4600 tg 6000. 4. Решите неравенства: 1) sin2х ≥ , 2) cos(х+ )< , 3) tg х< , 4) ctg4х>1, 5) sin( -х )≤ , 6) cos(-3х)≥ 1, 7) tg3х≥ , 8) ctg х≤ .
Вариант 5.
1. Решите неравенства:
1) sinх≥ , 2) cosх<0, 3) tgх≤1, 4) ctgх≥ , 5) sinх≤- , 6) cosх≥- , 7) tgх >- , 8) ctgх≤-1. 2. Найдите tg a , если известно, что cos a= - , π /2 ≤a≤ π. 3. Определите знак выражения: tg 2500 ctg 1000. 4. Решите неравенства: 1) sin3х≤ , 2) cos(-х)≥1, 3) tg х< , 4) ctg5х≤1, 5) sin( -х)≥ , 6) cos х<0, 7) tg2х≥ , 8) ctg7х>0.
Вариант 6. 1. Решите неравенства:
1) sinх≤ , 2) cosх≥ , 3) tgх< , 4) ctgх> , 5) sinх≥-1, 6) cosх<- , 7) tgх≥-1, 8) ctgх≤0. 2. Найдите sin a , если известно, что tg a= - 3, 3 π /2≤a≤2 π. 3. Определите знак выражения: cos 7000 tg 9600. 4. Решите неравенства: 1) sin(х+ )≤ , 2) cos2х≥ , 3) tg(-3х)< , 4) ctg2х> , 5) sin х≥1, 6) cos( -х)< , 7) tgх≥-1, 8) ctgх≤0.
ПРАКТИЧЕСКАЯ РАБОТА №8 по учебной дисциплине «Математика» Тема: Исследование функций и построение графиков. Цель: Научиться исследовать функции и строить их графики. Оборудование: 1) Методическое пособие по выполнению работы 2) Учебник Математика ДадаянА.А. 3)Учебник Математика Башмаков М.И. Время выполнения: Повторение теоретического материала – 12 минут, решение по образцу – 18 минут, самостоятельное выполнение заданий – 60 минут.
Ход работы: 1. Повторение теоретического материала. Схема исследования функции и построение её графика. • Найти область определения функции. • Найти область значений функции. Обычно этот пункт пропускают или заполняют после исследования на экстремумы. • Исследовать непрерывность функции, выделить особые точки (точки разрыва). • Проверить наличие вертикальных асимптот в точках разрыва и на границах области определения. • Найти точки пересечения с осями координат. • Найти нули функции. Найти интервалы знакопостоянства функции. • Установить, является ли функция чётной или нечётной. Сделать выводы о симметричности графика функции. • Установить, является ли функция периодической или нет. Обычно проверяют для тригонометрических функций, для других данный пункт пропускается. • Построить график элементарной функции, а затем способом преобразования графиков построить график данной функции. Способы преобразования графиков. Алгоритм 1. (построение графика функции y = f(x+l) + m )
1. Построить график функции у = f(x). 2. Осуществить параллельный перенос графика у = f(x) вдоль оси х на |l| единиц масштаба влево, если l>0, и вправо, если l<0. 3. Осуществить параллельный перенос полученного на втором шаге графика вдоль оси у на |m| единиц масштаба вверх, если m>0, и вниз, если m<0.
Алгоритм 2. (построение графика функции y = f(x+l) + m )
1. Перейти к вспомогательной системе координат, проведя (пунктиром) вспомогательные прямые x = - l и y = m, т.е. выбрав в качестве начала новой ситемы координат точку ( -l; m ). 2. К новой системе координат привязать график функции у = f(x). Правило: чтобы построить график функции , где , нужно график функции сжать к оси в раз. Правило: чтобы построить график функции , где , нужно график функции растянуть от оси в раз. Правило: чтобы построить график функции , нужно график отобразить симметрично относительно оси . 2.Примеры выполнения заданий. Сжатие графика функции к оси ординат
Пример 1 Построить график функции . Сначала изобразим график синуса, его период равен : К слову, чертить графики тригонометрических функций вручную – занятие кропотливое, поскольку и т.д., то есть на стандартной клетчатой бумаге аккуратным нужно быть вплоть до миллиметра, даже до полумиллиметра. Впрочем, многие с этим уже столкнулись. Мысленно возьмём синусоиду в руки и сожмём её к оси в 2 раза: То есть, график функции получает
Просмотр содержимого документа
«Рабочая тетрадь по математике 1 курс»
| Методические указания по выполнению практических работ по учебной дисциплине
МАТЕМАТИКА
Перечень практических работ
|
Раздел II. Методические указания по выполнению практических работ
ПРАКТИЧЕСКАЯ РАБОТА №1
по учебной дисциплине «Математика»
Тема: Приближенные вычисления.
Цель: научиться применять теоретические знания приближенного вычисления к решению упражнений.
Оборудование: 1) Методическое пособие по выполнению работы
2) Учебник Математика Дадаян А.А.
3) Учебник Математика Башмаков М.И.
Ход работы:
1. Повторение теоретического материала.
а) точные и приближенные значения величин;
б) границы приближенного значения величины;
в) абсолютная и относительная погрешности;
г) действия над приближенными значениями величин.
2. Работа с учебником А.А. Дадаян «Математика»
1) Рассмотреть решение примера стр.31.
2) Рассмотреть решение примера стр. 33
3. Самостоятельное выполнение задания.
Определить:
a) десятичные приближения по недостатку и по избытку с точностью 0,1; 0,001; 0,0001
б) приближенное значение суммы и произведения данных чисел;
в) приближенное значение величины х и точность этого приближения;
г) верхнюю и нижнюю границы, если известно приближенное значение и относительная погрешность в %;
д) относительную погрешность, если известна абсолютная;
| Вариант 1 Исходные данные a) x=1,116809 b) a=0,01111, b=0,005; c) 1,729 d) x=0,3771, ex=1%; e) x=32,11511, hx=0,11;
| Вариант 2 Исходные данные a) x=1,678909 b) a=0,06666, b=10,235; c)3,726 d) x=0,377766, ex=0,5%; e) x=32,61516, hx=0,11;
|
| Вариант 3 Исходные данные 2 a) x=1,203459 b)a=1,2222, b=0,4065; c)2,292 d) x=0,3772, ex=21%; e) x=32,21512, h=0,0022;
| Вариант 4 Исходные данные a) x=1,727809 b) a=2,7777; b=10,305; c) 11,727 d) x=0,3777, ex=5%; e) x=32,71517, hx=0,0077;
|
| Вариант 5 Исходные данные a) x=1,364909 b) a=0,3333, b=11,4005; c) 7,293 d) x=0,3773, ex=15%; e) x=32,91513, hx=0,0033;
| Вариант 6 Исходные данные a) x=1,892509 b) a=0,3488, b=33,4605; c) 3,987 d) x=0,3778, ex=35%; e) x=32,91515, hx=0,0088;
|
| Вариант 7 Исходные данные a) x=1,405769 b) a=2,07214, b=12,576; c) 4,2914 d) x=0,4774, ex=12%; e) x=32,41514, hx=0,0044;
| Вариант 8 Исходные данные a) x=1,987709 b) a=3,07219, b=12,567; c)9,291 d) x=0,9779, ex=53%; e) x=32,91519, hx=0,0099;
|
| Вариант 9 Исходные данные a) x=1,543609 b) a=3,07215, b=10,1115; c)5,291 d) x=0,37715, ex=33%; e) x=32,51515, hx=0,0055;
| Вариант 10 Исходные данные a) x=1,9012350 b) a=20,07210, b=5,205; c) 7,291 d) x=0,97791, ex=25%; e) x=32,915191, hx=0,0091;
|
4.Сделать вывод.
ПРАКТИЧЕСКАЯ РАБОТА №2
по учебной дисциплине «Математика»
Тема: Корни и степени.
Цель: научиться выполнять действия с корнями и степенями.
Оборудование: 1) методическое пособие по выполнению работы
2) Учебник Математика ДадаянА.А.
3)Учебник Математика Башмаков М.И.
Время выполнения: Повторение теоретического материала – 12 минут, решение по образцу – 18 минут, самостоятельное выполнение заданий – 60 минут.
Ход работы:
Повторение теоретического материала.
ПРАВИЛА ДЕЙСТВИЙ СО СТЕПЕНЯМИ
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Правила действия с радикалами.
Пусть m,n,k![]() N, m,n1;a,b
N, m,n1;a,b![]() . Тогда:
. Тогда:
1. ![]() 4.
4. ![]()
2. ![]() 5.
5. ![]()
3. ![]()
![]() 6.
6. ![]()
2. Примеры выполнения заданий.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Самостоятельное выполнение задания.
Вариант № 1
1. Упростите ![]()
2. Вычислите 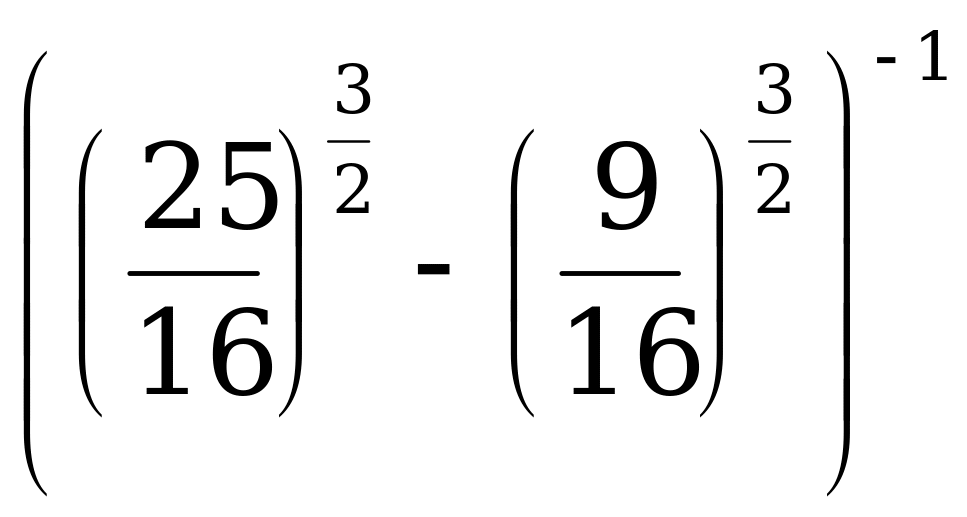
3. Упростите ![]()
4. Вычислите ![]()
5. Упростите ![]()
6. Найдите значение выражения ![]() , при b=
, при b= ![]()
7. Найдите значение выражения 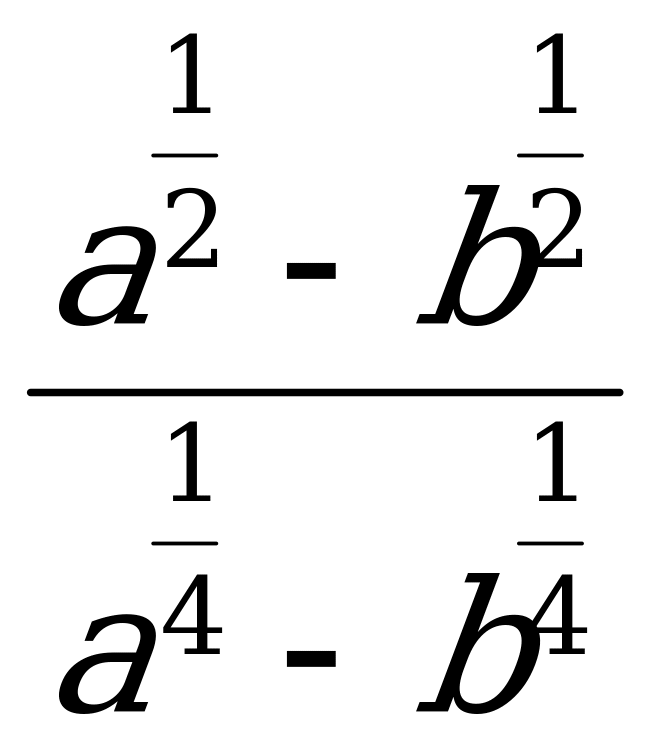 , при
, при ![]() a=625, b=16
a=625, b=16
8. Упростите 
9. Упростите 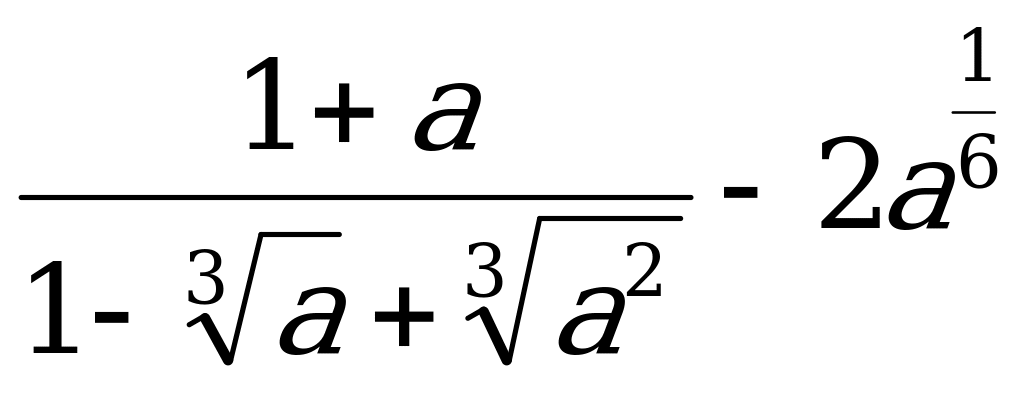
10. Упростите 
11. Вычислите ![]()
12. Вычислите ![]()
13. Вычислите ![]()
14. Вычислите ![]()
15. Найдите значение выражения  , при
, при ![]()
Вариант № 2
1. Упростите ![]()
2. Вычислите ![]()
3. Упростите ![]()
4. Вычислите ![]()
5. Упростите ![]()
6. Найдите значение выражения ![]() ,при
,при ![]()
7. Найдите значение выражения ![]() , если
, если ![]()
8. Вычислить  при х = 216, у = 27.
при х = 216, у = 27.
9. Упростите 
10. Упростите 
11. Вычислите ![]()
12. Вычислите ![]()
13. Вычислите ![]()
14. Вычислите ![]()
15. Найдите значение выражения 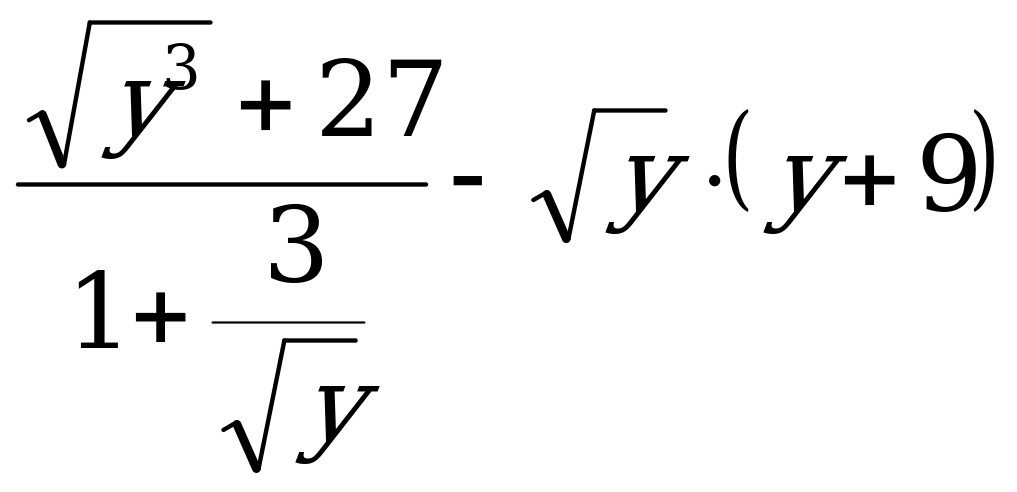 , при y=5
, при y=5
4.Сделать вывод
ПРАКТИЧЕСКАЯ РАБОТА №3
по учебной дисциплине «Математика»
Тема: Действия над логарифмами.
Цель: Научиться применять правила действий с логарифмами.
Оборудование: 1) методическое пособие по выполнению работы
2) Учебник Математика ДадаянА.А.
3)Учебник Математика Башмаков М.И.
Время выполнения: Повторение теоретического материала – 12 минут, решение по образцу – 18 минут, самостоятельное выполнение заданий – 60 минут.
Ход работы:
1. Повторение теоретического материала
Определение. Логарифмом положительного числа b (b0) по основанию a (a0, a не равно 1) называется показатель степени, в которую надо возвести a, чтобы получить b.
Обозначение. logab
Основное логарифмическое тождество.
![]() b0
b0
a0
![]()
Свойства и формулы логарифмирования (a0; ![]() ; x0; y0)
; x0; y0)
| 1. loga1=0 | Логарифм единицы по любому основанию равен нулю |
| 2. logaa=1 |
|
| 3. loga(xy)= logax + logay | Логарифм произведения положительных чисел равен сумме логарифмов множителей |
| 4. | Логарифм частного положительных чисел равен разности логарифмов делимого и делителя |
| 5. | Логарифм степени положительного числа равен произведению показателя степени на логарифм основания этой степени. |
Формулы перехода от одного основания логарифма к другому.
![]() (
(![]() )
)
Примеры выполнения заданий.
Задание. Вычислить ![]() , если
, если ![]()
Решение. Перепишем данное выражение, используя свойство логарифма степени и логарифма произведения:
![]()
Ответ. ![]()
Пример.
82log83 = (82log83)2 = 32 = 9
Логарифм произведения равен сумме логарифмов
loga (bc) = logab + logac
Пример.
log38,1 + log310 = log3 (8,1*10) = log381 = 4
Логарифм частного равен разности логарифмов
loga (b/c) = logab - logac
Пример.
9 log550/9 log52 = 9 log550- log52 = 9 log525 = 9 2 = 81
Свойства степени логарифмируемого числа и основания логарифма
Показатель степени логарифмируемого числа logab m = mlogab
Показатель степени основания логарифма loganb =1/n*logab
loganb m = m/n*logab,
если m = n, получим loganb n = logab
Пример.
log49 = log223 2 = log23
Переход к новому основанию
logab = logcb/logca,
если c = b, получим logbb = 1
тогда logab = 1/logba
Пример.
log0,83*log31,25 = log0,83*log0,81,25/log0,83 = log0,81,25 = log4/55/4 = -1
Самостоятельное выполнение задания.
Задания.
Вариант 1.
Вычислите. ![]()
Найдите значение выражения ![]()
Вычислите ![]()
Выполните действие ![]()
Сократите дробь ![]()
Вычислите ![]()
Найдите ![]() , если
, если ![]()
Найдите число а по его логарифму :![]()
Вариант 2.
Вычислите ![]()
Найдите значение выражения ![]()
Вычислите ![]()
Выполните действие ![]()
Сократите дробь ![]()
Вычислите ![]()
Известно, что ![]() . Найдите
. Найдите ![]()
Найдите число b по его логарифму ![]()
Вариант 3.
Вычислите ![]()
Найдите значение выражения ![]()
Выполните действие ![]()
Сократите дробь ![]()
Вычислите ![]()
Вычислите ![]()
Известно, что ![]() . Найдите
. Найдите ![]()
Найдите число k по его логарифму ![]()
Вариант 4.
Вычислите ![]()
Найдите значение выражения ![]()
Вычислите ![]()
Выполните действие ![]()
Сократите дробь ![]()
Вычислите ![]()
Известно, что ![]() . Найдите
. Найдите ![]()
Найдите число х по его логарифму :![]()
Вариант 5
1.Вычислите ![]()
2. Найдите значение выражения ![]()
3. Вычислите ![]()
4. Выполните действие ![]()
5. Вычислите ![]()
6. Известно, что ![]() . Найдите
. Найдите ![]()
7. Найдите значение выражения ![]()
8. Найдите число x , если ![]()
Вариант 6
Вычислите ![]()
Найдите значение выражения ![]()
Вычислите ![]()
Найдите значение выражения ![]()
Вычислите ![]()
Известно, что ![]() . Найдите
. Найдите ![]()
Сократите дробь ![]()
Найдите число k по его логарифму ![]()
Сделать вывод
ПРАКТИЧЕСКАЯ РАБОТА №4
по учебной дисциплине «Математика»
Тема: Преобразование выражений.
Цель: Научиться преобразовывать выражения, содержащие степени, корни, применять тождества сокращенного умножения.
Оборудование: 1) методическое пособие по выполнению работы
2) Учебник Математика ДадаянА.А.
3) Учебник Математика Башмаков М.И.
Время выполнения: Повторение теоретического материала – 12 минут, решение по образцу – 18 минут, самостоятельное выполнение заданий – 60 минут.
Ход работы:
Повторение теоретического материала.
Преобразование алгебраических выражений: первый этап их изучения — числа, переменные, степени («цифры»); второй этап их изучения — одночлены («натуральные числа»); третий этап их изучения — многочлены («целые числа»); четвертый этап их изучения — алгебраические дроби
(«рациональные числа»). При этом каждый следующий этап как бы вбирает в себя предыдущий: так, числа, переменные, степени — частные случаи одночленов; одночлены — частные •случаи многочленов; многочлены — частные случаи алгебраических дробей. Между прочим, в алгебре используют иногда и такие термины: многочлен — целое выражение, алгебраическая дробь — дробное выражение (это лишь усиливает аналогию).
Вы знаете, что любое числовое выражение после выполнения всех входящих в его состав арифметических действий принимает конкретное числовое значение — рациональное число (разумеется, оно может оказаться и натуральным числом, и целым числом, и дробью — это неважно). Точно так же любое алгебраическое выражение, составленное из чисел и переменных с помощью арифметических операций и возведения в натуральную степень, после выполнения преобразований принимает вид алгебраической дроби и опять-таки, в частности, может получиться не дробь, а многочлен или даже одночлен). Для таких выражений в алгебре используют термин рациональное выражение.
Пример. Доказать тождество
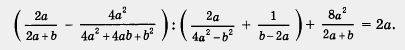
Решение.
Доказать тождество — это значит установить, что при всех допустимых значениях переменных его левая и правая части представляют собой тождественно равные выражения. В алгебре тождества доказывают различными способами:
1) выполняют преобразования левой части и получают в итоге правую часть;
2) выполняют преобразования правой части и получают в итоге левую часть;
3) по отдельности преобразуют правую и левую части и получают и в первом и во втором случае одно и то же выражение;
4) составляют разность левой и правой частей и в результате ее преобразований получают нуль.
Какой способ выбрать — зависит от конкретного вида тождества, которое вам предлагается доказать. В данном примере целесообразно выбрать первый способ.
Для преобразования рациональных выражений принят тот же порядок действий, что и для преобразования числовых выражений. Это значит, что сначала выполняют действия в скобках, затем действия второй ступени (умножение, деление, возведение в степень), затем действия первой ступени (сложение, вычитание).
Выполним преобразования по действиям:

Как видите, нам удалось преобразовать левую часть проверяемого тождества к виду правой части. Это значит, что тождество доказано. Однако напомним, что тождество справедливо лишь для допустимых значений переменных. Таковыми в данном примере являются любые значения а и b, кроме тех, которые обращают знаменатели дробей в нуль. Значит, допустимыми являются любые пары чисел (а; b), кроме тех, при которых выполняется хотя бы одно из равенств:
2а - b = 0, 2а + b = 0, b = 0.
Преобразование степенных выражений:
Применение определения и свойств степени с натуральным показателем.
Применение определения и свойств степени с целым показателем.
Применение определения и свойств степени с рациональным показателем.
Применение определения и свойств степени с действительным показателем.
II. Преобразования иррациональных выражений:
Применение определения и свойств арифметического квадратного корня.
Применение определения и свойств корня n – ой степени.
Вынесение множителя из-под знака корня и внесение множителя под знак корня.
Сокращение дробей.
Освобождение от иррациональности.
Применение формул сокращенного умножения для упрощения иррациональных выражений.
III. Преобразование тригонометрических выражений:
Применение определений понятий синус, косинус, тангенс, котангенс произвольного угла.
Применение определения понятия радианная мера угла.
Применение основных тригонометрических тождеств.
Применение формул привидения.
Применение формул синус, косинус, тангенс суммы двух произвольных углов.
Применение формул синус, косинус, тангенс суммы двойного угла.
IV. Преобразование логарифмических выражений:
Применение определения понятия логарифм числа.
Применение свойств логарифмов (произведения, частного, степени).
Применение определения десятичного логарифма, натурального логарифма, числа е.
Рассмотрим несколько примеров.
Пример 1. Упростить выражение: √(16*a^4/4b^6);
Решение: √(16*a^4/4b^6) =√(16*a^4)/ √(4b^6) = 4*a^2/2*b^3.
Ответ: √(16*a^4/4b^6) = 4*a^2/2*b^3;
Пример 2. Вынести множитель из-под знака квадратного корня: √(9*a^7*b^3);
Решение: √(9*a^7*b^3) = √(9*a^6*a*b^2*b)= √9*√a^6*√a*√b^2*√b = 3*a^3*b*√(a*b);
Ответ: √(9*a^7*b^3) = 3*a^3*b*√(a*b);
Пример 3. Внести множитель под знак квадратного корня: (3*a*√b)/( √ (3*a));
Решение: (3*a*√b)/ √(3*a) = ((√(9*a^2) )*(√b))/ √(3*a) = √((9*a^2*b)/3*a)= √(3*a*b);
Ответ: (3*a*√b)/ √(3*a) = √(3*a*b);
Пример 1. ![]() . Данное выражение имеет смысл при
. Данное выражение имеет смысл при ![]() . Учитывая свойства корней, вынесем множители из – под знака корня. Получим:
. Учитывая свойства корней, вынесем множители из – под знака корня. Получим:
![]() =
= ![]() =
= ![]() =
=![]() =
=![]() =
=![]() .
.
Пример 2. Упростим выражение ![]() .
.
Выполним упрощение с помощью формулы сокращенного умножения. Получим: ![]()
![]() =
= ![]() = 4-х. ( при условии х
= 4-х. ( при условии х![]() .
.
Пример 3. Преобразуем выражение: ![]() .
.
Умножим каждый член первого выражения на каждый член второго выражения подобно произведению многочленов. Получим:
![]() =
= ![]() =
= ![]() = 108-8 = 100.
= 108-8 = 100.
С другой стороны, есть второй способ решения. Из первой скобки вынести общий множитель 4. Получим ![]() . Далее применим формулу разность квадратов:
. Далее применим формулу разность квадратов: ![]() = 4(27-2) = 100.
= 4(27-2) = 100.
Пример 4. Сократите дробь ![]() .
.
Представим ![]() , 5 =
, 5 = ![]() . Тогда числитель дроби можно разложить на множители, используя формулу разности квадратов. Получаем:
. Тогда числитель дроби можно разложить на множители, используя формулу разности квадратов. Получаем:
![]() =
= ![]() =
= ![]() .
.
Пример 5. Сократите дробь ![]() .
.
Разложим на множители числитель дроби, используя формулу разности квадратов, и знаменатель дроби, используя формулу квадрата разности. Получаем:
![]() .
.
3. Самостоятельное выполнение заданий
Вариант 1
Вычислить: ![]()
Найдите значение выражения ![]() при
при ![]() .
.
Найдите значение выражения ![]() при
при ![]() .
.
Упростить: ![]()
Вычислите: (2log27)log725
Найдите значение выражения
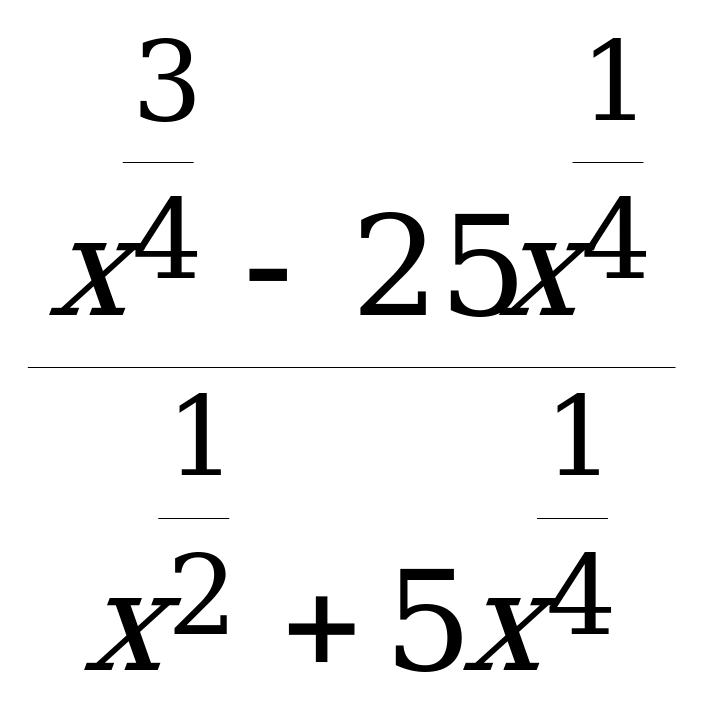 при x=81.
при x=81.
------------------------------------------------------------------------------------
Вариант 2
Вычислить: ![]()
Найдите значение выражения ![]() при
при ![]() .
.
Найдите значение выражения ![]() при
при ![]() .
.
Упростить:![]()
Вычислить log464-log5(1/5)+log13![]() ,
,
Найдите значение выражения
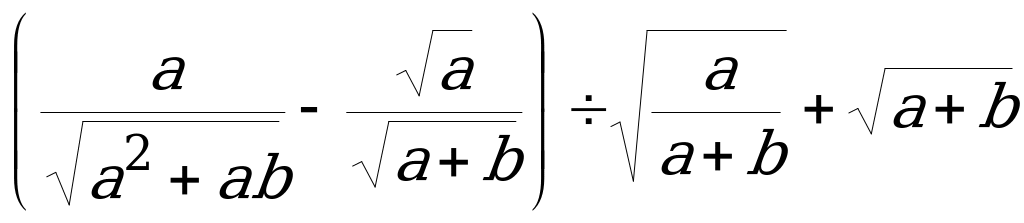 при
при ![]() =4,
=4, ![]() =5.
=5.
---------------------------------------------------------------------
Вариант 3.
Вычислить: ![]()
Найдите значение выражения ![]() при
при ![]() .
.
Найдите значение выражения ![]() при
при ![]() .
.
Упростить:![]()
Вычислить log2 32-log3(1/27)-log32![]() ,
,
Найдите значение выражения:
![]()
при а = 17 и b = 51
Вариант 4
Вычислить: ![]()
Найдите значение выражения ![]() при
при ![]() .
.
Найдите значение выражения ![]() при
при ![]() .
.
Упростить:![]()
Вычислить log5125+log4(1/64)-log17![]() ,
,
Найти значение выражения
![]()
при х = 144 и y = 27
-----------------------------------------------------------------------------
Вариант 5
Вычислить: ![]()
Найдите значение выражения ![]() при
при ![]() .
.
Найдите значение выражения ![]() при
при ![]() .
.
Упростить:![]()
Вычислить log 7 49-log 1/6(36)+log131![]() ,
,
Найдите значение выражения
![]()
при а = 25 и b = 35
-------------------------------------------------------------------------
Вариант 6
Вычислить: ![]()
Найдите значение выражения  при
при ![]() .
.
Найдите значение выражения ![]() при
при ![]() .
.
Упростить:![]()
Вычислить log564:log54
Найдите значение выражения
 , если x=4 , y=25.
, если x=4 , y=25.
4. Сделайте вывод.
ПРАКТИЧЕСКАЯ РАБОТА №5
по учебной дисциплине «Математика»
Тема: Основные тригонометрические тождества.
Цель: Научиться применять тригонометрические тождества для преобразования выражений.
Оборудование: 1) Методическое пособие по выполнению работы
2) Учебник Математика ДадаянА.А.
3)Учебник Математика Башмаков М.И.
Время выполнения: Повторение теоретического материала – 12 минут, решение по образцу – 18 минут, самостоятельное выполнение заданий – 60 минут.
Ход работы:
Повторение теоретического материала.
Основные тригонометрические тождества
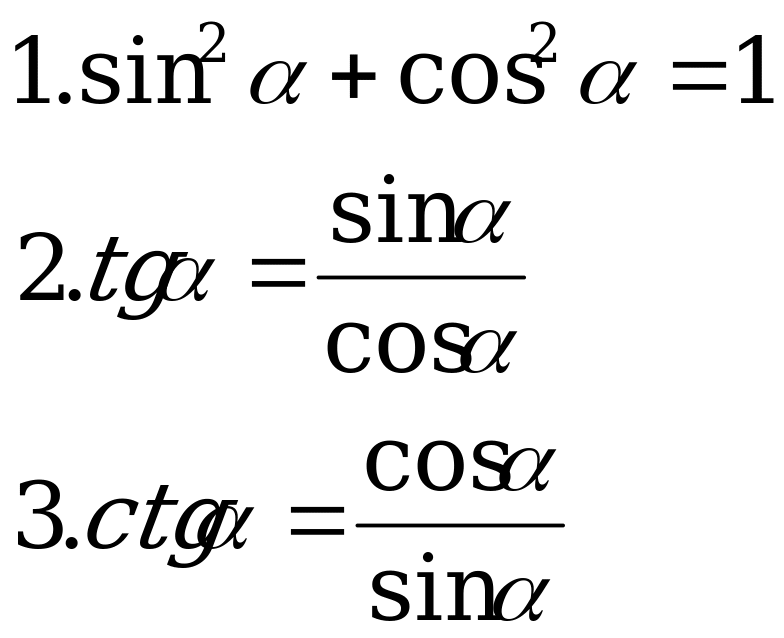
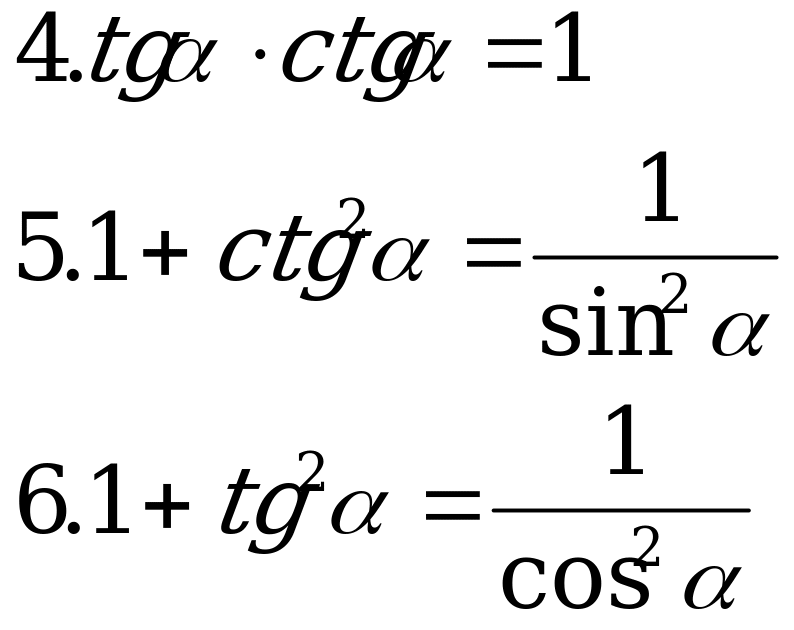
Синус, косинус, тангенс суммы и разности

Синус, косинус, тангенс двойного угла.
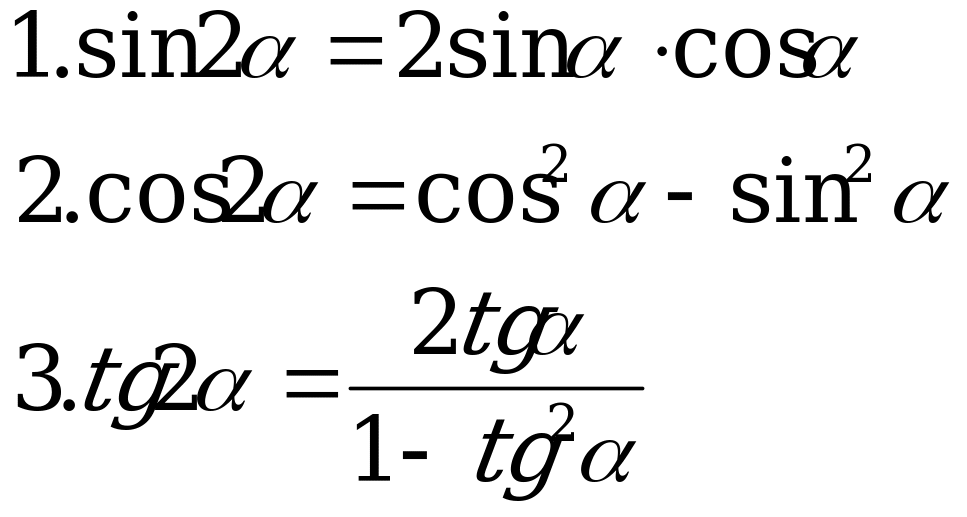
2. Примеры выполнения заданий
Задача
Найдите sin α, если известно следующее:
![]()
Решение
Нам известен косинус, но неизвестен синус. Основное тригонометрическое тождество (в «чистом» виде) связывает как раз эти функции, поэтому будем работать с ним. Имеем:
sin2 α + cos2 α = 1 ⇒ sin2 α + 99/100 = 1 ⇒ sin2 α = 1/100 ⇒ sin α = ±1/10 = ±0,1.
Для решения задачи осталось найти знак синуса. Поскольку угол α ∈ (π/2; π), то в градусной мере это записывается так: α ∈ (90°; 180°).
Следовательно, угол α лежит во II координатной четверти — все синусы там положительны. Поэтому sin α = 0,1.
Ответ: 0,1
Задача
Найдите cos α, если известно следующее:
![]()
Решение
Итак, нам известен синус, а надо найти косинус. Обе эти функции есть в основном тригонометрическом тождестве. Подставляем:
sin2 α + cos2 α = 1 ⇒ 3/4 + cos2 α = 1 ⇒ cos2 α = 1/4 ⇒ cos α = ±1/2 = ±0,5.
Осталось разобраться со знаком перед дробью. Что выбрать: плюс или минус? По условию, угол α принадлежит промежутку (π 3π/2). Переведем углы из радианной меры в градусную — получим: α ∈ (180°; 270°).
Очевидно, это III координатная четверть, где все косинусы отрицательны. Поэтому cos α = −0,5.
Ответ: −0,5
Задача
Найдите tg α, если известно следующее:
![]()
Решение
Тангенс и косинус связаны уравнением, следующим из основного тригонометрического тождества:
![]()
Получаем: tg α = ±3. Знак тангенса определяем по углу α. Известно, что α ∈ (3π/2; 2π). Переведем углы из радианной меры в градусную — получим α ∈ (270°; 360°).
Очевидно, это IV координатная четверть, где все тангенсы отрицательны. Поэтому tg α = −3.
Ответ: −3
Задача
Найдите cos α, если известно следующее:
![]()
Решение
Снова известен синус и неизвестен косинус. Запишем основное тригонометрическое тождество:
sin2 α + cos2 α = 1 ⇒ 0,64 + cos2 α = 1 ⇒ cos2 α = 0,36 ⇒ cos α = ±0,6.
Знак определяем по углу. Имеем: α ∈ (3π/2; 2π). Переведем углы из градусной меры в радианную: α ∈ (270°; 360°) — это IV координатная четверть, косинусы там положительны. Следовательно, cos α = 0,6.
Ответ: 0,6
Задача
Найдите sin α, если известно следующее:
![]()
Решение
Запишем формулу, которая следует из основного тригонометрического тождества и напрямую связывает синус и котангенс:
![]()
Отсюда получаем, что sin2 α = 1/25, т.е. sin α = ±1/5 = ±0,2. Известно, что угол α ∈ (0; π/2). В градусной мере это записывается так: α ∈ (0°; 90°) — I координатная четверть.
Итак, угол находится в I координатной четверти — все тригонометрические функции там положительны, поэтому sin α = 0,2.
Ответ: 0,2
3. Самостоятельное выполнение задания.
Вариант №1
1.Определите знак выражения: cos 7000 tg 3800, cos 3180 ∙ tg (−2140).
2.Найдите cos 2a, tg a, если известно, что sin a=1/5, π/2≤a≤ π.
3.Упростите выражение ![]()
4.Вычислить ![]()
5. Докажите тождество sin4a + 2sin2a cos2a + cos4a + sin2a + cos2a = 2.
Вариант №2
Определите знак выражения: sin 2000 ctg 3400, cos 2850 ∙ cos (−3160)
Найдите ctg a , sin 2a, , если известно, что cos a=![]() , 3 π /2≤a≤2 π.
, 3 π /2≤a≤2 π.
Упростите выражение ![]()
Вычислить ![]()
Докажите тождество ![]() (sin4a - 2sin2a cos2a + cos4a) : (sin a + cos a)2 = 1 - sin2a.
(sin4a - 2sin2a cos2a + cos4a) : (sin a + cos a)2 = 1 - sin2a.
Вариант №3
Определите знак выражения: cos 5000 ctg 8000, sin 3 ∙ cos 4 ∙ tg 5
Найдите cos 2a, tg a, , если известно, что sin a = - 0,8 , 1800≤a≤2700.
Упростите выражение ![]()
Вычислить ![]()
5.Докажите тождество ![]() (sin4a + sin2a cos2a) : cos2 a = 1/ cos2 a - 1.
(sin4a + sin2a cos2a) : cos2 a = 1/ cos2 a - 1.
Вариант №4
Найдите sin 2a, tg a, , если известно, что cos a= - 24/25, 900≤a≤1800.
Определите знак выражения: sin 4600 tg 6000, cos 2850 ∙ cos (−3160)
Упростите ![]()
Вычислите ![]()
Докажите тождество ![]()
Вариант №5
Найдите ctg a , cos 2a, если известно, что cos a= - ![]() , π /2 ≤a≤ π.
, π /2 ≤a≤ π.
Упростите ![]()
Определите знак выражения: tg 2500 ctg 1000, sin 1000 ∙ sin 1320
Вычислить ![]()
Докажите тождество ![]()
Вариант №6
Найдите sin a , sin 2a, ctg a, если известно, что tg a= - 3, 3 π /2≤a≤2 π.
Упростите ![]()
Определите знак выражения: cos 7000 tg 9600, sin (−2800) sin (−3)
Вычислить ![]()
Докажите тождество ![]() (tg a – sin a)(cos2 a/sina + ctg a) = sin2 a.
(tg a – sin a)(cos2 a/sina + ctg a) = sin2 a.
4. Сделайте вывод
ПРАКТИЧЕСКАЯ РАБОТА №6
по учебной дисциплине «Математика»
Тема: Решение тригонометрических уравнений.
Цель: Научиться решать тригонометрические уравнения.
Оборудование: 1 )Методическое пособие по выполнению работы
2) Учебник Математика ДадаянА.А.
3)Учебник Математика Башмаков М.И.
Время выполнения: Повторение теоретического материала – 12 минут, решение по образцу – 18 минут, самостоятельное выполнение заданий – 60 минут.
Ход работы:
Повторение теоретического материала.
Значения тригонометрических функций некоторых углов.
| x | 0 |
|
|
| 1 | -1 |
| arcsin x | 0 |
|
|
|
| - |
| arсcos x |
|
|
|
| 0 |
|
| x | 0 |
| 1 |
|
| arctg x | 0 |
|
|
|
| arcctg x |
|
|
|
|
Формулы для решения простейших тригонометрических уравнений.
sin x = a ; | a | ![]() ; x=(-1)n arcsin a +
; x=(-1)n arcsin a +![]() n, n
n, n![]() Z;
Z;
sin x =0; x=![]() k, k
k, k![]() Z;
Z;
sin x = 1; x= ![]() +2
+2![]() k; k
k; k![]() Z;
Z;
sin x = -1 ; x= - ![]() + 2
+ 2![]() k; k
k; k![]() Z;
Z;
cos x = a ; |a| ![]() ; x=
; x= ![]() arcos a +2
arcos a +2![]() n, n
n, n![]() Z;
Z;
cos x = 0; x = ![]() +
+![]() k; k
k; k![]() Z;
Z;
cos x = 1 ; x = 2![]() k; k
k; k![]() Z;
Z;
cos x = -1 ; x = ![]() +2
+2![]() k; k
k; k![]() Z;
Z;
tg x = a ; x = arctg a + ![]() n; n
n; n![]() Z;
Z;
ctg x = a; x = arcctg a +![]() n; n
n; n ![]() Z.
Z.
2. Примеры выполнения заданий .
1) Решить уравнение 2 cos 2 x +sin x + 1 =0
Как представим cos 2 x?
Какое уравнение получается?
2(1- sin 2 x) + sin x + 1=0
2- 2 sin 2 x +sin x + 1 =0 Приведём подобные.
- 2 sin 2 x + sin x + 3 = 0 | -1 Умножим на –1.
2 sin 2 x – sin x – 3 =0
sin x = y
2 y 2 – y – 3 = 0
D=1+24=250 = два корня.
y 1 = (1+5)/4 = 6/4 = 3/2;
y 2 = (1-5)/4= - 1.
Мы получили два уравнения:
sin x =3/2 ; sin x =1;
E (sin x )=[-1;1 ] x =(-1)karcsin(-1) +Пk, k Z;
Корней нет; x =(-1)k * (- П/2 ) + Пk, k Z;
или
x =(-1)k * 3П/2 + Пk, k ![]() Z;
Z;
Ответ: x =(-1)k * 3П/2 + Пk, k ![]() Z;
Z;
2) Решить уравнение 6 cos 2 x + cos x – 1 = 0
cos x = y;
6y 2 + y – 1 = 0;
D = 1+24=250, два корня.
y 1= (- 1+5)/12=1/3; y 2 = (-1+5)/12=-6/12= - 1/2
cos x = 1/3; cos x = - 1/ 2
x1 = ± arccos 1/3 + 2 Пk;k ![]() Z; x 2 = ± arccos(-1/2) +2 Пk; k
Z; x 2 = ± arccos(-1/2) +2 Пk; k ![]() Z;
Z;
x 2 = ± 2П/3 + 2Пk, k ![]() Z;
Z;
Ответ: x1 = ± arccos 1/3 + 2 Пk; k ![]() Z; x2 = ± 2П/3 + 2Пk, k
Z; x2 = ± 2П/3 + 2Пk, k![]() Z;
Z;
2. Самостоятельное выполнение задания.
Вариант 1
Вычислите: arcsin (-![]() ) + 2arcctg (-
) + 2arcctg (-![]() ) – arctg 1.
) – arctg 1.
Решите уравнения:
1) sinх =![]() , 2) cosх =
, 2) cosх =![]() , 3) tgх=
, 3) tgх=![]() , 4) ctgх=1,
, 4) ctgх=1,
5) sinх = -![]() , 6) cosх = -1, 7) tgх=-
, 6) cosх = -1, 7) tgх=-![]() , 8) ctgх=-
, 8) ctgх=-![]() .
.
3.* Решить уравнения: 1) sin 4x = ![]() , 2) tg (x-
, 2) tg (x-![]() ) =
) =![]() , 3) ctgx (2-cosx)=0.
, 3) ctgx (2-cosx)=0.
4) cos2x – sin2 x = - ![]() , 5) sin 3x cos(x+
, 5) sin 3x cos(x+![]() ) + cos 3x sin(x+
) + cos 3x sin(x+![]() ) = 0.
) = 0.
6) 2 sin2 x - 5 sin x – 3 = 0, 7) tg x + 2ctgx = 3.
Вариант 2
1. Вычислите: arccos (-![]() ) - 3arctg (-
) - 3arctg (-![]() ) + 4 arcctg 1.
) + 4 arcctg 1.
2. Решите уравнения:
1) sinх=![]() , 2) cosх=0, 3) tgх=1, 4) ctgх=
, 2) cosх=0, 3) tgх=1, 4) ctgх=![]() ,
,
5) sinх=-![]() , 6) cosх=-
, 6) cosх=-![]() , 7) tgх=-
, 7) tgх=-![]() , 8) ctgх=-1.
, 8) ctgх=-1.
3.* Решить уравнения: 1) сos 3x = ![]() , 2) ctg (x+
, 2) ctg (x+![]() ) = -
) = -![]() , 3) tgx (3-sinx)=0.
, 3) tgx (3-sinx)=0.
4) 2cosx sin x = ![]() , 5) cos 2x cos(x+
, 5) cos 2x cos(x+![]() ) + sin 2x sin(x+
) + sin 2x sin(x+![]() ) = 0.
) = 0.
6) 2 сos2 x - cos x – 1 = 0, 7) ctg x + tgx = 2 .
Вариант 3
Вычислите: 2arcsin ![]() + arcctg (-
+ arcctg (-![]() ) – 2arccos (- 1).
) – 2arccos (- 1).
Решите уравнения:
1) sinх=![]() , 2) cosх=
, 2) cosх=![]() , 3) tgх=
, 3) tgх=![]() , 4) ctgх=
, 4) ctgх=![]() ,
,
5) sinх=-1, 6) cosх=-![]() , 7) tgх=-1, 8) ctgх=0.
, 7) tgх=-1, 8) ctgх=0.
3.* Решить уравнения: 1) tg 5x =-![]() , 2) sin (x+
, 2) sin (x+![]() ) =
) =![]() , 3) cosx (6-ctgx)=0.
, 3) cosx (6-ctgx)=0.
4) sin2 x - cos2x =![]() , 5) sin 2x cos(x-
, 5) sin 2x cos(x-![]() ) - cos 2x sin(x-
) - cos 2x sin(x-![]() ) = 0.
) = 0.
6) 2 sin2 x - 5 sin x +2 = 0, 7) 2tg x + 2ctgx = 5 .
Вариант 4
1. Вычислите: 3arctg (-1) - 5arcctg (-![]() ) + arccos 1.
) + arccos 1.
2. Решите уравнения:
1) sinх=1, 2) cosх=![]() , 3) tgх=
, 3) tgх=![]() , 4) ctgх=1,
, 4) ctgх=1,
5) sinх=-![]() , 6) cosх=-
, 6) cosх=-![]() , 7) tgх=0, 8) ctgх=-
, 7) tgх=0, 8) ctgх=-![]() .
.
3.* Решить уравнения: 1) ctg 3x = -1, 2) 2cos (x+![]() ) =1, 3) sinx (2+tgx)=0.
) =1, 3) sinx (2+tgx)=0.
4) sin x cos x =1, 5) cos 4x cos(x+![]() ) + sin 4x sin(x+
) + sin 4x sin(x+![]() ) = 0.
) = 0.
6) sin2 x - 4 sin x + 3 = 0, 7) 3tg x - 3ctgx = 8.
Вариант 5
1. Вычислите: 5arcsin (-![]() ) + 2arcctg (-1) – arctg 1.
) + 2arcctg (-1) – arctg 1.
2. Решите уравнения:
1) sinх=0, 2) cosх=![]() , 3) tgх=1, 4) ctgх=0,
, 3) tgх=1, 4) ctgх=0,
5) sinх=-![]() , 6) cosх=-
, 6) cosх=-![]() , 7) tgх=-
, 7) tgх=-![]() , 8) ctgх=-
, 8) ctgх=-![]() .
.
3.* Решить уравнения: 1) sin 7x = -![]() , 2) ctg (x-
, 2) ctg (x-![]() ) =2, 3) tgx (1-2cosx)=0.
) =2, 3) tgx (1-2cosx)=0.
4) 2cos2x – 2sin2 x =1, 5) sin 4x cos(x-![]() ) + cos 4x sin(x-
) + cos 4x sin(x-![]() ) = 0.
) = 0.
6) 4 sin2 x - sin x – 3 = 0, 7) 4tg x + 3ctgx = 7 .
Вариант 6
1. Вычислите: arсcos![]() - 2arcctg (-
- 2arcctg (-![]() ) +3 arcsin(- 1).
) +3 arcsin(- 1).
2. Решите уравнения:
1) sinх=![]() , 2) cosх=1, 3) tgх=
, 2) cosх=1, 3) tgх=![]() , 4) ctgх=-1,
, 4) ctgх=-1,
5) sinх=-![]() , 6) cosх=0, 7) tgх=-
, 6) cosх=0, 7) tgх=-![]() , 8) ctgх=0.
, 8) ctgх=0.
3.* . Решить уравнения: 1) cos 2x = - ![]() , 2) ctg (
, 2) ctg (![]() - x) =
- x) =![]() ,
,
3) tgx (1-2sinx)=0, 4) cos2x –![]() = sin2 x,
= sin2 x,
5) sin 2x sin(x+![]() ) - cos 2x cos(x+
) - cos 2x cos(x+![]() ) = 0.
) = 0.
6) sin2 x - 5 sin x +4 = 0, 7) tg x + 2ctgx = 3 .
ПРАКТИЧЕСКАЯ РАБОТА №7
по учебной дисциплине «Математика»
Тема: Решение тригонометрических неравенств.
Цель: Научиться решать тригонометрические неравенства.
Оборудование: 1) Методическое пособие по выполнению работы
2) Учебник Математика ДадаянА.А.
3) Учебник Математика Башмаков М.И.
Время выполнения: Повторение теоретического материала – 12 минут, решение по образцу – 18 минут, самостоятельное выполнение заданий – 60 минут.
Ход работы:
Повторение теоретического материала.
Значения тригонометрических функций некоторых углов.
| x | 0 |
|
|
| 1 | -1 |
| arcsin x | 0 |
|
|
|
| - |
| arcos x |
|
|
|
| 0 |
|
| x | 0 |
| 1 |
|
| arctg x | 0 |
|
|
|
| arcctg x |
|
|
|
|
Формулы для решения простейших тригонометрических неравенств.
sin x (arcsin a+2![]() n; 3
n; 3![]() - arcsin a+2
- arcsin a+2![]() n), n
n), n![]() Z
Z
sin x a; x ![]() ( arcsin a+2
( arcsin a+2![]() n;
n; ![]() - arcsin a+2
- arcsin a+2![]() n), n
n), n![]() Z
Z
cos x ( arccos a+2![]() n; 2
n; 2![]() - arcsin a+2
- arcsin a+2![]() n), n
n), n![]() Z
Z
cos x a; x ![]() ( -arccos a+2
( -arccos a+2![]() n; arcsin a+2
n; arcsin a+2![]() n), n
n), n![]() Z
Z
tg x (-![]() ; arctg a +
; arctg a + ![]() n); n
n); n![]() Z;
Z;
tgxa; x![]() (arctg a +
(arctg a + ![]() n;
n;![]() ; ); n
; ); n![]() Z;
Z;
ctg x ( arcctg a +![]() n;
n; ![]() +
+![]() n);n
n);n ![]() Z.
Z.
ctg xa ; x![]() (
( ![]() n ;arcctg a +
n ;arcctg a +![]() n);n
n);n ![]() Z.
Z.
Примеры выполнения заданий .
Решить неравенство sin x![]()
![]()

![]()







![]()
![]()
Ответ : x![]()


2)Решить неравенство cos x![]()






![]()
![]()
![]()
Ответ: x![]()
Самостоятельное выполнение задания.
Вариант 1.
1.Решите неравенства:
1) sinх≤1, 2) cosх≥![]() , 3) tgх≤
, 3) tgх≤![]() , 4) ctgх≥1,
, 4) ctgх≥1,
5) sinх≥![]() , 6) cosх
, 6) cosх![]() , 7) tgх 0, 8) ctgх≤
, 7) tgх 0, 8) ctgх≤![]() .
.
Определите знак выражения: cos 7000 tg 3800.
Найдите cos a , если известно, что sin a=1/5, π/2≤a≤ π.
Решите неравенства:
1) sin2х ≥![]() , 2) cos(х+
, 2) cos(х+![]() )
)![]() , 3) tg
, 3) tg![]() х
х![]() , 4) ctg4х1,
, 4) ctg4х1,
5) sin(![]() -х )≤
-х )≤ ![]() , 6) cos(-3х)≥ 1, 7) tg3х≥
, 6) cos(-3х)≥ 1, 7) tg3х≥![]() , 8) ctg
, 8) ctg![]() х≤
х≤![]() .
.
Вариант 2.
1. Решите неравенства:
1) sinх≥0, 2) cosх![]() , 3) tgхctgх0,
, 3) tgхctgх0,
5) sinх≤![]() , 6) cosх≥
, 6) cosх≥![]() , 7) tgх≥
, 7) tgх≥![]() , 8) ctgх≤
, 8) ctgх≤![]() .
.
Определите знак выражения: sin 2000 ctg 3400.
Найдите tg a , если известно, что cos a=![]() , 3 π /2≤a≤2 π.
, 3 π /2≤a≤2 π.
4. Решите неравенства:
1) sin3х≤![]() , 2) cos(-х)≥1, 3) tg
, 2) cos(-х)≥1, 3) tg![]() х , 4) ctg5х≤1,
х , 4) ctg5х≤1,
5) sin(![]() -х)≥
-х)≥![]() , 6) cos
, 6) cos![]() хtg2х≥
хtg2х≥![]() , 8) ctg7х0.
, 8) ctg7х0.
Вариант 3.
1. Решите неравенства:
1) sinх≤![]() , 2) cosх≥1, 3) tgх , 4) ctgх≤-1,
, 2) cosх≥1, 3) tgх , 4) ctgх≤-1,
5) sinх≥-![]() , 6) cosхtgх≥-
, 6) cosхtgх≥-![]() , 8) ctgх0.
, 8) ctgх0.
Определите знак выражения: cos 5000 ctg 8000.
Найдите ctg a , если известно, что sin a = - 0,8 , 1800≤a≤2700.
Решите неравенства:
1) sin(х+![]() )≤
)≤![]() , 2) cos2х≥
, 2) cos2х≥![]() , 3) tg(-3х) , 4) ctg2х
, 3) tg(-3х) , 4) ctg2х![]() ,
,
5) sin![]() х≥1, 6) cos(
х≥1, 6) cos(![]() -х)
-х)![]() , 7) tgх≥-1, 8) ctgх≤0.
, 7) tgх≥-1, 8) ctgх≤0.
Вариант 4.
1. Решите неравенства:
1) sinх ≥![]() , 2) cosх
, 2) cosх ![]() , 3) tgх
, 3) tgх![]() , 4) ctgх1,
, 4) ctgх1,
5) sinх ≤ -![]() , 6) cosх≥ -1, 7) tgх≥-
, 6) cosх≥ -1, 7) tgх≥-![]() , 8) ctgх≤-
, 8) ctgх≤-![]() .
.
Найдите tg a , если известно, что cos a= - 24/25, 900≤a≤1800.
Определите знак выражения: sin 4600 tg 6000.
Решите неравенства:
1) sin2х ≥![]() , 2) cos(х+
, 2) cos(х+![]() )
)![]() , 3) tg
, 3) tg![]() х
х![]() , 4) ctg4х1,
, 4) ctg4х1,
5) sin(![]() -х )≤
-х )≤ ![]() , 6) cos(-3х)≥ 1, 7) tg3х≥
, 6) cos(-3х)≥ 1, 7) tg3х≥![]() , 8) ctg
, 8) ctg![]() х≤
х≤![]() .
.
Вариант 5.
1. Решите неравенства:
1) sinх≥![]() , 2) cosхtgх≤1, 4) ctgх≥
, 2) cosхtgх≤1, 4) ctgх≥![]() ,
,
5) sinх≤-![]() , 6) cosх≥-
, 6) cosх≥-![]() , 7) tgх -
, 7) tgх -![]() , 8) ctgх≤-1.
, 8) ctgх≤-1.
Найдите tg a , если известно, что cos a= - ![]() , π /2 ≤a≤ π.
, π /2 ≤a≤ π.
Определите знак выражения: tg 2500 ctg 1000.
4. Решите неравенства:
1) sin3х≤![]() , 2) cos(-х)≥1, 3) tg
, 2) cos(-х)≥1, 3) tg![]() х , 4) ctg5х≤1,
х , 4) ctg5х≤1,
5) sin(![]() -х)≥
-х)≥![]() , 6) cos
, 6) cos![]() хtg2х≥
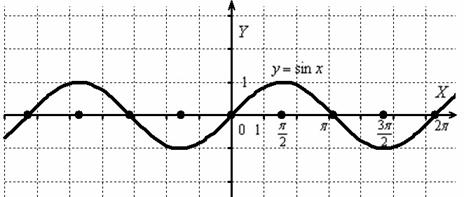
хtg2х≥![]() , 8) ctg7х0.
, 8) ctg7х0.
Вариант 6.
1. Решите неравенства:
1) sinх≤![]() , 2) cosх≥
, 2) cosх≥![]() , 3) tgх , 4) ctgх
, 3) tgх , 4) ctgх![]() ,
,
5) sinх≥-1, 6) cosх![]() , 7) tgх≥-1, 8) ctgх≤0.
, 7) tgх≥-1, 8) ctgх≤0.
Найдите sin a , если известно, что tg a= - 3, 3 π /2≤a≤2 π.
Определите знак выражения: cos 7000 tg 9600.
Решите неравенства:
1) sin(х+![]() )≤
)≤![]() , 2) cos2х≥
, 2) cos2х≥![]() , 3) tg(-3х) , 4) ctg2х
, 3) tg(-3х) , 4) ctg2х![]() ,
,
5) sin![]() х≥1, 6) cos(
х≥1, 6) cos(![]() -х)
-х)![]() , 7) tgх≥-1, 8) ctgх≤0.
, 7) tgх≥-1, 8) ctgх≤0.
ПРАКТИЧЕСКАЯ РАБОТА №8
по учебной дисциплине «Математика»
Тема: Исследование функций и построение графиков.
Цель: Научиться исследовать функции и строить их графики.
Оборудование: 1) Методическое пособие по выполнению работы
2) Учебник Математика ДадаянА.А.
3)Учебник Математика Башмаков М.И.
Время выполнения: Повторение теоретического материала – 12 минут, решение по образцу – 18 минут, самостоятельное выполнение заданий – 60 минут.
Ход работы:
Повторение теоретического материала.
Схема исследования функции и построение её графика.
Найти область определения функции.
Найти область значений функции. Обычно этот пункт пропускают или заполняют после исследования на экстремумы.
Исследовать непрерывность функции, выделить особые точки (точки разрыва).
Проверить наличие вертикальных асимптот в точках разрыва и на границах области определения.
Найти точки пересечения с осями координат.
Найти нули функции. Найти интервалы знакопостоянства функции.
Установить, является ли функция чётной или нечётной. Сделать выводы о симметричности графика функции.
Установить, является ли функция периодической или нет. Обычно проверяют для тригонометрических функций, для других данный пункт пропускается.
Построить график элементарной функции, а затем способом преобразования графиков построить график данной функции.
Способы преобразования графиков.
| Алгоритм 1. (построение графика функции y = f(x+l) + m ) |
| Алгоритм 2. (построение графика функции y = f(x+l) + m ) |
Правило: чтобы построить график функции ![]() , где
, где ![]() , нужно график функции
, нужно график функции ![]() сжать к оси
сжать к оси ![]() в
в ![]() раз.
раз.
Правило: чтобы построить график функции ![]() , где
, где ![]() , нужно график функции
, нужно график функции ![]() растянуть от оси
растянуть от оси ![]() в
в ![]() раз.
раз.
Правило: чтобы построить график функции ![]() , нужно график
, нужно график ![]() отобразить симметрично относительно оси
отобразить симметрично относительно оси ![]() .
.
2.Примеры выполнения заданий.
Сжатие графика функции к оси ординат
Пример 1
Построить график функции ![]() .
.
Сначала изобразим график синуса, его период равен ![]() :
:
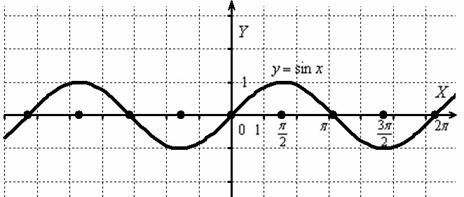
К слову, чертить графики тригонометрических функций вручную – занятие кропотливое, поскольку ![]() и т.д., то есть на стандартной клетчатой бумаге аккуратным нужно быть вплоть до миллиметра, даже до полумиллиметра. Впрочем, многие с этим уже столкнулись.
и т.д., то есть на стандартной клетчатой бумаге аккуратным нужно быть вплоть до миллиметра, даже до полумиллиметра. Впрочем, многие с этим уже столкнулись.
Мысленно возьмём синусоиду в руки и сожмём её к оси ![]() в 2 раза:
в 2 раза:
То есть, график функции ![]() получается путём сжатия графика
получается путём сжатия графика ![]() к оси ординат в два раза. Логично, что период итоговой функции тоже уполовинился:
к оси ординат в два раза. Логично, что период итоговой функции тоже уполовинился: ![]()
В целях самоконтроля можно взять 2-3 значения «икс» и устно либо на черновике выполнить подстановку:
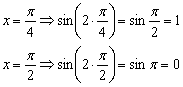
Смотрим на чертёж, и видим, что это действительно так.
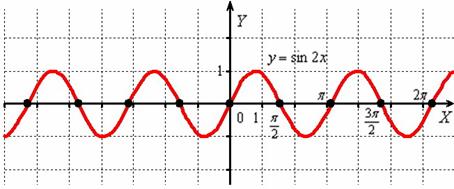
Пример 2
Построить график функции ![]()
![]() сжимается к оси
сжимается к оси ![]() в 3 раза:
в 3 раза:
Итоговый график ![]() проведён красным цветом.
проведён красным цветом.
Исходный период ![]() косинуса закономерно уменьшается в три раза:
косинуса закономерно уменьшается в три раза: ![]() (отграничен жёлтыми точками).
(отграничен жёлтыми точками).
Случай имеет место, когда АРГУМЕНТ функции умножается на число ![]() .
.
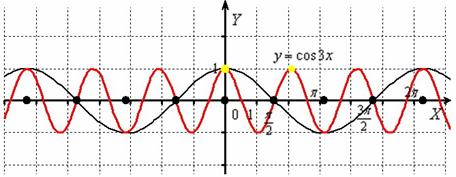
Пример 3
Построить график функции ![]()
Растягиваем y=sinx от оси ![]() в 2 раза:
в 2 раза:
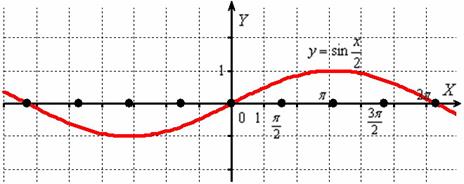
То есть, график функции ![]() получается путём растяжения графика
получается путём растяжения графика ![]() от оси ординат в два раза. Период итоговой функции увеличивается в 2 раза:
от оси ординат в два раза. Период итоговой функции увеличивается в 2 раза: ![]() , он толком даже не вместился на данный чертёж.
, он толком даже не вместился на данный чертёж.
Операции сжатия/растяжения графиков, разумеется, выполнимы не только для тригонометрических функций:
Пример 4
Построить графики функций ![]()
График функции ![]() получается путём сжатия графика экспоненты
получается путём сжатия графика экспоненты ![]() к оси
к оси ![]() в два раза. А график
в два раза. А график ![]() – путём растяжения графика экспоненты
– путём растяжения графика экспоненты ![]() от оси
от оси ![]() в два раза:
в два раза:
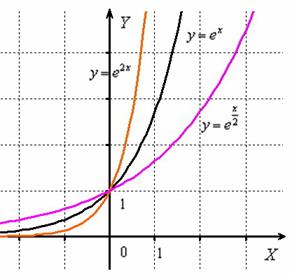
АРГУМЕНТ функции меняет знак.
Пример 5
Построить график функции ![]()
График функции ![]() получается путём симметричного отображения графика
получается путём симметричного отображения графика ![]() относительно оси ординат:
относительно оси ординат:
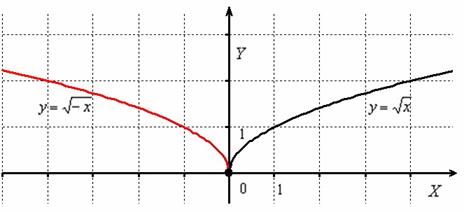
Как видите, всё просто.
Если при умножении аргумента на число ![]() значение параметра
значение параметра ![]() отрицательно и не равно минус единице, то построение выполняется в два шага. Например:
отрицательно и не равно минус единице, то построение выполняется в два шага. Например: ![]() . На первом шаге выполняем сжатие графика
. На первом шаге выполняем сжатие графика ![]() к оси ординат в 2 раза:
к оси ординат в 2 раза: ![]() . На втором шаге график
. На втором шаге график ![]() отображаем симметрично относительно оси ординат:
отображаем симметрично относительно оси ординат: ![]() . Конкретный пример обязательно рассмотрим ниже.
. Конкретный пример обязательно рассмотрим ниже.
Пример 6
Построить график функции ![]()
Берём параболу ![]() и сдвигаем её вдоль оси абсцисс на 1 единицу вправо:
и сдвигаем её вдоль оси абсцисс на 1 единицу вправо:
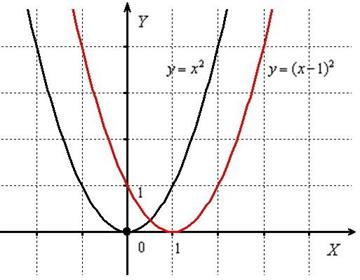
«Опознавательным маячком» служит значение ![]() , именно здесь находится вершина параболы
, именно здесь находится вершина параболы ![]() .
.
Теперь, думаю, ни у кого не возникнет трудностей с построением графика ![]() (демонстрационный пример начала урока) – кубическую параболу
(демонстрационный пример начала урока) – кубическую параболу ![]() нужно сдвинуть на 2 единицы влево.
нужно сдвинуть на 2 единицы влево.
Вот ещё один характерный случай:
Пример 7
Построить график функции ![]()
Гиперболу ![]() (чёрный цвет) сдвинем вдоль оси
(чёрный цвет) сдвинем вдоль оси ![]() на 2 единицы влево:
на 2 единицы влево:
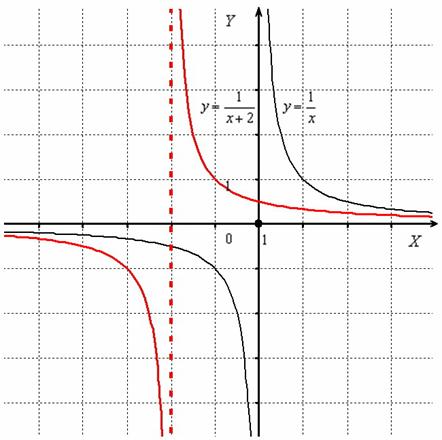
Перемещение гиперболы «выдаёт» значение, которое не входит в область определения функции. В данном примере ![]() , и уравнение прямой
, и уравнение прямой ![]() задаёт вертикальную асимптоту (красный пунктир) графика функции
задаёт вертикальную асимптоту (красный пунктир) графика функции ![]() (красная сплошная линия). Таким образом, при параллельном переносе асимптота графика тоже сдвигается (что очевидно).
(красная сплошная линия). Таким образом, при параллельном переносе асимптота графика тоже сдвигается (что очевидно).
Вернёмся к тригонометрическим функциям:
Пример 8
Построить график функции ![]()
График синуса ![]() (чёрный цвет) сдвинем вдоль оси вдоль оси
(чёрный цвет) сдвинем вдоль оси вдоль оси ![]() на
на ![]() влево:
влево:
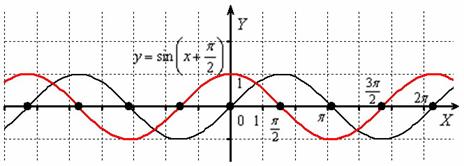
Внимательно присмотримся к полученному красному графику ![]() …. Это в точности график косинуса
…. Это в точности график косинуса ![]() ! По сути, мы получили геометрическую иллюстрацию формулы приведения
! По сути, мы получили геометрическую иллюстрацию формулы приведения ![]() , и перед вами, пожалуй, самая «знаменитая» формула, связывающая данные тригонометрические функции. График функции
, и перед вами, пожалуй, самая «знаменитая» формула, связывающая данные тригонометрические функции. График функции ![]() получается путём сдвига синусоиды
получается путём сдвига синусоиды ![]() вдоль оси
вдоль оси ![]() на
на ![]() единиц влево. Рассмотрим композиционное правило, когда аргумент представляет собой линейную функцию:
единиц влево. Рассмотрим композиционное правило, когда аргумент представляет собой линейную функцию: ![]() , при этом параметр «ка» не равен нулю или единице, параметр «бэ» – не равен нулю. Как построить график такой функции? Из школьного курса мы знаем, что, что умножение имеет приоритет перед сложением, поэтому, казалось бы, сначала график сжимаем/растягиваем/отображаем в зависимости от значения
, при этом параметр «ка» не равен нулю или единице, параметр «бэ» – не равен нулю. Как построить график такой функции? Из школьного курса мы знаем, что, что умножение имеет приоритет перед сложением, поэтому, казалось бы, сначала график сжимаем/растягиваем/отображаем в зависимости от значения ![]() , а потом сдвигаем на
, а потом сдвигаем на ![]() единиц. Но здесь есть подводный камень, и корректный алгоритм таков:
единиц. Но здесь есть подводный камень, и корректный алгоритм таков:
Аргумент функции необходимо представить в виде ![]() и последовательно выполнить следующие преобразования:
и последовательно выполнить следующие преобразования:
1) График функции ![]() сжимаем (или растягиваем) к оси (от оси) ординат:
сжимаем (или растягиваем) к оси (от оси) ординат:![]() (если
(если ![]() , то график дополнительно следует отобразить симметрично относительно оси
, то график дополнительно следует отобразить симметрично относительно оси ![]() ).
).
2) График полученной функции ![]() сдвигаем влево (или вправо) вдоль оси абсцисс на
сдвигаем влево (или вправо) вдоль оси абсцисс на ![]() (!!!) единиц, в результате чего будет построен искомый график
(!!!) единиц, в результате чего будет построен искомый график ![]() .
.
Пример 9
Построить график функции ![]()
Представим функцию в виде ![]() и выполним следующие преобразования: синусоиду
и выполним следующие преобразования: синусоиду ![]() (чёрный цвет):
(чёрный цвет):
1) сожмём к оси ![]() в два раза:
в два раза:![]() (синий цвет);
(синий цвет);
2) сдвинем вдоль оси ![]() на
на ![]() (!!!) влево:
(!!!) влево: ![]() (красный цвет):
(красный цвет):
Пример вроде бы несложный, а пролететь с параллельным переносом легче лёгкого. График сдвигается на ![]() , а вовсе не на
, а вовсе не на ![]() .
.
Продолжаем расправляться с функциями начала урока:
Пример 10
Построить график функции ![]()
Представим функцию в виде ![]() . В данном случае:
. В данном случае: ![]() Построение проведём в три шага. График натурального логарифма
Построение проведём в три шага. График натурального логарифма ![]() :
:
1) сожмём к оси ![]() в 2 раза:
в 2 раза: ![]() ;
;
2) отобразим симметрично относительно оси ![]() :
: ![]() ;
;
3) сдвинем вдоль оси ![]() на
на ![]() (!!!) вправо:
(!!!) вправо: ![]() :
:
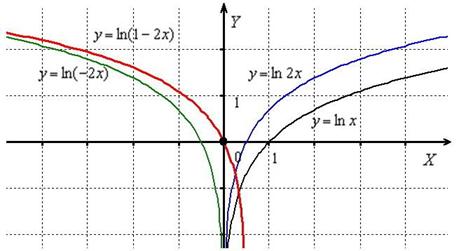
Для самоконтроля в итоговую функцию ![]() можно подставить пару значений «икс», например,
можно подставить пару значений «икс», например, ![]() и свериться с полученным графиком.
и свериться с полученным графиком.
Симметричное отображение графика относительно оси абсцисс
1) Если ФУНКЦИЯ ![]() умножается на число
умножается на число ![]() , то происходит растяжение её графика вдоль оси ординат.
, то происходит растяжение её графика вдоль оси ординат.
Правило: чтобы построить график функции ![]() , где
, где ![]() , нужно график функции
, нужно график функции ![]() растянуть вдоль оси
растянуть вдоль оси ![]() в
в ![]() раз.
раз.
2) Если ФУНКЦИЯ умножается на число ![]() , то происходит сжатие её графика вдоль оси ординат.
, то происходит сжатие её графика вдоль оси ординат.
Правило: чтобы построить график функции ![]() , где
, где ![]() , нужно график функции
, нужно график функции ![]() сжать вдоль оси
сжать вдоль оси ![]() в
в ![]() раз.
раз.
Пример 11
Построить графики функций ![]() .
.
Берём синусоиду за макушку/пятки:

И вытягиваем её вдоль оси ![]() в 2 раза:
в 2 раза:
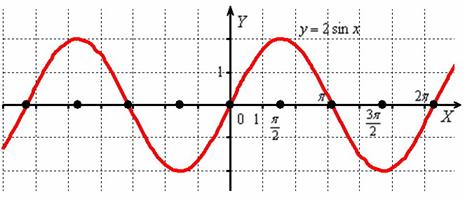
Период функции ![]() не изменился и составляет
не изменился и составляет ![]() , а вот значения (все, кроме нулевых) увеличились по модулю в два раза, что логично – ведь функция умножается на 2, и область её значений удваивается:
, а вот значения (все, кроме нулевых) увеличились по модулю в два раза, что логично – ведь функция умножается на 2, и область её значений удваивается: ![]() .
.
Теперь сожмём синусоиду вдоль оси ![]() в 2 раза:
в 2 раза:
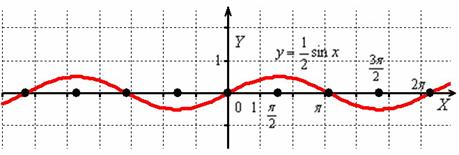
Аналогично, период ![]() не изменился, но область значений функции «сплющилась» в два раза:
не изменился, но область значений функции «сплющилась» в два раза: ![]() .
.
И, конечно же, классический пример растяжения/сжатия параболы:
Пример 12
Построить графики функций ![]() .
.
Возьмём рога молодого оленя ![]() и вытянем их вверх вдоль оси
и вытянем их вверх вдоль оси ![]() в два раза:
в два раза: ![]() . Затем сожмём
. Затем сожмём ![]() вдоль оси ординат в 2 раза:
вдоль оси ординат в 2 раза: ![]()
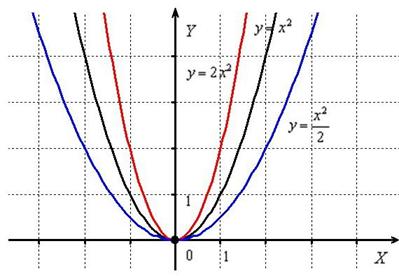
И снова заметьте, что значения функции ![]() увеличиваются в 2 раза, а значения
увеличиваются в 2 раза, а значения ![]() уменьшаются во столько же раз (исключение составляет точка
уменьшаются во столько же раз (исключение составляет точка ![]() ).
).
Отпустим в тундру удивлённое животное и продолжим изучать умножение функции на число: ![]() . Случаи
. Случаи ![]() не представляют интереса, поэтому рассмотрим отрицательные коэффициенты. Сначала распространённый частный случай
не представляют интереса, поэтому рассмотрим отрицательные коэффициенты. Сначала распространённый частный случай ![]() :
:
Если ФУНКЦИЯ меняет знак на противоположный, то её график отображается симметрично относительно оси абсцисс.
Правило: чтобы построить график функции ![]() , нужно график
, нужно график ![]() отобразить симметрично относительно оси
отобразить симметрично относительно оси ![]() .
.
Пример 13
Построить график функции ![]()
Отобразим синусоиду симметрично относительно оси ![]() :
:
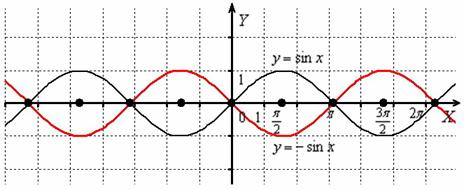
Ещё более наглядно симметрия просматривается у следующей типовой функции:
Пример 14
Построить график функции ![]()
График функции ![]() получается путём симметричного отображения графика
получается путём симметричного отображения графика ![]() относительно оси абсцисс:
относительно оси абсцисс:
Функции ![]() задают две ветви параболы, которая «лежит на боку». Обратная функция
задают две ветви параболы, которая «лежит на боку». Обратная функция ![]() задаёт параболу целиком
задаёт параболу целиком
Если к ФУНКЦИИ добавляется константа, то происходит сдвиг (параллельный перенос) её графика вдоль оси ![]() . Рассмотрим функцию
. Рассмотрим функцию ![]() и положительное число
и положительное число ![]() :
:
Правила:
1) чтобы построить график функции ![]() , нужно график
, нужно график ![]() сдвинуть ВДОЛЬ оси
сдвинуть ВДОЛЬ оси ![]() на
на ![]() единиц вверх;
единиц вверх;
2) чтобы построить график функции ![]() , нужно график
, нужно график ![]() сдвинуть ВДОЛЬ оси
сдвинуть ВДОЛЬ оси ![]() на
на ![]() единиц вниз.
единиц вниз.
Пример 15
Построить графики функций ![]() .
.
В комментариях, думаю, нет особой необходимости:
Комбинационное построение графика ![]() в общем случае осуществляется очевидным образом:
в общем случае осуществляется очевидным образом:
1) График функции ![]() растягиваем (сжимаем) вдоль оси
растягиваем (сжимаем) вдоль оси ![]() . Если множитель отрицателен, дополнительно осуществляем симметричное отображение относительно оси
. Если множитель отрицателен, дополнительно осуществляем симметричное отображение относительно оси ![]() .
.
2) Полученный на первом шаге график ![]() сдвигаем вверх или вниз в соответствии со значением константы
сдвигаем вверх или вниз в соответствии со значением константы ![]() .
.
Пример 16
Построить график функции ![]()
График косинуса ![]() (чёрный цвет):
(чёрный цвет):
1) Растягиваем вдоль оси ![]() в 1,5 раза:
в 1,5 раза: ![]() (синий цвет);
(синий цвет);
2) Сдвигаем вдоль оси ![]() на 2 единицы вниз:
на 2 единицы вниз: ![]() :
:
Простой, но весьма распространённый кадр:
Пример 17
Построить график функции ![]()
Параболу ![]() :
:
1) отобразим симметрично относительно оси абсцисс: ![]() ;
;
2) сдвинем вдоль оси ![]() на 4 единицы вверх:
на 4 единицы вверх: ![]() :
:
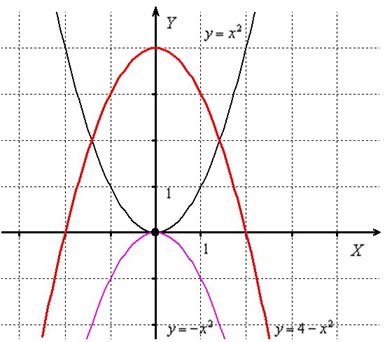
Да, конечно, данную кривую легко построить и поточечно, но такие параболы очень часто встречаются в практических заданиях, поэтому весьма полезно сразу представлять, как они расположены.
Аналогичный трехходовой пример с растяжением и симметричным отображением графика относительно оси ![]() :
:
Пример 18
Построить график функции ![]()
График экспоненциальной функции ![]() :
:
1) растянем вдоль оси ![]() в 2 раза:
в 2 раза: ![]() ;
;
2) отобразим симметрично относительно оси абсцисс: ![]() ;
;
3) сдвинем вдоль оси ![]() на 1 единицу вверх:
на 1 единицу вверх: ![]() :
:
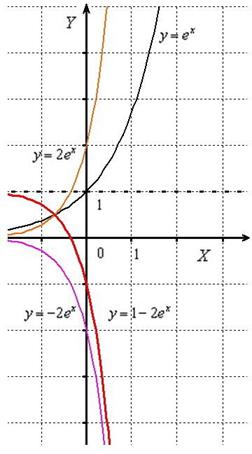
Заметьте, что в результате последнего преобразования горизонтальная асимптота графика тоже «уехала» вверх на 1 единицу. Аналогичный факт мы уже наблюдали при сдвиге гиперболы (см. Пример №7).
Систематизируем всю информацию:
с помощью геометрических преобразований
Рассмотрим функцию ![]() , которая «базируется» на некоторой функции
, которая «базируется» на некоторой функции ![]() . Для многих читателей алгоритм построения графика уже понятен:
. Для многих читателей алгоритм построения графика уже понятен:
– на первом шаге выполняем преобразования, связанные с АРГУМЕНТОМ функции (см. первые два параграфа), в результате чего получаем график функции ![]() ;
;
– на втором шаге выполняем только что рассмотренные преобразования, связанные с самой ФУНКЦИЕЙ, и получаем график ![]() .
.
Завершим самое длинное построение данного урока:
Пример 19 (концовка Примера 10)
Построить график функции ![]()
В примере №10 мы выполнили построение графика ![]() , то есть полностью разобрались с аргументом функции. И сейчас осталось выполнить завершающие шаги.
, то есть полностью разобрались с аргументом функции. И сейчас осталось выполнить завершающие шаги.
График функции ![]() :
:
4) отобразим симметрично относительно оси ![]() :
: ![]() ;
;
5) сдвинем вдоль оси ![]() на 3 единицы вверх:
на 3 единицы вверх: ![]() :
:
На практике, к счастью, построения почти всегда более коротки, например:
![]() – кубическую параболу
– кубическую параболу ![]() сдвигаем вдоль оси
сдвигаем вдоль оси ![]() на 5 единиц вправо и сжимаем вдоль оси
на 5 единиц вправо и сжимаем вдоль оси ![]() в 3 раза.
в 3 раза.
![]() – график экспоненты отображаем симметрично относительно оси ординат, затем – симметрично относительно оси абсцисс.
– график экспоненты отображаем симметрично относительно оси ординат, затем – симметрично относительно оси абсцисс.
![]() – график функции
– график функции ![]() смещаем влево на 5 единиц, затем – вверх на 1 единицу.
смещаем влево на 5 единиц, затем – вверх на 1 единицу.
Пример 20
Построить график функции ![]() с помощью преобразований графиков элементарных функций
с помощью преобразований графиков элементарных функций
Идея состоит в том, чтобы искусственно преобразовать функцию ТАК, чтобы воспользоваться одной из формул сокращенного умножения ![]() либо
либо ![]() .
.
Начнём преобразования. Коэффициент при ![]() выносим за скобку:
выносим за скобку:
![]()
Очевидно, что выражение сведётся к формуле ![]() . В скобках конструируем
. В скобках конструируем ![]() :
:
![]()
Таким образом, ![]() . Теперь организуем
. Теперь организуем ![]() , для этого в скобках прибавим и вычтем
, для этого в скобках прибавим и вычтем ![]() :
:
![]()
Последнее слагаемое выносим из скобок:
![]()
Используем формулу ![]() и суммируем два последних слагаемых:
и суммируем два последних слагаемых:
![]()
В целях проверки целесообразно раскрыть скобки и убедиться, что получится исходная функция:
![]()
Построим график ![]() . Параболу
. Параболу ![]() :
:
1) Сдвинем вдоль оси ![]() на
на ![]() влево:
влево: ![]() (синий цвет);
(синий цвет);
2) Вытянем вдоль оси ![]() в 2 раза:
в 2 раза: ![]() (малиновый цвет);
(малиновый цвет);
3) Сдвинем вдоль оси ![]() на
на ![]() вверх:
вверх: ![]() (красный цвет):
(красный цвет):
Рассмотрим ещё один типовой трюк:
Пример 21
Построить график функции ![]() с помощью преобразований графиков элементарных функций.
с помощью преобразований графиков элементарных функций.
Сначала сведём функцию к виду ![]() . Все действия я закомментирую:
. Все действия я закомментирую:
![]()
(1) В знаменателе выносим –1 за скобки. Это необходимо, чтобы аргумент функции представить «в привычном» порядке ![]() .
.
(2) Минус знаменателя поставим перед дробью. В числителе проведём искусственное преобразование – прибавим и вычтем единицу. Это необходимо для почленного деления на следующем шаге.
(3) Почленно делим числитель на знаменатель.
(4) Раскрываем скобки.
Проведём построение. График гиперболы ![]() (чёрный цвет):
(чёрный цвет):
1) Сдвинем вправо на 1 единицу: ![]() (синий цвет);
(синий цвет);
2) Отобразим симметрично относительно оси абсцисс: ![]() (малиновый цвет);
(малиновый цвет);
3) Сдвинем вдоль оси ![]() на единицу вниз:
на единицу вниз: ![]() (красный цвет):
(красный цвет):
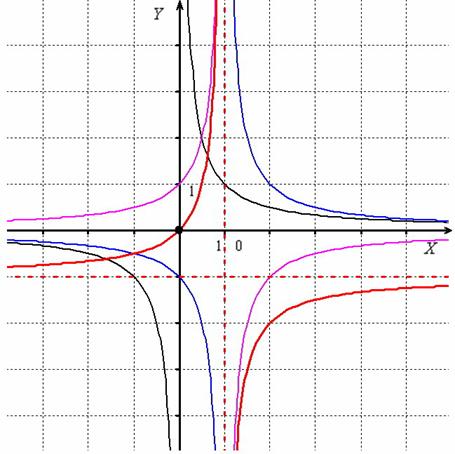
Самостоятельное выполнение задания.
В-1.
1. Описать свойства и построить график функции y=x6
2. Построив график функции y=5x, постройте график функции y=5x+3.
B-2.
1. Описать свойства и построить график функции y=x5
2. Построив график функции y= 3x . Построить график функции y= 3x-2.
B-3.
1. Описать свойства и построить график функции ![]() .
.
2. Построив график функции y= sin x. Построить график функции y= sin x+1.
B-4.
1. Описать свойства и построить график функции ![]() .
.
2. Построив график функции y=2х. постройте график функции y=2x-5.
B-5.
Описать свойства и построить график функции ![]() .
.
2. Построив график функции y=![]() . Построить график функции y=
. Построить график функции y=![]() +4.
+4.
B-6.
1. Описать свойства и построить график функции ![]() .
.
2. Построив график функции y= cosx. Построить график функции y= cosx-2.
B-7.
1. Описать свойства и построить график функции ![]() .
.
2. Построив график функции y=3х. постройте график функции y= 3(x+2).
B-8.
1. Описать свойства и построить график функции ![]() .
.
2. Построив график функции y=![]() . Построить график функции y=
. Построить график функции y=![]() -1.
-1.
B-9.
1. Описать свойства и построить график функции ![]() .
.
2. Построив график функции y=sin x. Построить график функции y=sin(x-![]() )
)
B-10.
1. Описать свойства и построить график функции ![]() .
.
2. Построив график функции y=2х. постройте график функции y=2(x-3).
---------------------------------------------------------------------------------------------------
B-11.
1. Описать свойства и построить график функции ![]() .
.
2. Построив график функции y=![]() . Построить график функции y=
. Построить график функции y=![]() +2.
+2.
B-12.
1. Описать свойства и построить график функции ![]() .
.
2. Построив график функции y=х2. постройте график функции y=x2+2.
B-13.
1. Описать свойства и построить график функции ![]() .
.
2. Построив график функции y= 2x. Построить график функции y= 2x+1
B-14.
1. Описать свойства и построить график функции ![]() .
.
2. Построив график функции y=х2. постройте график функции y= x2-3.
B-15.
1. Описать свойства и построить график функции ![]() .
.
2. Построив график функции ![]() . Построить график функции
. Построить график функции ![]()
4. сделать вывод.
ПРАКТИЧЕСКАЯ РАБОТА №9
по учебной дисциплине «Математика»
Тема: Вычисление табличных производных, составление уравнений касательной и нормали к графику функции.
Цель: Научиться вычислять табличные производные, составлять уравнения касательной и нормали к графику функции.
Оборудование: 1) Методическое пособие по выполнению работы
2) Учебник Математика ДадаянА.А.
3) Учебник Математика Башмаков М.И.
Время выполнения: Повторение теоретического материала – 12 минут, решение по образцу – 18 минут, самостоятельное выполнение заданий – 60 минут.
Ход работы:
Повторение теоретического материала.
Таблица производных основных элементарных функций.
1. (c)/=0 (c- константа) 2. ![]()
3.![]() 4.
4.![]()
5. ![]() 6.
6. ![]()
7. ![]() 8.
8. ![]()
9. ![]() 10.
10. ![]()
11. ![]() 12.
12. ![]()
13. ![]() 14.
14. ![]()
15. ![]() 16.
16. ![]()
Правила вычисления производных:
1. ![]() с - постоянная
с - постоянная
Постоянный множитель можно выносить за знак производной.
2. ![]()
Производная суммы дифференцируемых функций равна сумме их производных.
3.![]() - производная произведения.
- производная произведения.
4. ![]() - производная частного.
- производная частного.
5. ![]() - производная сложной функции.
- производная сложной функции.
Примеры выполнения заданий.
Найдите производные следующих функций: а) y=2x-5 ; б)y=4x1/3 +5x-2/5;
в)y=![]() г)y=sin(5x+x2)
г)y=sin(5x+x2)
a)Воспользуемся следствием (постоянный множитель можно выносить за знак производной) и формулой 4 из таблицы производных, получим: ![]()
б) Воспользуемся правилом 2, следствием и формулой 4 из таблицы производных: ![]()
в) Воспользуемся правилом 3 и формулами 9 и 5 из таблицы производных :![]()
г) Воспользуемся правилом 5,2, следствием и формулами 4 и 17 таблицы производных: ![]()
3. Самостоятельное выполнение заданий.
Вариант №1
1. Найдите производную функций:
1) f(x) = ctg x +2x3 – 2x , 2) f(x) = x2 sinx, 3) f(x) =![]() ,
,
4) f(x) = (3x2 – 2tgx)5, 5) f(x) = ![]()
![]() - 3x +
- 3x + ![]() - 10.
- 10.
6) f(x)=![]() 7) f(x)=3sin2x – 2cos3x
7) f(x)=3sin2x – 2cos3x
Дополнительное задание.
2. Точка движется по закону S = 3t3 – 12t +5. Найдите скорость движения при t = 2с.
3. Определите угловой коэффициент касательной, проведенной к кривой
у = 3cosx+sinx в точке х0 = п.
Вариант №2
1. Найдите производную функций:
1) f(x) =![]() - x +
- x + ![]() + 8
+ 8![]() , 2) f(x) = (x2 – 2sinx)3, 3) f(x) =
, 2) f(x) = (x2 – 2sinx)3, 3) f(x) =![]() ,
,
4) f(x) = x 2 tgx, 5) f(x) = 5cos x +x5 – ex .
6) f(x)=x3+cos x. 7) f(x)=3 4x +x2
Дополнительное задание.
2. Точка движется по закону S =2t3 + t -5. Найдите скорость движения при t = 3с.
3. Определите угловой коэффициент касательной, проведенной к кривой у = ex + lnx в точке х0 = 1.
Вариант №3
1. Найдите производную функций:
1) f(x) =![]() , 2) f(x) = (x – 5cosx)3,3) f(x) =
, 2) f(x) = (x – 5cosx)3,3) f(x) =![]() - 2x9 +
- 2x9 + ![]() - 2,
- 2,
4) f(x) = x 7 ctgx, 5) f(x) = sin x - 2x7 – 6x .
6) f(x)=2x – sin x. 7) f(x)= 4e 5x – 7x3
Дополнительное задание.
2. Точка движется по закону S = 5t3 – 8t +3. Найдите скорость движения при t = 1с. 3. Определите угловой коэффициент касательной, проведенной к кривой у = 3tgx- cosx в точке х0 = п.
1. Найдите производную функций:
1) f(x) = cos x +6x4 – 4x , 2) f(x) = x 3 ctgx, 3) f(x) =![]() ,
,
4) f(x) = (2x3 – 5lnx)3, 5) f(x) = ![]()
![]() - 3x +
- 3x + ![]() +1.
+1.
6) f(x)=2x + 1 7) f(x)=sin(x+x3) - ![]() .
.
Дополнительное задание.
2. Точка движется по закону S = 2t3 – 2t +5. Найдите скорость движения при t = 3с.
3. Определите угловой коэффициент касательной, проведенной к кривой
у = 3log 2 x-5 в точке х0 = 3.
Вариант №5
1. Найдите производную функций:
1) f(x) =![]() - x7 +
- x7 + ![]() -
- ![]() , 2) f(x) = (5x – 4cosx)5, 3) f(x) =
, 2) f(x) = (5x – 4cosx)5, 3) f(x) =![]() ,
,
4) f(x) = x 2 tgx, 5) f(x) = 5sin x +x6 – 8ex .
6) f(x)=cos x – x 7) f(x)= -ex + 3x3x
Дополнительное задание.
2. Точка движется по закону S = t3 – 4t . Найдите скорость движения при t = 2с.
3. Определите угловой коэффициент касательной, проведенной к кривой
у = 3(x3 +5) в точке х0 = 2.
Вариант №6
1. Найдите производную функций:
1) f(x) =![]() , 2) f(x) = (x2 – ex)5, 3) f(x) =
, 2) f(x) = (x2 – ex)5, 3) f(x) =![]() - 5x4 +
- 5x4 + ![]() - 3,
- 3,
4) f(x) = x 5 lnx, 5) f(x) = ![]() - x2 – 2x
- x2 – 2x
6 f(x)=x5 – sin x 7) f(x)=x4 + cos(x+3x2)
Дополнительное задание.
2. Точка движется по закону S = t3 + 12t -5. Найдите скорость движения при t = 2с.
3. Определите угловой коэффициент касательной, проведенной к кривой
у = 3/x в точке х0 = 3.
ПРАКТИЧЕСКАЯ РАБОТА №10
по учебной дисциплине «Математика»
Тема: Применение производной к исследованию функций и построению графиков.
Цель: Научиться применять производную к исследованию функции и построению её графика.
Оборудование: 1) Методическое пособие по выполнению работы
2) Учебник Математика ДадаянА.А.
3) Учебник Математика Башмаков М.И.
Время выполнения: Повторение теоретического материала – 12 минут, решение по образцу – 18 минут, самостоятельное выполнение заданий – 60 минут.
Ход работы:
Повторение теоретического материала.
Схема исследования функции и построение её графика.
Найти область определения функции.
Найти область значений функции. Обычно этот пункт пропускают или заполняют после исследования на экстремумы.
Исследовать непрерывность функции, выделить особые точки (точки разрыва).
Проверить наличие вертикальных асимптот в точках разрыва и на границах области определения.
Найти точки пересечения с осями координат.
Найти нули функции. Найти интервалы знакопостоянства функции.
Установить, является ли функция чётной или нечётной. Сделать выводы о симметричности графика функции.
Установить, является ли функция периодической или нет. Обычно проверяют для тригонометрических функций, для других данный пункт пропускается.
Найти первую производную. Найти точки экстремума (локального минимума и максимума) и интервалы монотонности (возрастания и убывания) функции.
Найти вторую производную. Найти точки перегиба и интервалы выпуклости-вогнутости.
Найти наклонные/горизонтальные асимптоты функции.
Исследовать поведение функции на бесконечности.
Построить график функции. Построить асимптоты.
Отметить важные точки на графике.
Пример выполнения задания.
Исследовать функцию и построить график:
![]()
Решение:
1) Область определения функции: ![]()
2) ![]()
Функция не является четной, нечетной, периодической
3) График функции пересекает оси координат в точке (0, 0)
4) ![]()
В точке ![]() существует разрыв 2-го рода.
существует разрыв 2-го рода.
Прямая ![]() – вертикальная асимптота.
– вертикальная асимптота.
Для нахождения наклонной асимптоты вычисляем пределы:
![]()
![]()
У=0–горизонтальная асимптота
5) Исследуем функцию на экстремум. Найдем производную функции.
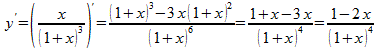
Приравняем найденную производную к нулю и решим полученное уравнение:
![]()
![]() -функция возрастает
-функция возрастает
![]() -функция возрастает
-функция возрастает
![]() -функция убывает
-функция убывает
![]() -точка максимума
-точка максимума
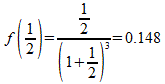
6) Исследуем функцию на интервалы выпуклости и вогнутости.
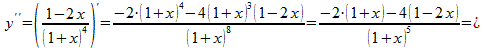
![]()
Приравняем найденную производную к нулю и решим полученное уравнение:
![]()
![]() -график функции вогнутый
-график функции вогнутый
![]() -график функции выпуклый
-график функции выпуклый
![]() -график функции вогнутый
-график функции вогнутый
![]() -точка перегиба
-точка перегиба
![]()
7) График функции имеет вид:
Самостоятельное выполнение задания.
Вариант-1
1.Исследуйте на монотонность, экстремумы и постройте график функции
у = Х3 .
2(х+1)2.
2. Точка движется по закону S = 3t3 – 12t +5. Найдите скорость движения при t = 2с.
Вариант №2
1. Исследуйте на монотонность, экстремумы и постройте график функции
у = Х3+4 .
Х2
2. Точка движется по закону S =-2t3 + t -5. Найдите скорость движения при t = 3с.
Вариант №3
1. Исследуйте на монотонность, экстремумы и постройте график функции
у =х + 1 .
2х
2. Точка движется по закону S = 5t3 – 8t +3. Найдите скорость движения при t = 1с. Вариант №41. Исследуйте на монотонность, экстремумы и постройте график функции
у = _2х .
1 - х2
2. Точка движется по закону S = 2t3 – 2t +5. Найдите скорость движения при t = 3с.
Вариант №5
1. Исследуйте на монотонность, экстремумы и постройте график функции
у = еХ .
х-1
2. Точка движется по закону S = t3 – 11t . Найдите скорость движения при t = 2с.
Вариант №6
1. Исследуйте на монотонность, экстремумы и постройте график функции
у = Х2 – 9_ .
Х2 - 4
2. Точка движется по закону S =- t3 + 12t -5. Найдите скорость движения при t = 2с.
4. Сделать вывод
5.ЗАКЛЮЧЕНИЕ.
Проведенный мною теоретический анализ показал, что:
Практические работы являются обязательным и необходимым элементом при изучении курса «Математика»;
Практические работы позволяют закреплять теоретический материал и совершенствовать практические навыки;
Практические работы способствуют развитию общеучебных умений: анализировать, сравнивать, сопоставлять, оценивать, делать умозаключения, высказывать собственное мнение и обосновывать его, свертывать информацию, представлять результаты работы в различных формах: выводах, тезисах, логических схемах, таблицах и др.
Практическая работа отвечает определенным требованиям и имеет определенную структуру;
В практической части методической разработки представлена методика выполнения практических работ.
68