5. Разложение многочлена на множители.

5. Разложение многочлена на множители.

Преобразование многочлена в произведение двух и более многочленов, среди которых могут быть и одночлены, называется разложением на множители.

Существует 5 основных способов разложения многочлена на множители:

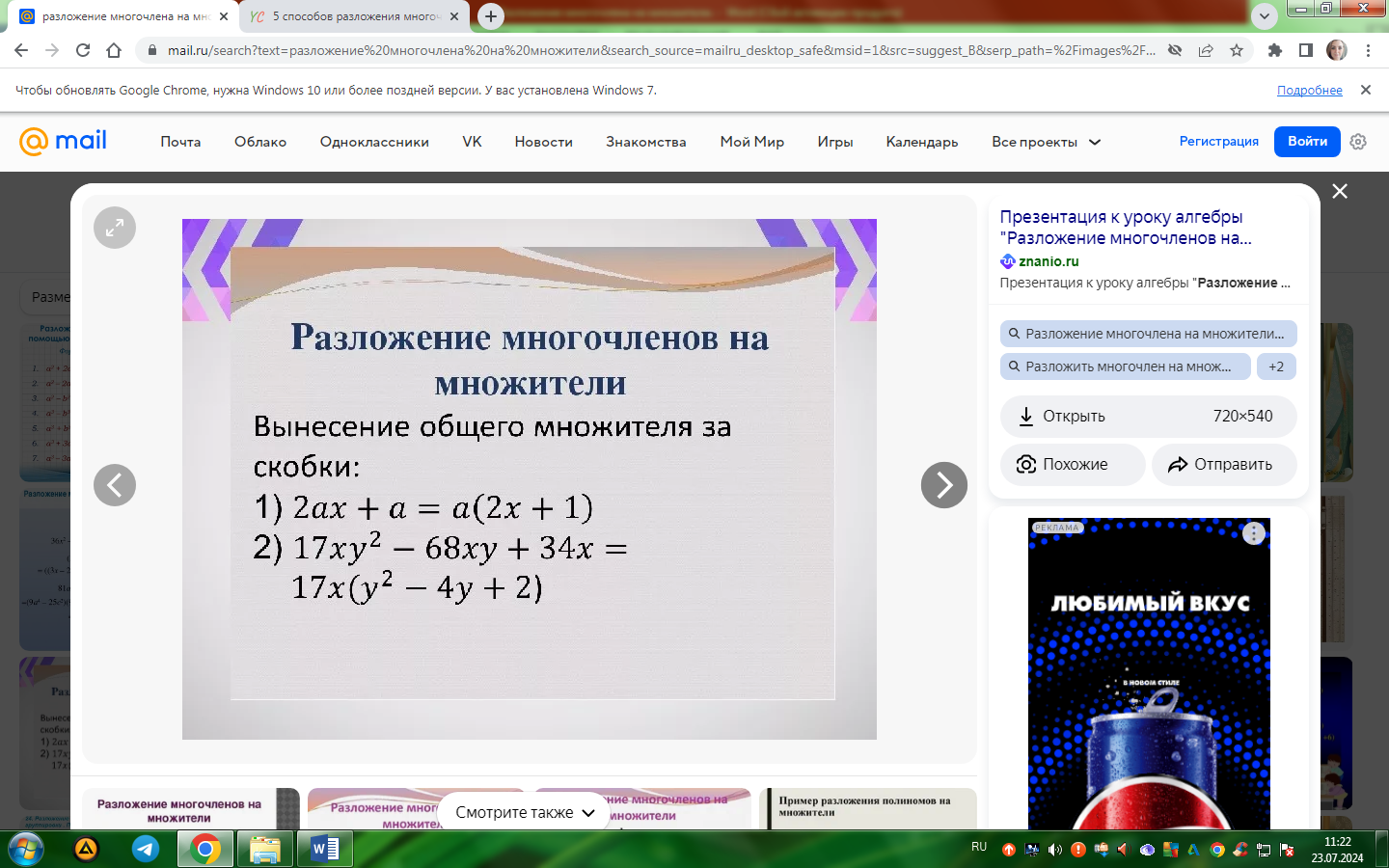
• вынесение общего множителя за скобки;

• использование формул сокращенного умножения, метод выделения полного квадрата;

• метод группировки;

• разложение квадратного трехчлена на множители.

• Деление многочлена на линейный двучлен.

Разложение многочлена на множители – тождественное преобразование, превращающее сумму в произведение нескольких множителей. При этом каждый множитель может быть как многочленом, так и одночленом.

Для чего нужно знать все пять способов? Потому что нет универсального способа, подходящего для всех многочленов.

1. Вынесение общего множителя за скобки

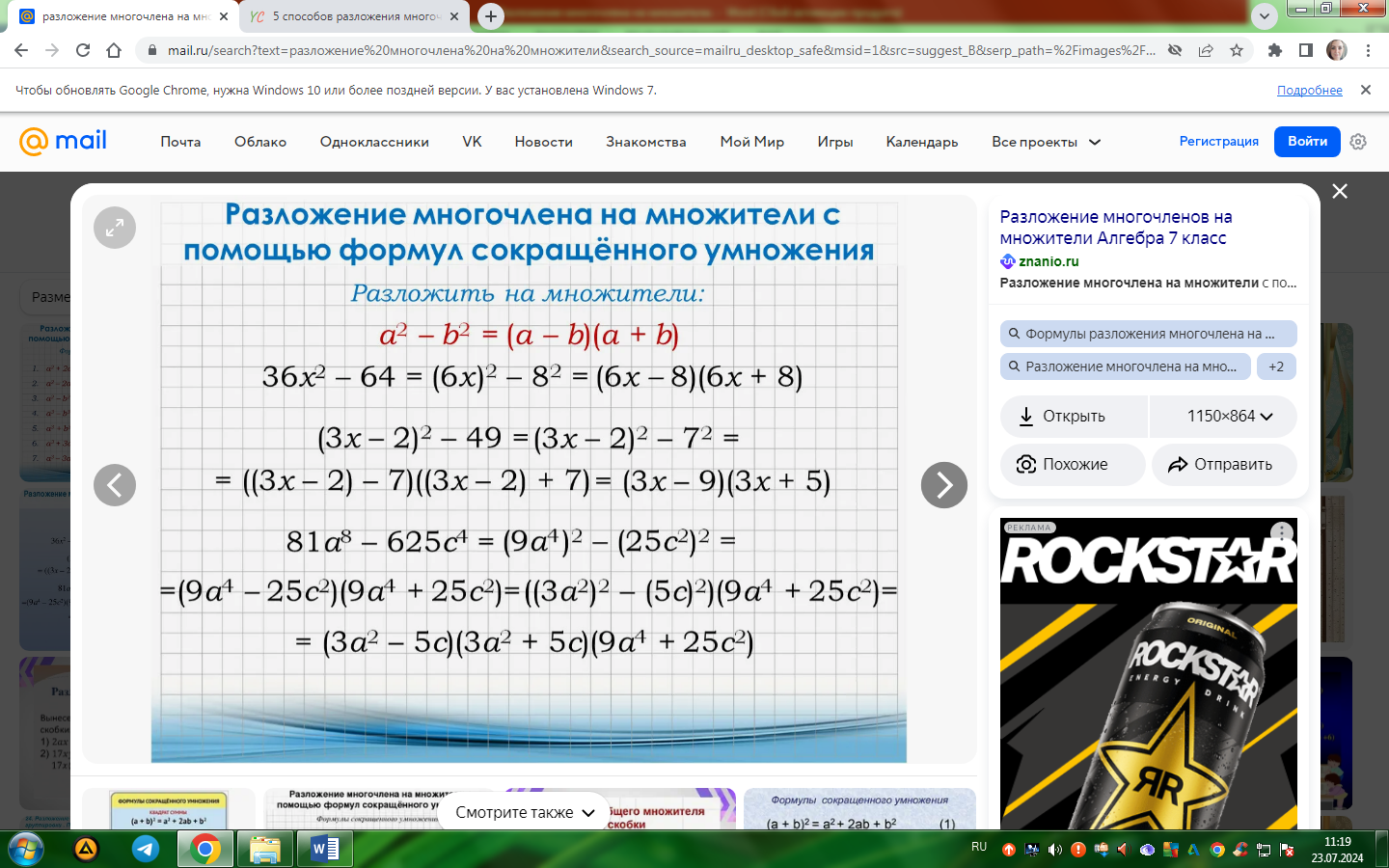
2. Формулы сокращенного умножения

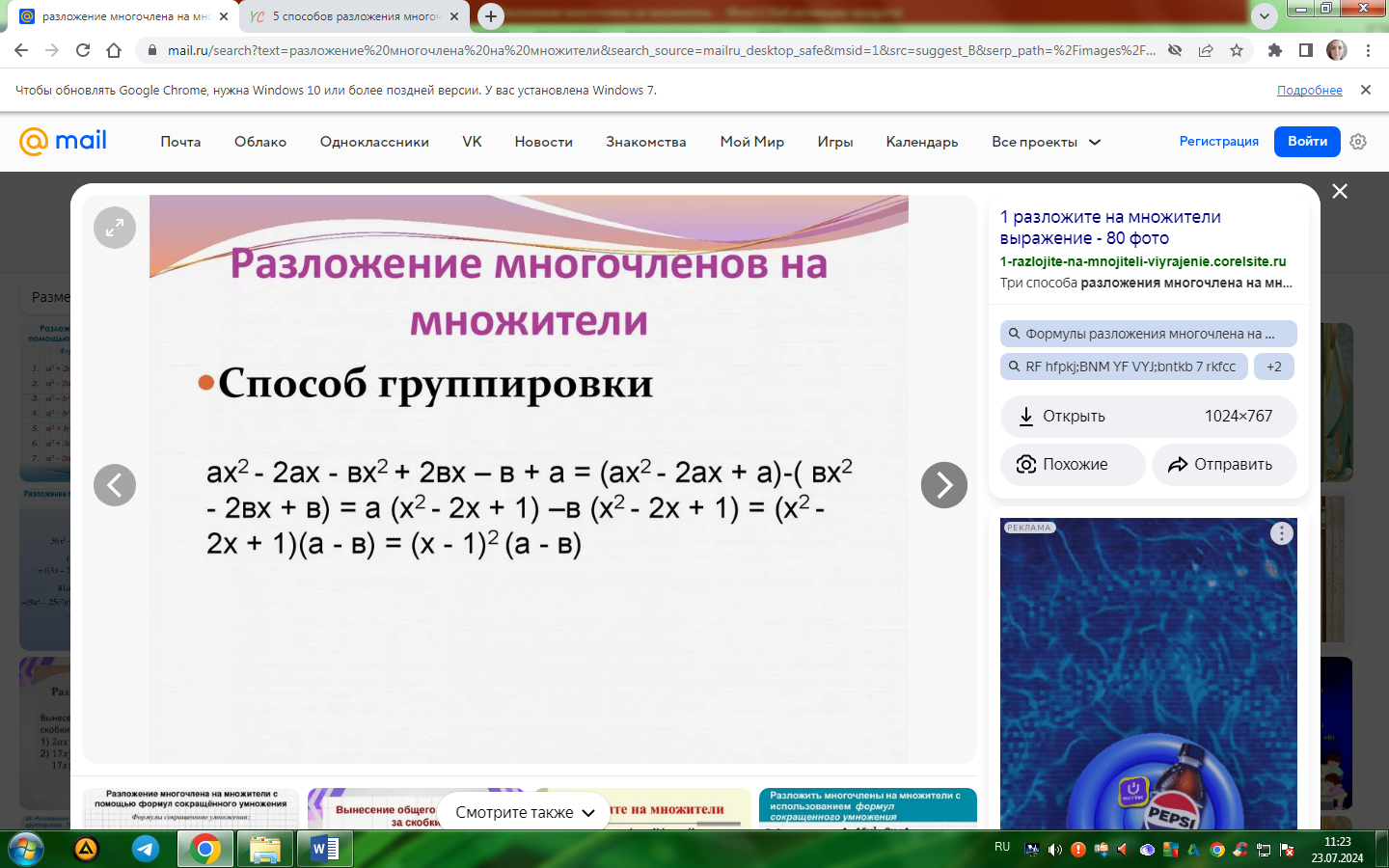
3. Метод группировки

Применяется если преобразование не очевидно.

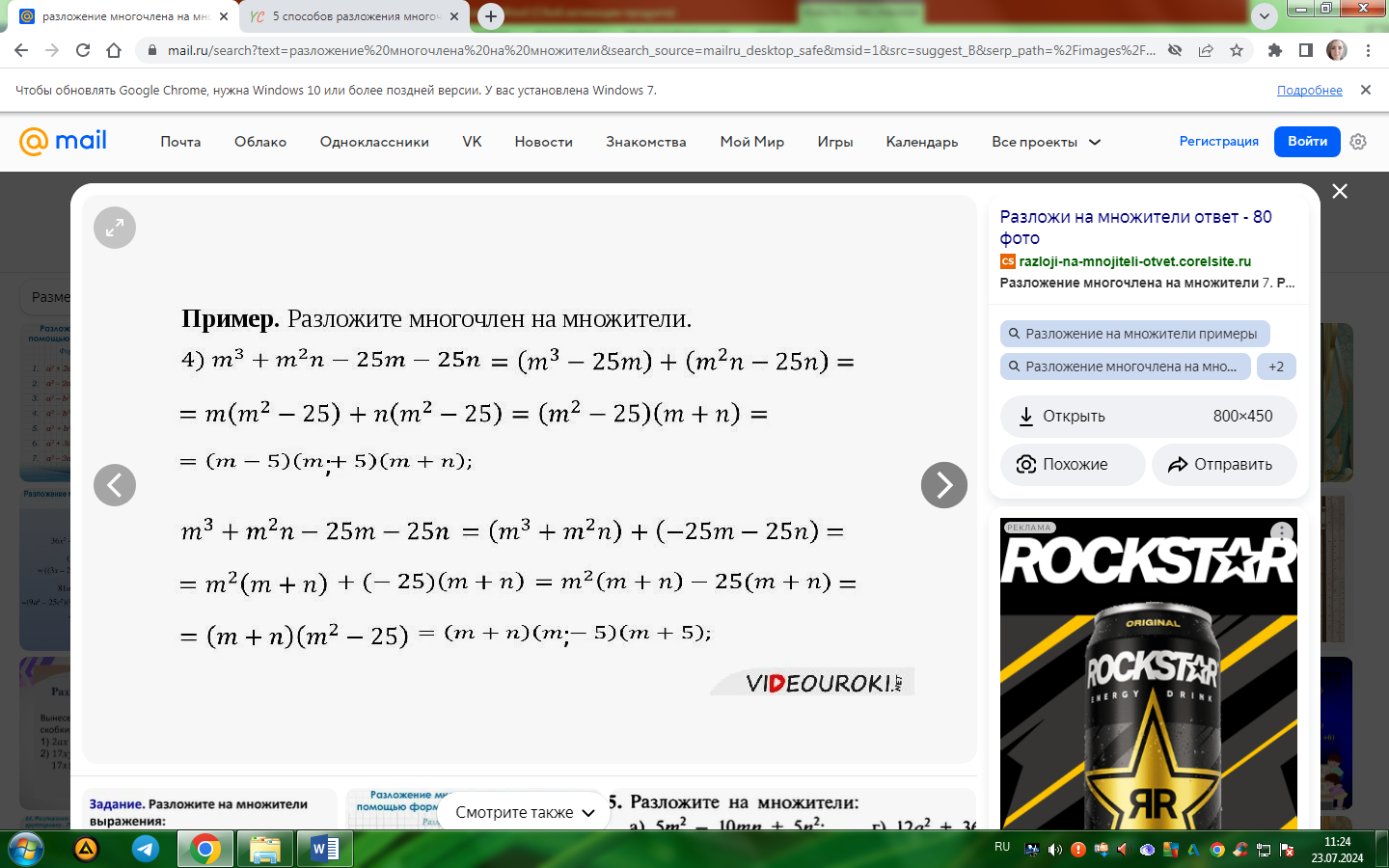
4. Разложение квадратного трехчлена на множители

5. Деление многочлена на линейный двучлен (х-а)

Многочлен делится на (х-а) тогда и только тогда, когда его значение при х=а равно 0, т.е. а при атом является корнем многочлена.

Если многочлен имеет целые или рациональные корни, то они обязательно являются делителями его свободного члена.