© 2024 302 3


СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока

8-nji synp algebra 3-nji çärýek sapak ýazgy
8-nji synp algebra 3-nji çärýek sapak ýazgy
Просмотр содержимого документа
«8-nji synp algebra 3-nji çärýek sapak ýazgy»
Mekdebi№: 4 Dersiň ady: Algebra
| Synpy: | VIII A | VIII B |
| Senesi: | | |
| Sapagyň temasy: | Kwadrat deňlemäniň kökleriniň formulasy |
| Sapagyň maksatlary: | |
| 1)Bilim berijilik maksady: | Kwadrat deňlemäniň kökleriniň formulasyny öwretmek. Okuwçylaryň öňki öwrenenlerini berkitmek, olaryň başarnyklaryny, ukyplaryny ösdürmek. |
| 2) Terbiýeçilik maksady: | Okuwçylary watançylyk, zähmetsöýerlik, beýik adamkärçilik ruhunda terbiýelemek. Olaryň watansöýüjilik duýgularyny ösdürmek. |
| Sapagyň görnüşi: | Täze maglumatlary öwretmek sapagy. |
| Sapakda ulanylýan okuw-görkezme esbaplar, sanly serişdeler, paýlama maglumatlar: | Kompýuter, interaktiw tagta, slaýdlar, tanyşdyrmalar, tablisalar, tema degişli soraglar, çyzgyç. |
Sapagyň gidişi:
1. Sapagyň guramaçylyk döwri:
1. Salamlaşmak. Gatnaşygy hasaba almak.
2. Okuwçylaryň ünsüni sapaga gönükdirmek.
3. Syýasy wakalar bilen tanyşdyrmak.
4. Gahryman Arkadagymyzyň «Paýhas çesmesi» «Paýhas çesmesi» kitabyndan sorag-jogap alyşmak.
2. Öý işiniň ýerine ýetirilişini barlamak:
358. 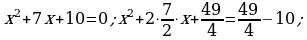
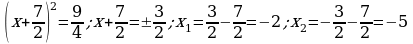 ;
;
3. Geçilen temany jemlemek:
Ikiagzanyň kwadratyny bölüp çykarmak bilen kwadrat deňlemäniň çözülişi
4. Täze temany düşündirmek:
Temany düşündirmegiň meýilnamasy:
1. Ikagzanyň kwadratyny bölüp çykarmak usuly barada umumy düşünje bermek.
2. Kwadrat deňlemeleriň köklerini tapmagy öwretmek
3. Kwadrat deňlemeleriň kökleriniň formulasyny öwretmek
Temany öwrenmek bilen okuwçylar bilmeli:
1. Ikagzanyň kwadratyny bölüp çykarmak usuly barada umumy düşünjelri bilmeli
2. Kwadrat deňlemeleriň kökleriniň formulasyny bilmeli
3. Kwadrat deňlemeleriň kökleriniň formulasyny bilmeli
Temany öwrenmek bilen okuwçylar başarmaly:
1. Ikagzanyň kwadratyny bölüp çykarmak usuly barada umumy düşünjeleri bilmekligi başarmaly.
2. Kwadrat deňlemeleriň köklerini tapmagy başarmaly
3. Kwadrat deňlemeleriň kökleriniň formulasyny getirip çykarmagy başarmaly
Biz ax2 + bx + c = 0 görnüşdäki deňlemäni ikagzanyň kwadratyny bölüp çykarmak usuly bilen çözmegi öwrendik. Ýöne bu usul käbir halda köp özgertmeleriň ýerine ýetirilmegini talap edýär. Şoňa görä-de, kwadrat deňlemäniň umumy görnüşini çözüp, onuň kökleriniň formulasyny çykarmak amatlydyr. Ol formulany islendik kwadrat deňlemäni çözmek üçin hem ulanyp bolýar.
Teorema. ax2 + bx + c = 0 (bu ýerde a, b, c – käbir sanlar, a ≠ 0, x – näbelli ululyk) deňlemäniň kökleri üçin 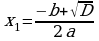 we
we 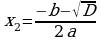 formulalar dogrudyr.
formulalar dogrudyr.
Ýatda saklaň! Diskriminantyň alamatyna baglylykda kwadrat deňlemäniň iki köki (D 0 bolanda), bir köki (D = 0 bolanda) bolup biler, D
ax2 + bx + c = 0 deňlemäni 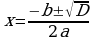 formulany ulanyp çözmek üçin:
formulany ulanyp çözmek üçin:
a) Ilki diskriminanty hasaplamaly we ony nol bilen deňeşdirmeli;
b) eger diskriminant položitel ýa-da nola deň bolsa, onda kökleriň formulasyndan peýdalanyp, deňlemäni çözmeli. Eger diskriminant otrisatel bolsa, onda deňlemäniň kökleri ýok diýip ýazmaly.
1-nji mysal. 6x2 + x – 2 = 0 deňlemäni çözmeli.
Bu deňlemede a = 6; b = 1; c = –2. Diskriminanty tapalyň.
D = b2 – 4ac = 12 – 4 ⋅ 6 ⋅ (–2) = 49 0.
Kwadrat deňlemäniň kökleriniň formulasyny ulanalyň.
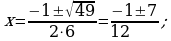
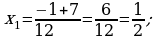
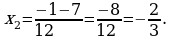
Jogaby: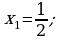
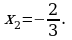
5. Täze temany berkitmek:
362. b)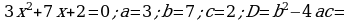
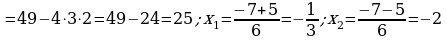
d) 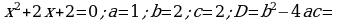
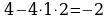 deňlemäniň köki ýok.
deňlemäniň köki ýok.
363. d)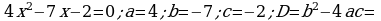
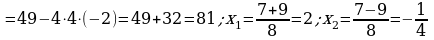 ;
;
6. Öý işini tabşyrmak:
Mysal N 364. b)
7. Sapagy jemlemek we okuwçylaryň bilimlerini bahalandyrmak:
Sapaga işjeň gatnaşan okuwçylary bahalandyrmak.
Ýazan mugallym: M.Işankulyýew
Bellik:_______________________________________________________________
Barlan: Müdiriň okuw işleri baradaky orunbasary ____________________________
Mekdebi№: 4 Dersiň ady: Algebra
| Synpy: | VIII A | VIII B |
| Senesi: | | |
| Sapagyň temasy: | Gönükme çözmek. |
| Sapagyň maksatlary: | |
| 1)Bilim berijilik maksady: | Kwadrat deňlemäniň kökleriniň formulasyny öwretmek. Okuwçylaryň öňki öwrenenlerini berkitmek, olaryň başarnyklaryny, ukyplaryny ösdürmek. |
| 2) Terbiýeçilik maksady: | Okuwçylary watançylyk, zähmetsöýerlik, beýik adamkärçilik ruhunda terbiýelemek. Olaryň watansöýüjilik duýgularyny ösdürmek. |
| Sapagyň görnüşi: | Täze maglumatlary öwretmek sapagy. |
| Sapakda ulanylýan okuw-görkezme esbaplar, sanly serişdeler, paýlama maglumatlar: | Kompýuter, interaktiw tagta, slaýdlar, tanyşdyrmalar, tablisalar, tema degişli soraglar, çyzgyç. |
Sapagyň gidişi:
1. Sapagyň guramaçylyk döwri:
1. Salamlaşmak. Gatnaşygy hasaba almak.
2. Okuwçylaryň ünsüni sapaga gönükdirmek.
3. Syýasy wakalar bilen tanyşdyrmak.
4. Gahryman Arkadagymyzyň «Paýhas çesmesi» «Paýhas çesmesi» kitabyndan sorag-jogap alyşmak.
2. Öý işiniň ýerine ýetirilişini barlamak:
364. b)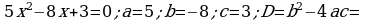
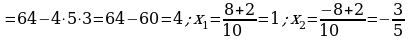 ;
;
3. Geçilen temany jemlemek:
Kwadrat deňlemäniň kökleriniň formulasy
4. Täze temany düşündirmek:
Temany düşündirmegiň meýilnamasy:
1. Ikagzanyň kwadratyny bölüp çykarmak usuly barada umumy düşünje bermek.
2. Kwadrat deňlemeleriň köklerini tapmagy öwretmek
3. Kwadrat deňlemeleriň kökleriniň formulasyny öwretmek
Temany öwrenmek bilen okuwçylar bilmeli:
1. Ikagzanyň kwadratyny bölüp çykarmak usuly barada umumy düşünjelri bilmeli
2. Kwadrat deňlemeleriň kökleriniň formulasyny bilmeli
3. Kwadrat deňlemeleriň kökleriniň formulasyny bilmeli
Temany öwrenmek bilen okuwçylar başarmaly:
1. Ikagzanyň kwadratyny bölüp çykarmak usuly barada umumy düşünjeleri bilmekligi başarmaly.
2. Kwadrat deňlemeleriň köklerini tapmagy başarmaly
3. Kwadrat deňlemeleriň kökleriniň formulasyny getirip çykarmagy başarmaly
Teorema. ax2 + bx + c = 0 (bu ýerde a, b, c – käbir sanlar, a ≠ 0, x – näbelli ululyk) deňlemäniň kökleri üçin 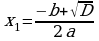 we
we 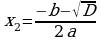 formulalar dogrudyr.
formulalar dogrudyr.
Ýatda saklaň! Diskriminantyň alamatyna baglylykda kwadrat deňlemäniň iki köki (D 0 bolanda), bir köki (D = 0 bolanda) bolup biler, D
ax2 + bx + c = 0 deňlemäni 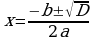 formulany ulanyp çözmek üçin:
formulany ulanyp çözmek üçin:
a) Ilki diskriminanty hasaplamaly we ony nol bilen deňeşdirmeli;
b) eger diskriminant položitel ýa-da nola deň bolsa, onda kökleriň formulasyndan peýdalanyp, deňlemäni çözmeli. Eger diskriminant otrisatel bolsa, onda deňlemäniň kökleri ýok diýip ýazmaly.
364. ä)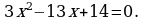
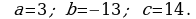
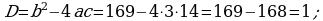
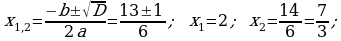
5. Täze temany berkitmek:
365. b) 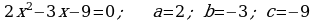
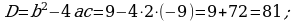
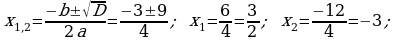
d) 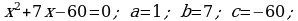
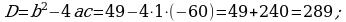
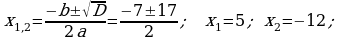
366. a) 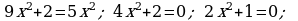
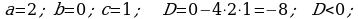
Jogaby: Deňlemäniň köki ýok.
6. Öý işini tabşyrmak:
Mysal N 366. d)
7. Sapagy jemlemek we okuwçylaryň bilimlerini bahalandyrmak:
Sapaga işjeň gatnaşan okuwçylary bahalandyrmak.
Ýazan mugallym: M.Işankulyýew
Bellik:_______________________________________________________________
Barlan: Müdiriň okuw işleri baradaky orunbasary ____________________________
Mekdebi№: 4 Dersiň ady: Algebra
| Synpy: | VIII A | VIII B |
| Senesi: | | |
| Sapagyň temasy: | Gönükme çözmek. |
| Sapagyň maksatlary: | |
| 1)Bilim berijilik maksady: | Kwadrat deňlemäniň kökleriniň formulasyny öwretmek. Okuwçylaryň öňki öwrenenlerini berkitmek, olaryň başarnyklaryny, ukyplaryny ösdürmek. |
| 2) Terbiýeçilik maksady: | Okuwçylary watançylyk, zähmetsöýerlik, beýik adamkärçilik ruhunda terbiýelemek. Olaryň watansöýüjilik duýgularyny ösdürmek. |
| Sapagyň görnüşi: | Täze maglumatlary öwretmek sapagy. |
| Sapakda ulanylýan okuw-görkezme esbaplar, sanly serişdeler, paýlama maglumatlar: | Kompýuter, interaktiw tagta, slaýdlar, tanyşdyrmalar, tablisalar, tema degişli soraglar, çyzgyç. |
Sapagyň gidişi:
1. Sapagyň guramaçylyk döwri:
1. Salamlaşmak. Gatnaşygy hasaba almak.
2. Okuwçylaryň ünsüni sapaga gönükdirmek.
3. Syýasy wakalar bilen tanyşdyrmak.
4. Gahryman Arkadagymyzyň «Paýhas çesmesi» «Paýhas çesmesi» kitabyndan sorag-jogap alyşmak.
2. Öý işiniň ýerine ýetirilişini barlamak:
366. d) 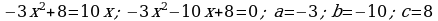
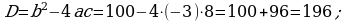
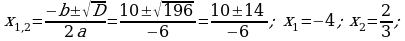
3. Geçilen temany jemlemek:
Kwadrat deňlemäniň kökleriniň formulasy
4. Täze temany düşündirmek:
Temany düşündirmegiň meýilnamasy:
1. Ikagzanyň kwadratyny bölüp çykarmak usuly barada umumy düşünje bermek.
2. Kwadrat deňlemeleriň köklerini tapmagy öwretmek
3. Kwadrat deňlemeleriň kökleriniň formulasyny öwretmek
Temany öwrenmek bilen okuwçylar bilmeli:
1. Ikagzanyň kwadratyny bölüp çykarmak usuly barada umumy düşünjelri bilmeli
2. Kwadrat deňlemeleriň kökleriniň formulasyny bilmeli
3. Kwadrat deňlemeleriň kökleriniň formulasyny bilmeli
Temany öwrenmek bilen okuwçylar başarmaly:
1. Ikagzanyň kwadratyny bölüp çykarmak usuly barada umumy düşünjeleri bilmekligi başarmaly.
2. Kwadrat deňlemeleriň köklerini tapmagy başarmaly
3. Kwadrat deňlemeleriň kökleriniň formulasyny getirip çykarmagy başarmaly
Teorema. ax2 + bx + c = 0 (bu ýerde a, b, c – käbir sanlar, a ≠ 0, x – näbelli ululyk) deňlemäniň kökleri üçin 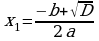 we
we 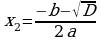 formulalar dogrudyr.
formulalar dogrudyr.
367. a) 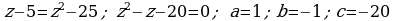 ;
;
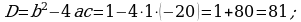
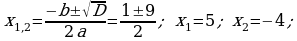
d) 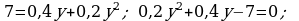
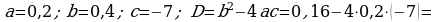
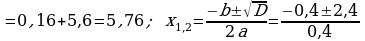
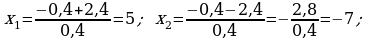
5. Täze temany berkitmek:
368. a)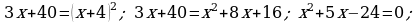
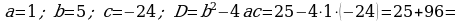
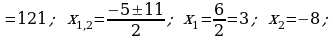
d) 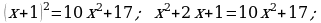
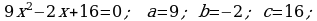
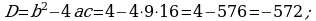
Jogaby: Kökleri ýok
6. Öý işini tabşyrmak:
Mysal N 370. b)
7. Sapagy jemlemek we okuwçylaryň bilimlerini bahalandyrmak:
Sapaga işjeň gatnaşan okuwçylary bahalandyrmak.
Ýazan mugallym: M.Işankulyýew
Bellik:_______________________________________________________________
Barlan: Müdiriň okuw işleri baradaky orunbasary ____________________________
Mekdebi№: 4 Dersiň ady: Algebra
| Synpy: | VIII A | VIII B |
| Senesi: | | |
| Sapagyň temasy: | Gönükme çözmek. |
| Sapagyň maksatlary: | |
| 1)Bilim berijilik maksady: | Kwadrat deňlemäniň kökleriniň formulasyny öwretmek. Okuwçylaryň öňki öwrenenlerini berkitmek, olaryň başarnyklaryny, ukyplaryny ösdürmek. |
| 2) Terbiýeçilik maksady: | Okuwçylary watançylyk, zähmetsöýerlik, beýik adamkärçilik ruhunda terbiýelemek. Olaryň watansöýüjilik duýgularyny ösdürmek. |
| Sapagyň görnüşi: | Täze maglumatlary öwretmek sapagy. |
| Sapakda ulanylýan okuw-görkezme esbaplar, sanly serişdeler, paýlama maglumatlar: | Kompýuter, interaktiw tagta, slaýdlar, tanyşdyrmalar, tablisalar, tema degişli soraglar, çyzgyç. |
Sapagyň gidişi:
1. Sapagyň guramaçylyk döwri:
1. Salamlaşmak. Gatnaşygy hasaba almak.
2. Okuwçylaryň ünsüni sapaga gönükdirmek.
3. Syýasy wakalar bilen tanyşdyrmak.
4. Gahryman Arkadagymyzyň «Paýhas çesmesi» «Paýhas çesmesi» kitabyndan sorag-jogap alyşmak.
2. Öý işiniň ýerine ýetirilişini barlamak:
370. b)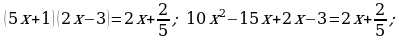
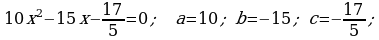
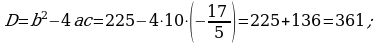
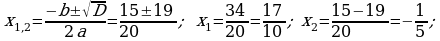
3. Geçilen temany jemlemek:
Kwadrat deňlemäniň kökleriniň formulasy
4. Täze temany düşündirmek:
Temany düşündirmegiň meýilnamasy:
1. Ikagzanyň kwadratyny bölüp çykarmak usuly barada umumy düşünje bermek.
2. Kwadrat deňlemeleriň köklerini tapmagy öwretmek
3. Kwadrat deňlemeleriň kökleriniň formulasyny öwretmek
Temany öwrenmek bilen okuwçylar bilmeli:
1. Ikagzanyň kwadratyny bölüp çykarmak usuly barada umumy düşünjelri bilmeli
2. Kwadrat deňlemeleriň kökleriniň formulasyny bilmeli
3. Kwadrat deňlemeleriň kökleriniň formulasyny bilmeli
Temany öwrenmek bilen okuwçylar başarmaly:
1. Ikagzanyň kwadratyny bölüp çykarmak usuly barada umumy düşünjeleri bilmekligi başarmaly.
2. Kwadrat deňlemeleriň köklerini tapmagy başarmaly
3. Kwadrat deňlemeleriň kökleriniň formulasyny getirip çykarmagy başarmaly
Teorema. ax2 + bx + c = 0 (bu ýerde a, b, c – käbir sanlar, a ≠ 0, x – näbelli ululyk) deňlemäniň kökleri üçin 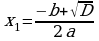 we
we 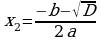 formulalar dogrudyr.
formulalar dogrudyr.
371. ç) 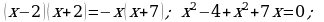

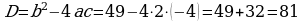
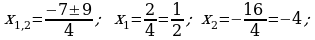
372. ç) 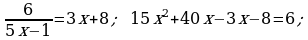
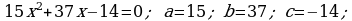
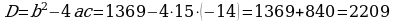
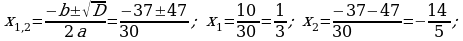
5. Täze temany berkitmek:
373. ç) 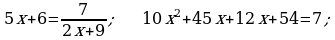
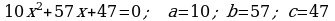
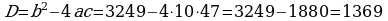
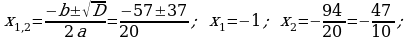
6. Öý işini tabşyrmak:
Mysal N 374. b)
7. Sapagy jemlemek we okuwçylaryň bilimlerini bahalandyrmak:
Sapaga işjeň gatnaşan okuwçylary bahalandyrmak.
Ýazan mugallym: M.Işankulyýew
Bellik:_______________________________________________________________
Barlan: Müdiriň okuw işleri baradaky orunbasary ____________________________
Mekdebi№: 4 Dersiň ady: Algebra
| Synpy: | VIII A | VIII B |
| Senesi: | | |
| Sapagyň temasy: | 4-nji ýazuw- barlag işi |
| Sapagyň maksady. | |
| 1) Bilim berijilik maksady: | Okuwçylaryň bilimini barlamak, pikirleniş endiklerini ösdürmek |
| 2) Terbiýeçilik maksady: | Okuwçylary watançylyk, zähmetsöýerlik, beýik adamkärçilik ruhunda terbiýelemek. Olaryň watansöýüjilik duýgularyny ösdürmek. |
| Sapagyň görnüşi: | Ýazuw-barlag işi geçirilýän sapak |
| Sapakda ulanylýan okuw-görkezme esbaplar, sanly serişdeler, paýlama maglumatlar: | Barlag iş depderleri |
Sapagyň gidişi:
1. Sapagyň guramaçylyk döwri:
1. Salamlaşmak. Gatnaşygy hasaba almak. 2. Okuwçylaryň sapaga taýýarlygyny barlamak.
3. Okuwçylaryň ünsüni sapaga gönükdirmek. 4. Syýasy wakalar bilen tanyşdyrmak.
2. Ýazuw-barlag işiniň mazmunyny düşündirmek.
Çep tarap
1) Deňlemäni çözüň:
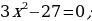
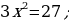
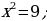
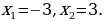
2) Deňlemäni 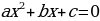 görnüşe getiriň.
görnüşe getiriň.
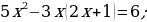
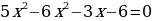
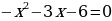
3) Kwadrat deňlemäniň kökleriniň formulasyny ulanyp deňlemäni çözüň.
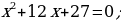
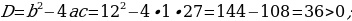
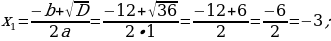
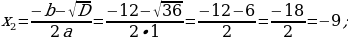
Sag tarap
1) Deňlemäni çözüň:
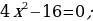
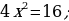
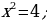
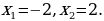
2) Deňlemäni 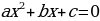 görnüşe getiriň.
görnüşe getiriň.
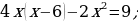
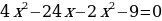
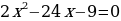
3) Kwadrat deňlemäniň kökleriniň formulasyny ulanyp deňlemäni çözüň.
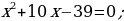
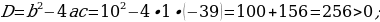
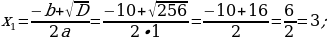
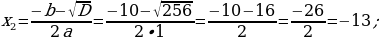
3. Okuwçylar tarapyndan ýazuw-barlag işiniň ýerine ýetirilmegi.
4. Sapagy jemlemek, öý işini tabşyrmak.
Okuwçylaryň depderlerini toplap almak. Sapagy umumylaşdyryp jemlemek.
Ýazan mugallym: M.Işankulyýew_
Bellik:________________________________________________________________
Barlan: Müdiriň okuw işleri baradaky orunbasary ____________________________
Mekdebi№: 4 Dersiň ady: Algebra
| Synpy: | VIII A | VIII B |
| Senesi: | | |
| Sapagyň temasy: | Wiýetiň teoremasy |
| Sapagyň maksatlary: | |
| 1)Bilim berijilik maksady: | Wiýetiň teoremasyny öwretmek. Okuwçylaryň öňki öwrenenlerini berkitmek, olaryň başarnyklaryny, ukyplaryny ösdürmek. |
| 2) Terbiýeçilik maksady: | Okuwçylary watançylyk, zähmetsöýerlik, beýik adamkärçilik ruhunda terbiýelemek. Olaryň watansöýüjilik duýgularyny ösdürmek. |
| Sapagyň görnüşi: | Täze maglumatlary öwretmek sapagy. |
| Sapakda ulanylýan okuw-görkezme esbaplar, sanly serişdeler, paýlama maglumatlar: | Kompýuter, interaktiw tagta, slaýdlar, tanyşdyrmalar, tablisalar, tema degişli soraglar, çyzgyç. |
Sapagyň gidişi:
1. Sapagyň guramaçylyk döwri:
1. Salamlaşmak. Gatnaşygy hasaba almak.
2. Okuwçylaryň ünsüni sapaga gönükdirmek.
3. Syýasy wakalar bilen tanyşdyrmak.
4. Gahryman Arkadagymyzyň «Paýhas çesmesi» «Paýhas çesmesi» kitabyndan sorag-jogap alyşmak.
2. Öý işiniň ýerine ýetirilişini barlamak:
4-nji ýazuw- barlag işi
3. Geçilen temany jemlemek:
Kwadrat deňlemäniň kökleriniň formulasy
4. Täze temany düşündirmek:
Temany düşündirmegiň meýilnamasy:
1. Ikagzanyň kwadratyny bölüp çykarmak usuly barada umumy düşünje bermek.
2. Kwadrat deňlemeleriň köklerini tapmagy öwretmek
3. Wiýetiň teoremasyny öwretmek
Temany öwrenmek bilen okuwçylar bilmeli:
1. Ikagzanyň kwadratyny bölüp çykarmak usuly barada umumy düşünjelri bilmeli
2. Kwadrat deňlemeleriň kökleriniň formulasyny bilmeli
3. Wiýetiň teoremasyny bilmeli
Temany öwrenmek bilen okuwçylar başarmaly:
1. Ikagzanyň kwadratyny bölüp çykarmak usuly barada umumy düşünjeleri bilmekligi başarmaly.
2. Kwadrat deňlemeleriň köklerini tapmagy başarmaly
3. Wiýetiň teoremasyny subut etmegi başarmaly
x2 – 7x + 12 = 0
getirilen kwadrat deňlemäniň x1= 3 we x2 = 4 kökleri bar. Bu kökleriň jemi 7-ä deň:
x1 + x2 = 7, köpeltmek hasyly bolsa 12-ä deň:
x1 · x2 = 3 · 4 = 12.
Getirilen kwadrat deňlemede kökleriniň jeminiň garşylykly alamaty bilen alnany, ikinji agzanyň koeffisiýentine, kökleriniň köpeltmek hasyly bolsa azat agza deňdigini görýäris. Getirilen
kwadrat deňlemäniň ikinji agzasynyň koeffisiýenti we azat agzasy bilen onuň kökleriniň arasyndaky baglanyşygy baradaky teoremany ilkinji gezek fransuz matematigi Fransua Wiýet subut etdi. Şoňa görä-de, bu teorema onuň hormatyna «Wiýetiň teoremasy» diýlip atlandyrylýar.
Fransua Wiýet (1540–1603) fransuz matematigi, elementar algebranyň esasyny işläp düzdi. Ol sanlary harplar bilen belgilänleriň ilkinjileriniň biridir. Bu bolsa deňlemeler nazaryýetiniň düýpli ösmegine ýardam etdi.
Wiýetiň teoremasy. Eger x2 + px + q = 0 (bu ýerde p, q – käbir sanlar, x – näbelli ululyk) getirilen kwadrat deňlemäniň x1 we x2 kökleri bar bolsa, onda x1 + x2 = – p
we x1 · x2 = q deňlikler dogrudyr.
Wiýetiň teoremasyndan peýdalanyp islendik kwadrat deňlemäniň kökleriniň jemini we köpeltmek hasylyny onuň koeffi-siýentleri arkaly aňladyp bolýar.
Eger ax2 + bx + c = 0 deňlemäniň x1 we x2 kökleri bar bolsa, onda 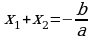 we
we 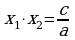 deňlikler ýerine ýetýär. Wiýetiň teoremasyna ters bolan tassyklama hem dogrudyr.
deňlikler ýerine ýetýär. Wiýetiň teoremasyna ters bolan tassyklama hem dogrudyr.
Ters teorema: Eger x1 we x2 sanlaryň jemi (–p), olaryň köpeltmek hasyly q deň bolsa, onda ol sanlar x2+px+q=0 deňlemäniň kökleridir.
Şeýlelikde, x näbelliniň x1 bahasy berlen deňlemäni toždestwo öwürýär. Diýmek, x1 san x2 + px + q = 0 deňlemäniň köki.
x = x2 sanyň hem x2 + px + q = 0 deňlemäniň köki bolýandygy şuňa meňzeş subut edilýär.
1-nji mysal. 2x2 + 5x + 2 = 0 deňlemäni çözmän, onuň kökleriniň jemini we köpeltmek hasylyny tapalyň.
D = 52 – 4 · 2 · 2 = 9 0 bolýandygyna görä berlen deňlemäniň iki köki bardyr. Berlen deňlemäniň iki bölegini-de birinji agzanyň koeffisiýentine bölüp, oňa deňgüýçli bolan
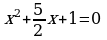 getirilen kwadrat deňlemäni alarys. Wiýetiň teoremasyna görä:
getirilen kwadrat deňlemäni alarys. Wiýetiň teoremasyna görä:
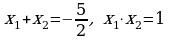
5. Täze temany berkitmek:
411. 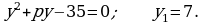
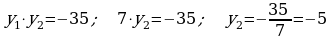
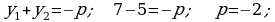
413. 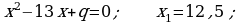
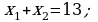
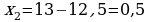 ;
;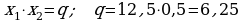
6. Öý işini tabşyrmak:
1. Getirilen kwadrat deňlemäniň ikinji koeffisiýenti we azat agzasy bilen onuň kökleriniň arasynda nähili baglanyşyk bar?
2. ax2 + bx + c = 0 deňleme üçin Wiýetiň teoremasy nähili aňladylýar? 3. Wiýetiň teoremasyna ters bolan teoremany aýdyň.
4. Kwadrat deňlemäni çözmän, onuň kökleriniň jemini we köpeltmek
hasylyny tapyp bolarmy?
5. Kwadrat deňlemäni çözmän, onuň bitin köklerini nähili tapmaly?
6. Kökleri berlen sanlar bolan getirilen kwadrat deňleme nähili ýazylýar?
7. Sapagy jemlemek we okuwçylaryň bilimlerini bahalandyrmak:
Sapaga işjeň gatnaşan okuwçylary bahalandyrmak.
Ýazan mugallym: M.Işankulyýew
Bellik:_______________________________________________________________
Barlan: Müdiriň okuw işleri baradaky orunbasary ____________________________
Mekdebi№: 4 Dersiň ady: Algebra
| Synpy: | VIII A | VIII B |
| Senesi: | | |
| Sapagyň temasy: | Gönükme çözmek. |
| Sapagyň maksatlary: | |
| 1)Bilim berijilik maksady: | Wiýetiň teoremasyny öwretmek. Okuwçylaryň öňki öwrenenlerini berkitmek, olaryň başarnyklaryny, ukyplaryny ösdürmek. |
| 2) Terbiýeçilik maksady: | Okuwçylary watançylyk, zähmetsöýerlik, beýik adamkärçilik ruhunda terbiýelemek. Olaryň watansöýüjilik duýgularyny ösdürmek. |
| Sapagyň görnüşi: | Täze maglumatlary öwretmek sapagy. |
| Sapakda ulanylýan okuw-görkezme esbaplar, sanly serişdeler, paýlama maglumatlar: | Kompýuter, interaktiw tagta, slaýdlar, tanyşdyrmalar, tablisalar, tema degişli soraglar, çyzgyç. |
Sapagyň gidişi:
1. Sapagyň guramaçylyk döwri:
1. Salamlaşmak. Gatnaşygy hasaba almak.
2. Okuwçylaryň ünsüni sapaga gönükdirmek.
3. Syýasy wakalar bilen tanyşdyrmak.
4. Gahryman Arkadagymyzyň «Paýhas çesmesi» «Paýhas çesmesi» kitabyndan sorag-jogap alyşmak.
2. Öý işiniň ýerine ýetirilişini barlamak:
1. Getirilen kwadrat deňlemäniň ikinji koeffisiýenti we azat agzasy bilen onuň kökleriniň arasynda nähili baglanyşyk bar?
2. ax2 + bx + c = 0 deňleme üçin Wiýetiň teoremasy nähili aňladylýar? 3. Wiýetiň teoremasyna ters bolan teoremany aýdyň.
4. Kwadrat deňlemäni çözmän, onuň kökleriniň jemini we köpeltmek
hasylyny tapyp bolarmy?
5. Kwadrat deňlemäni çözmän, onuň bitin köklerini nähili tapmaly?
6. Kökleri berlen sanlar bolan getirilen kwadrat deňleme nähili ýazylýar?
3. Geçilen temany jemlemek:
Wiýetiň teoremasy
4. Täze temany düşündirmek:
Temany düşündirmegiň meýilnamasy:
1. Ikagzanyň kwadratyny bölüp çykarmak usuly barada umumy düşünje bermek.
2. Kwadrat deňlemeleriň köklerini tapmagy öwretmek
3. Wiýetiň teoremasyny öwretmek
Temany öwrenmek bilen okuwçylar bilmeli:
1. Ikagzanyň kwadratyny bölüp çykarmak usuly barada umumy düşünjelri bilmeli
2. Kwadrat deňlemeleriň kökleriniň formulasyny bilmeli
3. Wiýetiň teoremasyny bilmeli
Temany öwrenmek bilen okuwçylar başarmaly:
1. Ikagzanyň kwadratyny bölüp çykarmak usuly barada umumy düşünjeleri bilmekligi başarmaly.
2. Kwadrat deňlemeleriň köklerini tapmagy başarmaly
3. Wiýetiň teoremasyny subut etmegi başarmaly
Wiýetiň teoremasy. Eger x2 + px + q = 0 (bu ýerde p, q – käbir sanlar, x – näbelli ululyk) getirilen kwadrat deňlemäniň x1 we x2 kökleri bar bolsa, onda x1 + x2 = – p
we x1 · x2 = q deňlikler dogrudyr.
Wiýetiň teoremasyndan peýdalanyp islendik kwadrat deňlemäniň kökleriniň jemini we köpeltmek hasylyny onuň koeffi-siýentleri arkaly aňladyp bolýar.
Eger ax2 + bx + c = 0 deňlemäniň x1 we x2 kökleri bar bolsa, onda 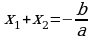 we
we 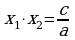 deňlikler ýerine ýetýär. Wiýetiň teoremasyna ters bolan tassyklama hem dogrudyr.
deňlikler ýerine ýetýär. Wiýetiň teoremasyna ters bolan tassyklama hem dogrudyr.
Ters teorema: Eger x1 we x2 sanlaryň jemi (–p), olaryň köpeltmek hasyly q deň bolsa, onda ol sanlar x2+px+q=0 deňlemäniň kökleridir.
Şeýlelikde, x näbelliniň x1 bahasy berlen deňlemäni toždestwo öwürýär. Diýmek, x1 san x2 + px + q = 0 deňlemäniň köki.
x = x2 sanyň hem x2 + px + q = 0 deňlemäniň köki bolýandygy şuňa meňzeş subut edilýär.
415. 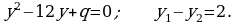
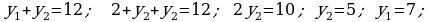
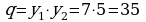
417. 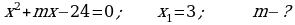
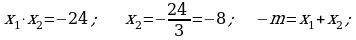
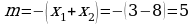
5. Täze temany berkitmek:
419. 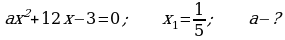
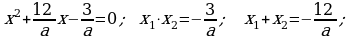
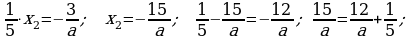
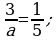
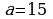 .
.
6. Öý işini tabşyrmak:
Mysal N 421 b).
7. Sapagy jemlemek we okuwçylaryň bilimlerini bahalandyrmak:
Sapaga işjeň gatnaşan okuwçylary bahalandyrmak.
Ýazan mugallym: M.Işankulyýew
Bellik:_______________________________________________________________
Barlan: Müdiriň okuw işleri baradaky orunbasary ____________________________
Mekdebi№:4 Dersiň ady: Algebra
| Synpy: | VIII A | VIII B |
| Senesi: | | |
| Sapagyň temasy: | Gönükme çözmek. |
| Sapagyň maksatlary: | |
| 1)Bilim berijilik maksady: | Wiýetiň teoremasyny öwretmek. Okuwçylaryň öňki öwrenenlerini berkitmek, olaryň başarnyklaryny, ukyplaryny ösdürmek. |
| 2) Terbiýeçilik maksady: | Okuwçylary watançylyk, zähmetsöýerlik, beýik adamkärçilik ruhunda terbiýelemek. Olaryň watansöýüjilik duýgularyny ösdürmek. |
| Sapagyň görnüşi: | Täze maglumatlary öwretmek sapagy. |
| Sapakda ulanylýan okuw-görkezme esbaplar, sanly serişdeler, paýlama maglumatlar: | Kompýuter, interaktiw tagta, slaýdlar, tanyşdyrmalar, tablisalar, tema degişli soraglar, çyzgyç. |
Sapagyň gidişi:
1. Sapagyň guramaçylyk döwri:
1. Salamlaşmak. Gatnaşygy hasaba almak.
2. Okuwçylaryň ünsüni sapaga gönükdirmek.
3. Syýasy wakalar bilen tanyşdyrmak.
4. Gahryman Arkadagymyzyň «Paýhas çesmesi» «Paýhas çesmesi» kitabyndan sorag-jogap alyşmak.
2. Öý işiniň ýerine ýetirilişini barlamak:
421. b) 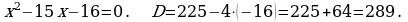
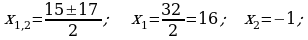
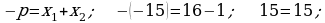
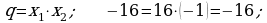
3. Geçilen temany jemlemek:
Wiýetiň teoremasy
4. Täze temany düşündirmek:
Temany düşündirmegiň meýilnamasy:
1. Ikagzanyň kwadratyny bölüp çykarmak usuly barada umumy düşünje bermek.
2. Kwadrat deňlemeleriň köklerini tapmagy öwretmek
3. Wiýetiň teoremasyny öwretmek
Temany öwrenmek bilen okuwçylar bilmeli:
1. Ikagzanyň kwadratyny bölüp çykarmak usuly barada umumy düşünjelri bilmeli
2. Kwadrat deňlemeleriň kökleriniň formulasyny bilmeli
3. Wiýetiň teoremasyny bilmeli
Temany öwrenmek bilen okuwçylar başarmaly:
1. Ikagzanyň kwadratyny bölüp çykarmak usuly barada umumy düşünjeleri bilmekligi başarmaly.
2. Kwadrat deňlemeleriň köklerini tapmagy başarmaly
3. Wiýetiň teoremasyny subut etmegi başarmaly
Wiýetiň teoremasy. Eger x2 + px + q = 0 (bu ýerde p, q – käbir sanlar, x – näbelli ululyk) getirilen kwadrat deňlemäniň x1 we x2 kökleri bar bolsa, onda x1 + x2 = – p
we x1 · x2 = q deňlikler dogrudyr.
Ters teorema: Eger x1 we x2 sanlaryň jemi (–p), olaryň köpeltmek hasyly q deň bolsa, onda ol sanlar x2+px+q=0 deňlemäniň kökleridir.
420-nji gönükme
Deňlemäni çözüň we çözülişiniň dogrudygyny Wiýetiň teoremasyna ters bolan teoremanyň esasynda barlaň.
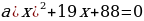
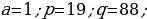
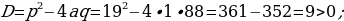
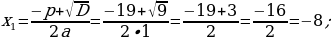
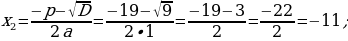
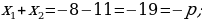
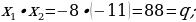
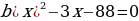
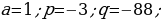
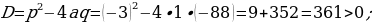
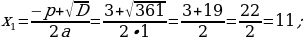
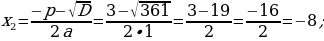
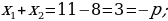
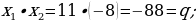
421 ä) 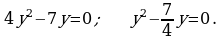
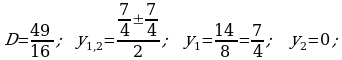
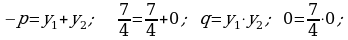
5. Täze temany berkitmek:
424. a) 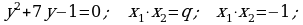
kökleriň biri otrisatel, biri bolsa položitel.
b) 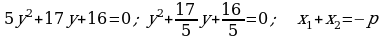
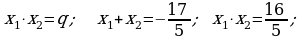 kökleriň ikisi hem otrisatel.
kökleriň ikisi hem otrisatel.
6. Öý işini tabşyrmak:
Mysal N 425. ç)
7. Sapagy jemlemek we okuwçylaryň bilimlerini bahalandyrmak:
Sapaga işjeň gatnaşan okuwçylary bahalandyrmak.
Ýazan mugallym: M.Işankulyýew
Bellik:_______________________________________________________________
Barlan: Müdiriň okuw işleri baradaky orunbasary ____________________________
Mekdebi№: 4 Dersiň ady: Algebra
| Synpy: | VIII A | VIII B |
| Senesi: | | |
| Sapagyň temasy: | Gönükme çözmek. |
| Sapagyň maksatlary: | |
| 1)Bilim berijilik maksady: | Wiýetiň teoremasyny öwretmek. Okuwçylaryň öňki öwrenenlerini berkitmek, olaryň başarnyklaryny, ukyplaryny ösdürmek. |
| 2) Terbiýeçilik maksady: | Okuwçylary watançylyk, zähmetsöýerlik, beýik adamkärçilik ruhunda terbiýelemek. Olaryň watansöýüjilik duýgularyny ösdürmek. |
| Sapagyň görnüşi: | Täze maglumatlary öwretmek sapagy. |
| Sapakda ulanylýan okuw-görkezme esbaplar, sanly serişdeler, paýlama maglumatlar: | Kompýuter, interaktiw tagta, slaýdlar, tanyşdyrmalar, tablisalar, tema degişli soraglar, çyzgyç. |
Sapagyň gidişi:
1. Sapagyň guramaçylyk döwri:
1. Salamlaşmak. Gatnaşygy hasaba almak.
2. Okuwçylaryň ünsüni sapaga gönükdirmek.
3. Syýasy wakalar bilen tanyşdyrmak.
4. Gahryman Arkadagymyzyň «Paýhas çesmesi» «Paýhas çesmesi» kitabyndan sorag-jogap alyşmak.
2. Öý işiniň ýerine ýetirilişini barlamak:
425. ç) 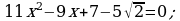
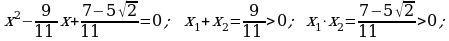
Kökleriň ikisi hem položitel
3. Geçilen temany jemlemek:
Wiýetiň teoremasy
4. Täze temany düşündirmek:
Temany düşündirmegiň meýilnamasy:
1. Ikagzanyň kwadratyny bölüp çykarmak usuly barada umumy düşünje bermek.
2. Kwadrat deňlemeleriň köklerini tapmagy öwretmek
3. Wiýetiň teoremasyny öwretmek
Temany öwrenmek bilen okuwçylar bilmeli:
1. Ikagzanyň kwadratyny bölüp çykarmak usuly barada umumy düşünjelri bilmeli
2. Kwadrat deňlemeleriň kökleriniň formulasyny bilmeli
3. Wiýetiň teoremasyny bilmeli
Temany öwrenmek bilen okuwçylar başarmaly:
1. Ikagzanyň kwadratyny bölüp çykarmak usuly barada umumy düşünjeleri bilmekligi başarmaly.
2. Kwadrat deňlemeleriň köklerini tapmagy başarmaly
3. Wiýetiň teoremasyny subut etmegi başarmaly
Wiýetiň teoremasy. Eger x2 + px + q = 0 (bu ýerde p, q – käbir sanlar, x – näbelli ululyk) getirilen kwadrat deňlemäniň x1 we x2 kökleri bar bolsa, onda x1 + x2 = – p
we x1 · x2 = q deňlikler dogrudyr.
Ters teorema: Eger x1 we x2 sanlaryň jemi (–p), olaryň köpeltmek hasyly q deň bolsa, onda ol sanlar x2+px+q=0 deňlemäniň kökleridir.
423. b) 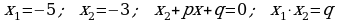
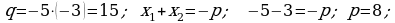
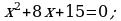
ç) 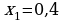 we
we 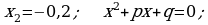
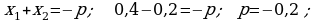
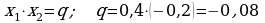 ;
; 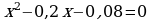 .
.
5. Täze temany berkitmek:
425 d) 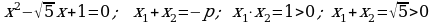
kökleriň ikisi hem položitel.
409-njy gönükme
Deňlemäni çözmezden, onuň kökleriniň jemini we köpeltmek hasylyny tapyň.
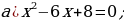
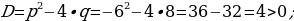
Wiýetiň teoremasyna görä
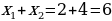 ;
;
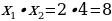
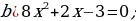
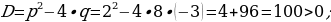
Wiýetiň teoremasyna görä
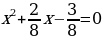
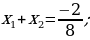
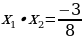
6. Öý işini tabşyrmak:
1. Getirilen kwadrat deňlemäniň ikinji koeffisiýenti we azat agzasy bilen onuň kökleriniň arasynda nähili baglanyşyk bar?
2. ax2 + bx + c = 0 deňleme üçin Wiýetiň teoremasy nähili aňladylýar? 3. Wiýetiň teoremasyna ters bolan teoremany aýdyň.
4. Kwadrat deňlemäni çözmän, onuň kökleriniň jemini we köpeltmek
hasylyny tapyp bolarmy?
5. Kwadrat deňlemäni çözmän, onuň bitin köklerini nähili tapmaly?
6. Kökleri berlen sanlar bolan getirilen kwadrat deňleme nähili ýazylýar?
7. Sapagy jemlemek we okuwçylaryň bilimlerini bahalandyrmak:
Höweslendiriji bahalary goýmak we delillendirmek Okuwçylary delillendirip bahalandyrmak.
Ýazan mugallym: M.Işankulyýew
Bellik:_______________________________________________________________
Barlan: Müdiriň okuw işleri baradaky orunbasary ____________________________
Mekdebi№: 4 Dersiň ady: Algebra
| Synpy: | VIII A | VIII B |
| Senesi: | | |
| Sapagyň temasy: | Kwadrat deňlemeleriň kömegi bilen meseleler çözmek |
| Sapagyň maksatlary: | |
| 1)Bilim berijilik maksady: | Kwadrat deňlemeleriň kömegi bilen meseleler çözmegi öwretmek. Okuwçylaryň öňki öwrenenlerini berkitmek, olaryň başarnyklaryny, ukyplaryny ösdürmek. |
| 2) Terbiýeçilik maksady: | Okuwçylary watançylyk, zähmetsöýerlik, beýik adamkärçilik ruhunda terbiýelemek. Olaryň watansöýüjilik duýgularyny ösdürmek. |
| Sapagyň görnüşi: | Täze maglumatlary öwretmek sapagy. |
| Sapakda ulanylýan okuw-görkezme esbaplar, sanly serişdeler, paýlama maglumatlar: | Kompýuter, interaktiw tagta, slaýdlar, tanyşdyrmalar, tablisalar, tema degişli soraglar, çyzgyç. |
Sapagyň gidişi:
1. Sapagyň guramaçylyk döwri:
1. Salamlaşmak. Gatnaşygy hasaba almak.
2. Okuwçylaryň ünsüni sapaga gönükdirmek.
3. Syýasy wakalar bilen tanyşdyrmak.
4. Gahryman Arkadagymyzyň «Paýhas çesmesi» «Paýhas çesmesi» kitabyndan sorag-jogap alyşmak.
2. Öý işiniň ýerine ýetirilişini barlamak:
1. Getirilen kwadrat deňlemäniň ikinji koeffisiýenti we azat agzasy bilen onuň kökleriniň arasynda nähili baglanyşyk bar?
2. ax2 + bx + c = 0 deňleme üçin Wiýetiň teoremasy nähili aňladylýar? 3. Wiýetiň teoremasyna ters bolan teoremany aýdyň.
4. Kwadrat deňlemäni çözmän, onuň kökleriniň jemini we köpeltmek
hasylyny tapyp bolarmy?
5. Kwadrat deňlemäni çözmän, onuň bitin köklerini nähili tapmaly?
6. Kökleri berlen sanlar bolan getirilen kwadrat deňleme nähili ýazylýar?
3. Geçilen temany jemlemek:
Wiýetiň teoremasy
4. Täze temany düşündirmek:
Temany düşündirmegiň meýilnamasy:
1.Kwadrat deňlemäniň kökleriniň formulasy barada umumy düşünje bermek.
2. Kwadrat deňlemeleriň köklerini tapmagy öwretmek
3. Kwadrat deňlemeleriň kömegi bilen meseleler çözmegi öwretmek
Temany öwrenmek bilen okuwçylar bilmeli:
1.Kwadrat deňlemäniň kökleriniň formulasy barada umumy düşünjeleri bilmeli.
2. Kwadrat deňlemeleriň köklerini tapmagy bilmeli
3. Kwadrat deňlemeleriň kömegi bilen meseleler çözmegi bilmeli
Temany öwrenmek bilen okuwçylar başarmaly:
1.Kwadrat deňlemäniň kökleriniň formulasy barada umumy düşünjeleri bilmegi başarmaly
2. Kwadrat deňlemeleriň köklerini tapmagy başarmaly
3. Kwadrat deňlemeleriň kömegi bilen meseleler çözmegi başarmaly
Matematikanyň, fizikanyň, tehnikanyň köp meseleleri kwadrat deňlemeleriň kömegi bilen çözülýär.
1-nji mysal. Bir tarapy beýlekisinden 5 m uly bolan gönüburçlugyň meýdany 84 m2 bolsa, onuň taraplaryny tapyň.
Çözülişi. Goý, gönüburçlugyň bir tarapy x m bolsun. Onda onuň beýleki tarapy (x + 5)m bolar. Şerte görä:
x(x + 5) = 84.
Alnan deňlemäni ýönekeýleşdireliň:
x2 + 5x – 84 = 0.
Bu deňlemäni çözüp, x1 = –12, x2 = 7 kökleri taparys. Meseläniň şertine görä, x položitel san bolmaly. Onda gönüburçlugyň bir tarapy 7m, beýleki tarapy bolsa 7 + 5 = 12 m bolar.
Jogaby: 7 m, 12 m.
2-nji mysal. Jisim 30 m/s başlangyç tizlik bilen dik ýokary zyňlypdyr. Ol näçe sekuntdan soň 40 m beýiklikde bolar?
Ç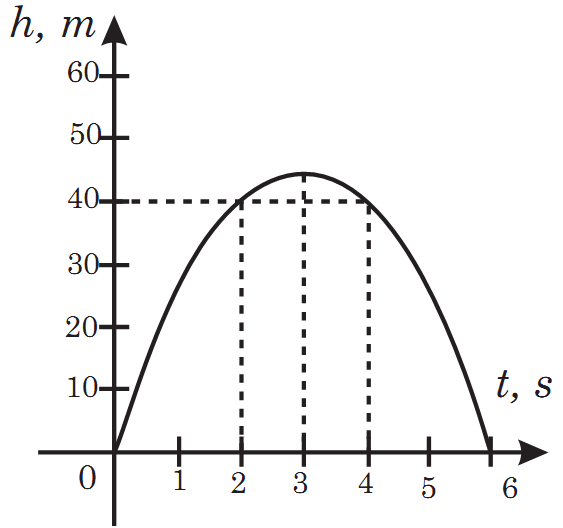 özülişi. Fizika dersinden belli bolşy ýaly, dik ýokaryk zyňlan jisimiň t sekuntdan soň galýan h beýikligi
özülişi. Fizika dersinden belli bolşy ýaly, dik ýokaryk zyňlan jisimiň t sekuntdan soň galýan h beýikligi
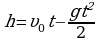
formula bilen tapylýar. Bu ýerde v0 – başlangyç tizlik (m/s), g – takmyny bahasy 10 m/s2-a deň bolan ýokardan erkin gaçma tizlenmesi.
Ýokardaky formulada h = 40 m, v0 = 30 m/s bahalary ornuna goýup alarys:
40 = 30t – 5t2.
Bu ýerden:
5t2 – 30t + 40 = 0,
t2 – 6t + 8 = 0.
Bu kwadrat deňlemäni çözüp t1 =2,
t2 = 4 bahalary tapýarys.
Tapylan kökleriň manysyna düşünmek üçin h = 30t – 5t2 baglylygyň grafigine seredeliň (8nji surat).
Grafikden görnüşi ýaly, zyňlan jisim ilkinji 3 sekundyň dowamynda
45 me çenli ýokaryk galýar, soňra bolsa ol aşaklap, 6 sekuntdan soň ýere düşýär.
Şeýlelikde, jisim zyňlandan 2 sekuntdan we 4 sekuntdan soňra ýerden 40 m beýiklige galar.
Jogaby: jisim zyňlandan 2 sekuntdan we 4 sekuntdan soňra
40 m beýiklikde bolar.
5. Täze temany berkitmek:
384. 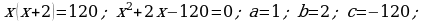
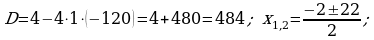
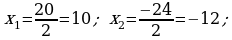 Jogaby: 10 we 12
Jogaby: 10 we 12
6. Öý işini tabşyrmak:
1. Näme üçin birinji meselede x-iň bahasy položitel bolmaly?
2. Ikinji meselede jisim ýerden 25 m beýiklikde näçe gezek bolýar?
7. Sapagy jemlemek we okuwçylaryň bilimlerini bahalandyrmak:
Höweslendiriji bahalary goýmak we delillendirmek Okuwçylary delillendirip bahalandyrmak.
Ýazan mugallym: M.Işankulyýew
Bellik:_______________________________________________________________
Barlan: Müdiriň okuw işleri baradaky orunbasary ____________________________
Mekdebi№: 4 Dersiň ady: Algebra
| Synpy: | VIII A | VIII B |
| Senesi: | | |
| Sapagyň temasy: | Gönükme çözmek. |
| Sapagyň maksatlary: | |
| 1)Bilim berijilik maksady: | Kwadrat deňlemeleriň kömegi bilen meseleler çözmegi öwretmek. Okuwçylaryň öňki öwrenenlerini berkitmek, olaryň başarnyklaryny, ukyplaryny ösdürmek. |
| 2) Terbiýeçilik maksady: | Okuwçylary watançylyk, zähmetsöýerlik, beýik adamkärçilik ruhunda terbiýelemek. Olaryň watansöýüjilik duýgularyny ösdürmek. |
| Sapagyň görnüşi: | Täze maglumatlary öwretmek sapagy. |
| Sapakda ulanylýan okuw-görkezme esbaplar, sanly serişdeler, paýlama maglumatlar: | Kompýuter, interaktiw tagta, slaýdlar, tanyşdyrmalar, tablisalar, tema degişli soraglar, çyzgyç. |
Sapagyň gidişi:
1. Sapagyň guramaçylyk döwri:
1. Salamlaşmak. Gatnaşygy hasaba almak.
2. Okuwçylaryň ünsüni sapaga gönükdirmek.
3. Syýasy wakalar bilen tanyşdyrmak.
4. Gahryman Arkadagymyzyň «Paýhas çesmesi» «Paýhas çesmesi» kitabyndan sorag-jogap alyşmak.
2. Öý işiniň ýerine ýetirilişini barlamak:
1. Näme üçin birinji meselede x-iň bahasy položitel bolmaly?
2. Ikinji meselede jisim ýerden 25 m beýiklikde näçe gezek bolýar?
(Paraboladan görnüşi ýaly iki gezek 25m beýiklikde bolýar)
3. Geçilen temany jemlemek:
Kwadrat deňlemeleriň kömegi bilen meseleler çözmek
4. Täze temany düşündirmek:
Temany düşündirmegiň meýilnamasy:
1.Kwadrat deňlemäniň kökleriniň formulasy barada umumy düşünje bermek.
2. Kwadrat deňlemeleriň köklerini tapmagy öwretmek
3. Kwadrat deňlemeleriň kömegi bilen meseleler çözmegi öwretmek
Temany öwrenmek bilen okuwçylar bilmeli:
1.Kwadrat deňlemäniň kökleriniň formulasy barada umumy düşünjeleri bilmeli.
2. Kwadrat deňlemeleriň köklerini tapmagy bilmeli
3. Kwadrat deňlemeleriň kömegi bilen meseleler çözmegi bilmeli
Temany öwrenmek bilen okuwçylar başarmaly:
1.Kwadrat deňlemäniň kökleriniň formulasy barada umumy düşünjeleri bilmegi başarmaly
2. Kwadrat deňlemeleriň köklerini tapmagy başarmaly
3. Kwadrat deňlemeleriň kömegi bilen meseleler çözmegi başarmaly
Matematikanyň, fizikanyň, tehnikanyň köp meseleleri kwadrat deňlemeleriň kömegi bilen çözülýär.
1-nji mysal. Bir tarapy beýlekisinden 5 m uly bolan gönüburçlugyň meýdany 84 m2 bolsa, onuň taraplaryny tapyň.
Çözülişi. Goý, gönüburçlugyň bir tarapy x m bolsun. Onda onuň beýleki tarapy (x + 5)m bolar. Şerte görä:
x(x + 5) = 84.
Alnan deňlemäni ýönekeýleşdireliň:
x2 + 5x – 84 = 0.
Bu deňlemäni çözüp, x1 = –12, x2 = 7 kökleri taparys. Meseläniň şertine görä, x položitel san bolmaly. Onda gönüburçlugyň bir tarapy 7m, beýleki tarapy bolsa 7 + 5 = 12 m bolar.
Jogaby: 7 m, 12 m.
386. 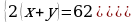
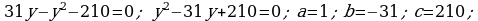
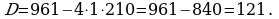
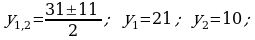
Jogaby: 21 m we 10 m.
5. Täze temany berkitmek:
388. 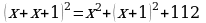
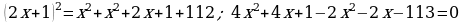
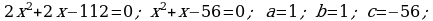
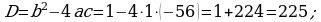
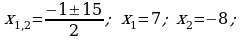
Jogaby: 7 we 8
390. 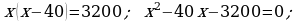
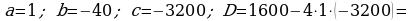
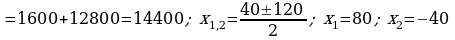
Jogaby: 80 sm we 40 sm.
6. Öý işini tabşyrmak:
1. Näme üçin birinji meselede x-iň bahasy položitel bolmaly?
2. Ikinji meselede jisim ýerden 25 m beýiklikde näçe gezek bolýar?
7. Sapagy jemlemek we okuwçylaryň bilimlerini bahalandyrmak:
Höweslendiriji bahalary goýmak we delillendirmek Okuwçylary delillendirip bahalandyrmak.
Ýazan mugallym: M.Işankulyýew
Bellik:_______________________________________________________________
Barlan: Müdiriň okuw işleri baradaky orunbasary ____________________________
Mekdebi№: 4 Dersiň ady: Algebra
| Synpy: | VIII A | VIII B |
| Senesi: | | |
| Sapagyň temasy: | Gönükme çözmek. |
| Sapagyň maksatlary: | |
| 1)Bilim berijilik maksady: | Kwadrat deňlemeleriň kömegi bilen meseleler çözmegi öwretmek. Okuwçylaryň öňki öwrenenlerini berkitmek, olaryň başarnyklaryny, ukyplaryny ösdürmek. |
| 2) Terbiýeçilik maksady: | Okuwçylary watançylyk, zähmetsöýerlik, beýik adamkärçilik ruhunda terbiýelemek. Olaryň watansöýüjilik duýgularyny ösdürmek. |
| Sapagyň görnüşi: | Täze maglumatlary öwretmek sapagy. |
| Sapakda ulanylýan okuw-görkezme esbaplar, sanly serişdeler, paýlama maglumatlar: | Kompýuter, interaktiw tagta, slaýdlar, tanyşdyrmalar, tablisalar, tema degişli soraglar, çyzgyç. |
Sapagyň gidişi:
1. Sapagyň guramaçylyk döwri:
1. Salamlaşmak. Gatnaşygy hasaba almak.
2. Okuwçylaryň ünsüni sapaga gönükdirmek.
3. Syýasy wakalar bilen tanyşdyrmak.
4. Gahryman Arkadagymyzyň «Paýhas çesmesi» «Paýhas çesmesi» kitabyndan sorag-jogap alyşmak.
2. Öý işiniň ýerine ýetirilişini barlamak:
1. Näme üçin birinji meselede x-iň bahasy položitel bolmaly?
2. Ikinji meselede jisim ýerden 25 m beýiklikde näçe gezek bolýar?
(Paraboladan görnüşi ýaly iki gezek 25m beýiklikde bolýar)
3. Geçilen temany jemlemek:
Kwadrat deňlemeleriň kömegi bilen meseleler çözmek
4. Täze temany düşündirmek:
Temany düşündirmegiň meýilnamasy:
1.Kwadrat deňlemäniň kökleriniň formulasy barada umumy düşünje bermek.
2. Kwadrat deňlemeleriň köklerini tapmagy öwretmek
3. Kwadrat deňlemeleriň kömegi bilen meseleler çözmegi öwretmek
Temany öwrenmek bilen okuwçylar bilmeli:
1.Kwadrat deňlemäniň kökleriniň formulasy barada umumy düşünjeleri bilmeli.
2. Kwadrat deňlemeleriň köklerini tapmagy bilmeli
3. Kwadrat deňlemeleriň kömegi bilen meseleler çözmegi bilmeli
Temany öwrenmek bilen okuwçylar başarmaly:
1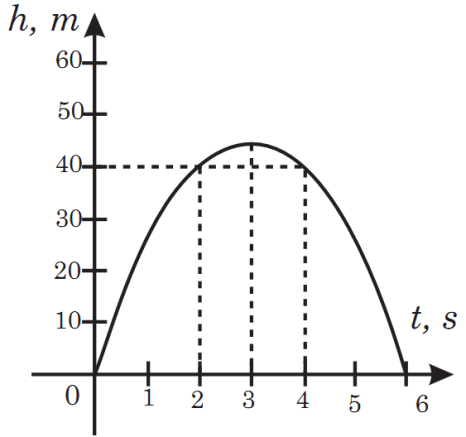 .Kwadrat deňlemäniň kökleriniň formulasy barada umumy düşünjeleri bilmegi başarmaly
.Kwadrat deňlemäniň kökleriniň formulasy barada umumy düşünjeleri bilmegi başarmaly
2. Kwadrat deňlemeleriň köklerini tapmagy başarmaly
3. Kwadrat deňlemeleriň kömegi bilen meseleler çözmegi başarmaly
Matematikanyň, fizikanyň, tehnikanyň köp meseleleri kwadrat deňlemeleriň kömegi bilen çözülýär.
2-nji mysal. Jisim 30 m/s başlangyç tizlik bilen dik ýokary zyňlypdyr. Ol näçe sekuntdan soň 40 m beýiklikde bolar?
Çözülişi. Fizika dersinden belli bolşy ýaly, dik ýokaryk zyňlan jisimiň t sekuntdan soň galýan h beýikligi
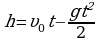
formula bilen tapylýar. Bu ýerde v0 – başlangyç tizlik (m/s), g – takmyny bahasy 10 m/s2-a deň bolan ýokardan erkin gaçma tizlenmesi.
Ýokardaky formulada h = 40 m, v0 = 30 m/s bahalary ornuna goýup alarys:
40 = 30t – 5t2.Bu ýerden:
5t2 – 30t + 40 = 0, t2 – 6t + 8 = 0.
Bu kwadrat deňlemäni çözüp t1 =2, t2 = 4 bahalary tapýarys. Tapylan kökleriň manysyna düşünmek üçin h = 30t – 5t2 baglylygyň grafigine seredeliň (8nji surat). Grafikden görnüşi ýaly, zyňlan jisim ilkinji 3 sekundyň dowamynda
45 me çenli ýokaryk galýar, soňra bolsa ol aşaklap, 6 sekuntdan soň ýere düşýär.
Şeýlelikde, jisim zyňlandan 2 sekuntdan we 4 sekuntdan soňra ýerden 40 m beýiklige galar.
Jogaby: jisim zyňlandan 2 sekuntdan we 4 sekuntdan soňra 40 m beýiklikde bolar.
392. 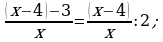
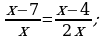
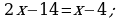
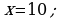
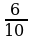 .
.
5. Täze temany berkitmek:
394. 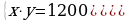
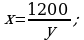
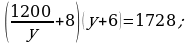
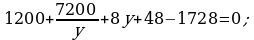
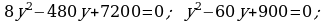
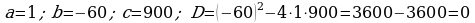
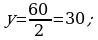
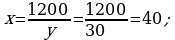
Jogaby: 30 we 40.
396. 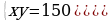
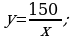
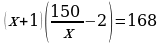
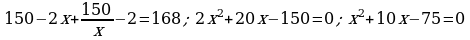
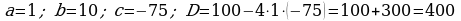
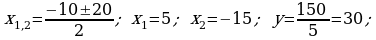
Jogaby: 6 awtobus.
6. Öý işini tabşyrmak:
1. Näme üçin birinji meselede x-iň bahasy položitel bolmaly?
2. Ikinji meselede jisim ýerden 25 m beýiklikde näçe gezek bolýar?
7. Sapagy jemlemek we okuwçylaryň bilimlerini bahalandyrmak:
Höweslendiriji bahalary goýmak we delillendirmek Okuwçylary delillendirip bahalandyrmak.
Ýazan mugallym: M.Işankulyýew
Bellik:_______________________________________________________________
Barlan: Müdiriň okuw işleri baradaky orunbasary ____________________________
Mekdebi№: 4 Dersiň ady: Algebra
| Synpy: | VIII A | VIII B |
| Senesi: | | |
| Sapagyň temasy: | Türkmenistanyň durmuş-ykdysady taýdan ösüşine degişli meseleleriň kwadrat deňlemeleriň kömegi bilen çözülişi |
| Sapagyň maksatlary: | |
| 1)Bilim berijilik maksady: | Türkmenistanyň durmuş-ykdysady taýdan ösüşine degişli meseleleriň kwadrat deňlemeleriň kömegi bilen çözülişi öwretmek. Okuwçylaryň öňki öwrenenlerini berkitmek, olaryň başarnyklaryny, ukyplaryny ösdürmek. |
| 2) Terbiýeçilik maksady: | Okuwçylary watançylyk, zähmetsöýerlik, beýik adamkärçilik ruhunda terbiýelemek. Olaryň watansöýüjilik duýgularyny ösdürmek. |
| Sapagyň görnüşi: | Täze maglumatlary öwretmek sapagy. |
| Sapakda ulanylýan okuw-görkezme esbaplar, sanly serişdeler, paýlama maglumatlar: | Kompýuter, interaktiw tagta, slaýdlar, tanyşdyrmalar, tablisalar, tema degişli soraglar, çyzgyç. |
Sapagyň gidişi:
1. Sapagyň guramaçylyk döwri:
1. Salamlaşmak. Gatnaşygy hasaba almak.
2. Okuwçylaryň ünsüni sapaga gönükdirmek.
3. Syýasy wakalar bilen tanyşdyrmak.
4. Gahryman Arkadagymyzyň «Paýhas çesmesi» «Paýhas çesmesi» kitabyndan sorag-jogap alyşmak.
2. Öý işiniň ýerine ýetirilişini barlamak:
1. Näme üçin birinji meselede x-iň bahasy položitel bolmaly?
2. Ikinji meselede jisim ýerden 25 m beýiklikde näçe gezek bolýar?
(Paraboladan görnüşi ýaly iki gezek 25m beýiklikde bolýar)
3. Geçilen temany jemlemek:
Kwadrat deňlemeleriň kömegi bilen meseleler çözmek
4. Täze temany düşündirmek:
Temany düşündirmegiň meýilnamasy:
1.Kwadrat deňlemäniň kökleriniň formulasy barada umumy düşünje bermek.
2. Kwadrat deňlemeleriň köklerini tapmagy öwretmek
3. Kwadrat deňlemeleriň kömegi bilen meseleler çözmegi öwretmek
Temany öwrenmek bilen okuwçylar bilmeli:
1.Kwadrat deňlemäniň kökleriniň formulasy barada umumy düşünjeleri bilmeli.
2. Kwadrat deňlemeleriň köklerini tapmagy bilmeli
3. Kwadrat deňlemeleriň kömegi bilen meseleler çözmegi bilmeli
Temany öwrenmek bilen okuwçylar başarmaly:
1.Kwadrat deňlemäniň kökleriniň formulasy barada umumy düşünjeleri bilmegi başarmaly
2. Kwadrat deňlemeleriň köklerini tapmagy başarmaly
3. Kwadrat deňlemeleriň kömegi bilen meseleler çözmegi başarmaly
398. 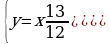
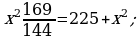
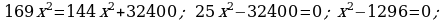
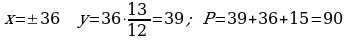
Jogaby: 90 sm
400. 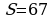 km;
km; 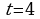 sag;
sag; 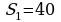 km;
km; 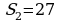 km;
km;
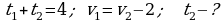
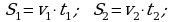
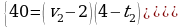
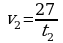
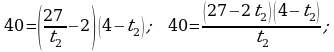
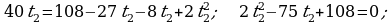
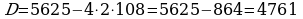
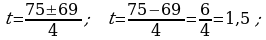 Jogaby: 1,5 sagat.
Jogaby: 1,5 sagat.
5. Täze temany berkitmek:
402. 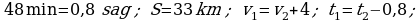
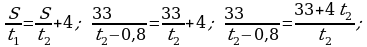
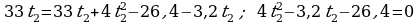
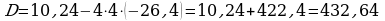
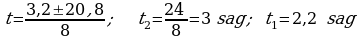
Jogaby: 3 sag we 2,2 sag
404. Gaýygyň köldäki tizligi 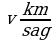 . Derýadaky tizligi
. Derýadaky tizligi 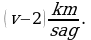 Gaýygyň derýadaky sarp eden wagty
Gaýygyň derýadaky sarp eden wagty 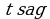 , köldäki sarp eden wagty
, köldäki sarp eden wagty 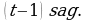
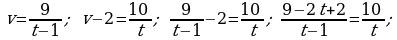
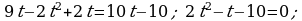
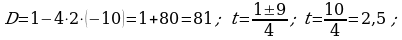
Jogaby: 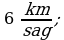
6. Öý işini tabşyrmak:
1. Näme üçin birinji meselede x-iň bahasy položitel bolmaly?
2. Ikinji meselede jisim ýerden 25 m beýiklikde näçe gezek bolýar?
7. Sapagy jemlemek we okuwçylaryň bilimlerini bahalandyrmak:
Höweslendiriji bahalary goýmak we delillendirmek Okuwçylary delillendirip bahalandyrmak.
Ýazan mugallym: M.Işankulyýew
Bellik:_______________________________________________________________
Barlan: Müdiriň okuw işleri baradaky orunbasary ____________________________
Mekdebi№: 4 Dersiň ady: Algebra
| Synpy: | VIII A | VIII B |
| Senesi: | | |
| Sapagyň temasy: | Drobly rasional deňlemeleri çözmek |
| Sapagyň maksatlary: | |
| 1)Bilim berijilik maksady: | Drobly rasional deňlemeleri çözmegi öwretmek. Okuwçylaryň öňki öwrenenlerini berkitmek, olaryň başarnyklaryny, ukyplaryny ösdürmek. |
| 2) Terbiýeçilik maksady: | Okuwçylary watançylyk, zähmetsöýerlik, beýik adamkärçilik ruhunda terbiýelemek. Olaryň watansöýüjilik duýgularyny ösdürmek. |
| Sapagyň görnüşi: | Täze maglumatlary öwretmek sapagy. |
| Sapakda ulanylýan okuw-görkezme esbaplar, sanly serişdeler, paýlama maglumatlar: | Kompýuter, interaktiw tagta, slaýdlar, tanyşdyrmalar, tablisalar, tema degişli soraglar, çyzgyç. |
Sapagyň gidişi:
1. Sapagyň guramaçylyk döwri:
1. Salamlaşmak. Gatnaşygy hasaba almak.
2. Okuwçylaryň ünsüni sapaga gönükdirmek.
3. Syýasy wakalar bilen tanyşdyrmak.
4. Gahryman Arkadagymyzyň «Paýhas çesmesi» «Paýhas çesmesi» kitabyndan sorag-jogap alyşmak.
2. Öý işiniň ýerine ýetirilişini barlamak:
1. Näme üçin birinji meselede x-iň bahasy položitel bolmaly?
2. Ikinji meselede jisim ýerden 25 m beýiklikde näçe gezek bolýar?
(Paraboladan görnüşi ýaly iki gezek 25m beýiklikde bolýar)
3. Geçilen temany jemlemek:
Kwadrat deňlemeleriň kömegi bilen meseleler çözmek
4. Täze temany düşündirmek:
Temany düşündirmegiň meýilnamasy:
1. Drobly rasional deňlemeleri çözmek barada umumy düşünje bermek.
2. Rasional deňlemeler barada öwretmek
3. Bitin rasional deňlemeler barada düşünje bermek
Temany öwrenmek bilen okuwçylar bilmeli:
1. Drobly rasional deňlemeleri çözmek barada umumy düşünjeleri bilmeli.
2. Rasional deňlemeler barada bilmeli
3. Bitin rasional deňlemeler barada düşünjeleri bilmeli
Temany öwrenmek bilen okuwçylar başarmaly:
1. Drobly rasional deňlemeleri çözmek barada umumy düşünjeleri bilmegi başarmaly.
2. Rasional deňlemeleri çözmegi başarmaly
3. Drobly rasional deňlemeleri çözmegi başarmaly
Siz drob aňlatmalar we algebraik droblar bilen tanyş bolupdyňyz. Düzüminde algebraik droblar bolan deňlemelere drobly rasional deňlemeler diýilýär.
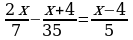 bitin deňlemäni çözeliň.
bitin deňlemäni çözeliň.
Deňlemäniň iki bölegini hem oňa girýän droblaryň iň kiçi umumy maýdalawjysyna, ýagny 35-e köpeldeliň.
Berlen deňlemä deňgüýçli bolan bitin koeffisiýentli deňleme alarys:
5 ∙ 2x–(x + 4) = 7(x – 4).
Bu deňlemäni çözüp, taparys: x = 2.
Drobly rasional deňlemeler çözülende aşakdaky düzgüni berjaý etmeklik maslahat berilýär:
1) deňlemä girýän droblaryň iň kiçi umumy maýdalawjysyny tapmaly;
2) deňlemäniň iki bölegini hem şol umumy maýdalawja köpeltmeli;
3) alnan bitin deňlemäni çözmeli;
4) onuň kökleriniň umumy maýdalawjyny nola öwürmeýänlerini almaly.
5. Täze temany berkitmek:
434. b) 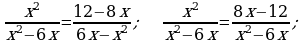
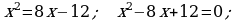
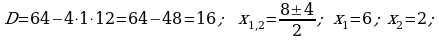
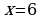 bolanda berlen deňlemäniň maýdalawjysy nola deň bolýar. Şonuň üçinem
bolanda berlen deňlemäniň maýdalawjysy nola deň bolýar. Şonuň üçinem 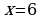 berlen deňlemäniň köki bolup bilmez.
berlen deňlemäniň köki bolup bilmez.
Jogaby: 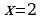
e) 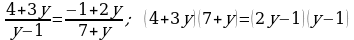
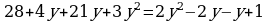
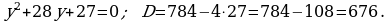
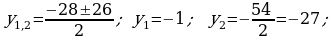
435. d) 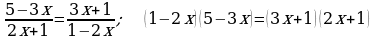
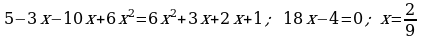
e) 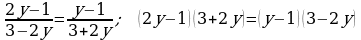
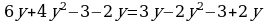
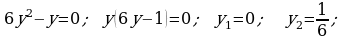
6. Öý işini tabşyrmak:
1. Rasional deňlemeler diýlip nähili deňlemelere aýdylýar?
2. Bitin rasional deňleme diýlip nähili deňlemä aýdylýar?
3. Drobly rasional deňleme diýlip nähili deňlemä aýdylýar?
4. Drobly rasional deňlemeler nähili çözülýär?
7. Sapagy jemlemek we okuwçylaryň bilimlerini bahalandyrmak:
Höweslendiriji bahalary goýmak we delillendirmek Okuwçylary delillendirip bahalandyrmak.
Ýazan mugallym: M.Işankulyýew
Bellik:_______________________________________________________________
Barlan: Müdiriň okuw işleri baradaky orunbasary ____________________________
Mekdebi№: 4 Dersiň ady: Algebra
| Synpy: | VIII A | VIII B |
| Senesi: | | |
| Sapagyň temasy: | Gönükme çözmek. |
| Sapagyň maksatlary: | |
| 1)Bilim berijilik maksady: | Drobly rasional deňlemeleri çözmegi öwretmek. Okuwçylaryň öňki öwrenenlerini berkitmek, olaryň başarnyklaryny, ukyplaryny ösdürmek. |
| 2) Terbiýeçilik maksady: | Okuwçylary watançylyk, zähmetsöýerlik, beýik adamkärçilik ruhunda terbiýelemek. Olaryň watansöýüjilik duýgularyny ösdürmek. |
| Sapagyň görnüşi: | Täze maglumatlary öwretmek sapagy. |
| Sapakda ulanylýan okuw-görkezme esbaplar, sanly serişdeler, paýlama maglumatlar: | Kompýuter, interaktiw tagta, slaýdlar, tanyşdyrmalar, tablisalar, tema degişli soraglar, çyzgyç. |
Sapagyň gidişi:
1. Sapagyň guramaçylyk döwri:
1. Salamlaşmak. Gatnaşygy hasaba almak.
2. Okuwçylaryň ünsüni sapaga gönükdirmek.
3. Syýasy wakalar bilen tanyşdyrmak.
4. Gahryman Arkadagymyzyň «Paýhas çesmesi» «Paýhas çesmesi» kitabyndan sorag-jogap alyşmak.
2. Öý işiniň ýerine ýetirilişini barlamak:
1. Rasional deňlemeler diýlip nähili deňlemelere aýdylýar?
2. Bitin rasional deňleme diýlip nähili deňlemä aýdylýar?
3. Drobly rasional deňleme diýlip nähili deňlemä aýdylýar?
4. Drobly rasional deňlemeler nähili çözülýär?
3. Geçilen temany jemlemek:
Drobly rasional deňlemeleri çözmek
4. Täze temany düşündirmek:
Temany düşündirmegiň meýilnamasy:
1. Drobly rasional deňlemeleri çözmek barada umumy düşünje bermek.
2. Rasional deňlemeler barada öwretmek
3. Bitin rasional deňlemeler barada düşünje bermek
Temany öwrenmek bilen okuwçylar bilmeli:
1. Drobly rasional deňlemeleri çözmek barada umumy düşünjeleri bilmeli.
2. Rasional deňlemeler barada bilmeli
3. Bitin rasional deňlemeler barada düşünjeleri bilmeli
Temany öwrenmek bilen okuwçylar başarmaly:
1. Drobly rasional deňlemeleri çözmek barada umumy düşünjeleri bilmegi başarmaly.
2. Rasional deňlemeleri çözmegi başarmaly
3. Drobly rasional deňlemeleri çözmegi başarmaly
Siz drob aňlatmalar we algebraik droblar bilen tanyş bolupdyňyz. Düzüminde algebraik droblar bolan deňlemelere drobly rasional deňlemeler diýilýär.
Drobly rasional deňlemeler çözülende aşakdaky düzgüni berjaý etmeklik maslahat berilýär:
1) deňlemä girýän droblaryň iň kiçi umumy maýdalawjysyny tapmaly;
2) deňlemäniň iki bölegini hem şol umumy maýdalawja köpeltmeli;
3) alnan bitin deňlemäni çözmeli;
4) onuň kökleriniň umumy maýdalawjyny nola öwürmeýänlerini almaly.
436. a) 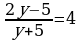 ;
; 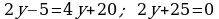

d) 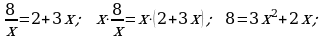
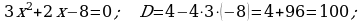
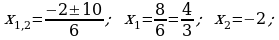
ä) 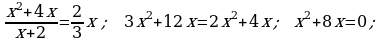
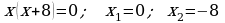
5. Täze temany berkitmek:
437. a) 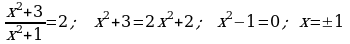
e) 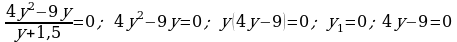
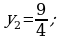
ä) 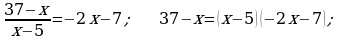
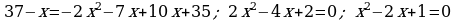
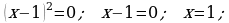
6. Öý işini tabşyrmak:
Mysal N 438
7. Sapagy jemlemek we okuwçylaryň bilimlerini bahalandyrmak:
Höweslendiriji bahalary goýmak we delillendirmek Okuwçylary delillendirip bahalandyrmak.
Ýazan mugallym: M.Işankulyýew
Bellik:_______________________________________________________________
Barlan: Müdiriň okuw işleri baradaky orunbasary ____________________________
Mekdebi№: 4 Dersiň ady: Algebra
| Synpy: | VIII A | VIII B |
| Senesi: | | |
| Sapagyň temasy: | Drobly rasional deňlemeleriň kömegi bilen meseleleriň çözülişi |
| Sapagyň maksatlary: | |
| 1)Bilim berijilik maksady: | Drobly rasional deňlemeleriň kömegi bilen meseleleriň çözülişini öwretmek. Okuwçylaryň öňki öwrenenlerini berkitmek, olaryň başarnyklaryny, ukyplaryny ösdürmek. |
| 2) Terbiýeçilik maksady: | Okuwçylary watançylyk, zähmetsöýerlik, beýik adamkärçilik ruhunda terbiýelemek. Olaryň watansöýüjilik duýgularyny ösdürmek. |
| Sapagyň görnüşi: | Täze maglumatlary öwretmek sapagy. |
| Sapakda ulanylýan okuw-görkezme esbaplar, sanly serişdeler, paýlama maglumatlar: | Kompýuter, interaktiw tagta, slaýdlar, tanyşdyrmalar, tablisalar, tema degişli soraglar, çyzgyç. |
Sapagyň gidişi:
1. Sapagyň guramaçylyk döwri:
1. Salamlaşmak. Gatnaşygy hasaba almak.
2. Okuwçylaryň ünsüni sapaga gönükdirmek.
3. Syýasy wakalar bilen tanyşdyrmak.
4. Gahryman Arkadagymyzyň «Paýhas çesmesi» «Paýhas çesmesi» kitabyndan sorag-jogap alyşmak.
2. Öý işiniň ýerine ýetirilişini barlamak:
438. d) 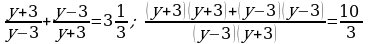
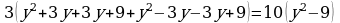
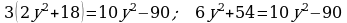
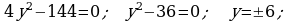
3. Geçilen temany jemlemek:
Drobly rasional deňlemeleri çözmek
4. Täze temany düşündirmek:
Temany düşündirmegiň meýilnamasy:
1. Drobly rasional deňlemeleri çözmek barada umumy düşünje bermek.
2. Rasional deňlemeler barada öwretmek
3. Drobly rasional deňlemeleriň kömegi bilen meseleleriň çözülişi barada düşünje bermek
Temany öwrenmek bilen okuwçylar bilmeli:
1. Drobly rasional deňlemeleri çözmek barada umumy düşünjeleri bilmeli.
2. Rasional deňlemeler barada bilmeli
3. Drobly rasional deňlemeleriň kömegi bilen meseleleriň çözülişi barada bilmeli
Temany öwrenmek bilen okuwçylar başarmaly:
1. Drobly rasional deňlemeleri çözmek barada umumy düşünjeleri bilmekligi başarmaly.
2. Rasional deňlemeler barada bilmegi başarmaly
3. Drobly rasional deňlemeleriň kömegi bilen meseleleri çöümegi başarmaly
Drobly rasional deňlemäniň kömegi bilen çözüp bolýan meseleleriň birnäçesine seredip geçeliň.
1-nji mesele. Şäherden 240 km uzaklykda ýerleşýän oba tarap şol bir wagtda ýeňil maşyn we ýük maşyny çykyp ugrady. Ýeňil maşynyň tizligi ýük maşynyň tizliginden 20 km/sag köp bolup, ol oba ýük maşynyndan 1 sag öň geldi. Her maşynyň tizligini tapyň.
Çözülişi. Goý, x km/sag ýük maşynyň tizligi bolsun. Onda ýeňil maşynyň tizligi (x + 20) km/sag bolar.
Ýük maşyny 240 km ýoly geçmek üçin 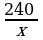 sag, ýeňil maşyn bolsa, şol ýola sag sarp edipdir
sag, ýeňil maşyn bolsa, şol ýola sag sarp edipdir
Meseläniň şertine görä ýeňil maşyn oba ýük maşyndan 1 sag öň gelipdir.
Diýmek, 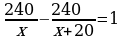
Alnan drobly rasional deňlemäni çözmek bilen, onuň köklerini tapýarys: x1 = 60, x2 = –80.
Diýmek, ýük maşynyň tizligi 60 km/sag, ýeňil maşynyň tizligi bolsa 60 + 20 = 80 km/sag.
Jogaby: 60 km/sag we 80 km/sag.
5. Täze temany berkitmek:
447-nji gönükme
Gysgalmaýan ady drobuň sanawjysy onuň maýdalawjysyndan 5 san kiçi. Eger ol drobuň sanawjysy 2 san kiçeldilip, maýdalawjysy bolsa 16 san ulaldylsa, onda drob 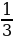 san kiçeler. Ol droby tapyň.
san kiçeler. Ol droby tapyň.
Çözülişi:
x gysgalmaýan ady drobuň maýdalawjysy. (x + 5) gysgalmaýan ady drobuň sanawjysy
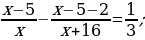
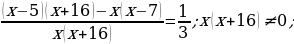
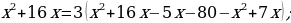
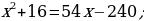
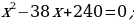
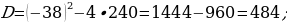
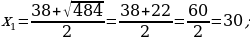
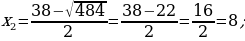
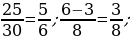
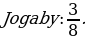
6. Öý işini tabşyrmak:
1. 1-nji meseledäki drobly rasional deňleme nähili çözülýär?
2. 2-nji meseledäki drobly rasional deňleme nähili çözülýär?
7. Sapagy jemlemek we okuwçylaryň bilimlerini bahalandyrmak:
Höweslendiriji bahalary goýmak we delillendirmek Okuwçylary delillendirip bahalandyrmak.
Ýazan mugallym: M.Işankulyýew
Bellik:_______________________________________________________________
Barlan: Müdiriň okuw işleri baradaky orunbasary ____________________________
Mekdebi№: 4 Dersiň ady: Algebra
| Synpy: | VIII A | VIII B |
| Senesi: | | |
| Sapagyň temasy: | Gönükme çözmek. |
| Sapagyň maksatlary: | |
| 1)Bilim berijilik maksady: | Drobly rasional deňlemeleriň kömegi bilen meseleleriň çözülişini öwretmek. Okuwçylaryň öňki öwrenenlerini berkitmek, olaryň başarnyklaryny, ukyplaryny ösdürmek. |
| 2) Terbiýeçilik maksady: | Okuwçylary watançylyk, zähmetsöýerlik, beýik adamkärçilik ruhunda terbiýelemek. Olaryň watansöýüjilik duýgularyny ösdürmek. |
| Sapagyň görnüşi: | Täze maglumatlary öwretmek sapagy. |
| Sapakda ulanylýan okuw-görkezme esbaplar, sanly serişdeler, paýlama maglumatlar: | Kompýuter, interaktiw tagta, slaýdlar, tanyşdyrmalar, tablisalar, tema degişli soraglar, çyzgyç. |
Sapagyň gidişi:
1. Sapagyň guramaçylyk döwri:
1. Salamlaşmak. Gatnaşygy hasaba almak.
2. Okuwçylaryň ünsüni sapaga gönükdirmek.
3. Syýasy wakalar bilen tanyşdyrmak.
4. Gahryman Arkadagymyzyň «Paýhas çesmesi» «Paýhas çesmesi» kitabyndan sorag-jogap alyşmak.
2. Öý işiniň ýerine ýetirilişini barlamak:
1. 1-nji meseledäki drobly rasional deňleme nähili çözülýär?
2. 2-nji meseledäki drobly rasional deňleme nähili çözülýär?
3. Geçilen temany jemlemek:
Drobly rasional deňlemeleriň kömegi bilen meseleleriň çözülişi
4. Täze temany düşündirmek:
Temany düşündirmegiň meýilnamasy:
1. Drobly rasional deňlemeleri çözmek barada umumy düşünje bermek.
2. Rasional deňlemeler barada öwretmek
3. Drobly rasional deňlemeleriň kömegi bilen meseleleriň çözülişi barada düşünje bermek
Temany öwrenmek bilen okuwçylar bilmeli:
1. Drobly rasional deňlemeleri çözmek barada umumy düşünjeleri bilmeli.
2. Rasional deňlemeler barada bilmeli
3. Drobly rasional deňlemeleriň kömegi bilen meseleleriň çözülişi barada bilmeli
Temany öwrenmek bilen okuwçylar başarmaly:
1. Drobly rasional deňlemeleri çözmek barada umumy düşünjeleri bilmekligi başarmaly.
2. Rasional deňlemeler barada bilmegi başarmaly
3. Drobly rasional deňlemeleriň kömegi bilen meseleleri çöümegi başarmaly
Drobly rasional deňlemäniň kömegi bilen çözüp bolýan meseleleriň birnäçesine seredip geçeliň.
1-nji mesele. Şäherden 240 km uzaklykda ýerleşýän oba tarap şol bir wagtda ýeňil maşyn we ýük maşyny çykyp ugrady. Ýeňil maşynyň tizligi ýük maşynyň tizliginden 20 km/sag köp bolup, ol oba ýük maşynyndan 1 sag öň geldi. Her maşynyň tizligini tapyň.
Çözülişi. Goý, x km/sag ýük maşynyň tizligi bolsun. Onda ýeňil maşynyň tizligi (x + 20) km/sag bolar.
Ýük maşyny 240 km ýoly geçmek üçin 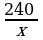 sag, ýeňil maşyn bolsa, şol ýola sag sarp edipdir
sag, ýeňil maşyn bolsa, şol ýola sag sarp edipdir
Meseläniň şertine görä ýeňil maşyn oba ýük maşyndan 1 sag öň gelipdir.
Diýmek, 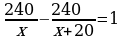
Alnan drobly rasional deňlemäni çözmek bilen, onuň köklerini tapýarys: x1 = 60, x2 = –80.
Diýmek, ýük maşynyň tizligi 60 km/sag, ýeňil maşynyň tizligi bolsa 60 + 20 = 80 km/sag.
Jogaby: 60 km/sag we 80 km/sag.
2-nji mesele. Aman derýada gaýyk bilen akymyň garşysyna 6 km we kölde 15 km aralygy geçipdir. Ol kölde geçen ýoluna derýada geçen ýoly üçin sarp eden wagtyndan 1 sagat köp sarp edipdir. Eger derýanyň akyş tizligi 2 km/sag bolsa, gaýygyň köldäki tizligini tapyň.
Çözülişi. Goý, gaýygyň köldäki (akmaýan suwdaky) tizligi x km/sag bolsun. Onda onuň akymyň garşysyna gidendäki tizligi (x – 2) km/sag bolar.
Gaýygyň akymyň garşysyna ýüzen wagty 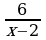 kölde ýüzen
kölde ýüzen 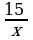 aňlatmalar görnüşinde ýazylýar. Meseläniň şertine görä:
aňlatmalar görnüşinde ýazylýar. Meseläniň şertine görä:
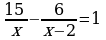
Bu deňlemäni çözüp, onuň köklerini tapýarys:
x1 = 5, x2 = 6.
Meseläniň şertini 5 we 6 kökleriň ikisi-de kanagatlandyrýar. Jogaby: 5 km/sag ýa-da 6 km/sag.
5. Täze temany berkitmek:
446. 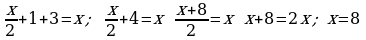
448. 2-nji maşynyň tizligi 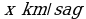 , 1-nji maşynyň tizligi
, 1-nji maşynyň tizligi 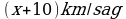
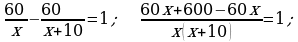
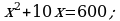
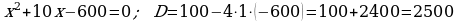
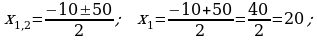
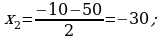 Jogaby: 30 we 20 km/sag.
Jogaby: 30 we 20 km/sag.
6. Öý işini tabşyrmak:
1. 1-nji meseledäki drobly rasional deňleme nähili çözülýär?
2. 2-nji meseledäki drobly rasional deňleme nähili çözülýär?
7. Sapagy jemlemek we okuwçylaryň bilimlerini bahalandyrmak:
Höweslendiriji bahalary goýmak we delillendirmek Okuwçylary delillendirip bahalandyrmak.
Ýazan mugallym: M.Işankulyýew
Bellik:_______________________________________________________________
Barlan: Müdiriň okuw işleri baradaky orunbasary ____________________________
Mekdebi№: 4 Dersiň ady: Algebra
| Synpy: | VIII A | VIII B |
| Senesi: | | |
| Sapagyň temasy: | 5-nji ýazuw- barlag işi |
| Sapagyň maksady. | |
| 1) Bilim berijilik maksady: | Okuwçylaryň bilimini barlamak, pikirleniş endiklerini ösdürmek |
| 2) Terbiýeçilik maksady: | Okuwçylary watançylyk, zähmetsöýerlik, beýik adamkärçilik ruhunda terbiýelemek. Olaryň watansöýüjilik duýgularyny ösdürmek. |
| Sapagyň görnüşi: | Ýazuw-barlag işi geçirilýän sapak |
| Sapakda ulanylýan okuw-görkezme esbaplar, sanly serişdeler, paýlama maglumatlar: | Barlag iş depderleri |
Sapagyň gidişi:
1. Sapagyň guramaçylyk döwri:
1. Salamlaşmak. Gatnaşygy hasaba almak. 2. Okuwçylaryň sapaga taýýarlygyny barlamak.
3. Okuwçylaryň ünsüni sapaga gönükdirmek. 4. Syýasy wakalar bilen tanyşdyrmak.
2. Ýazuw-barlag işiniň mazmunyny düşündirmek.
Çep tarap
1) Deňlemäniň kökleriniň jemini we köpeltmek hasylyny tapyň:
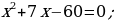
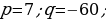
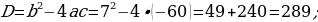
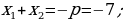
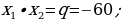
2) Mesele çözüň.
Uzynlygy ininden 11 sm uly, meýdany 210 sm2 bolan gönüburçlygyň taraplaryny tapyň.
Çözülişi:
x gönüburçlugyň ini;
(x + 11) gönüburçlugyň uzynlygy;
x(x + 11) gönüburçlugyň meýdany;
x(x + 11) = 210
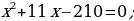
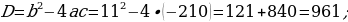
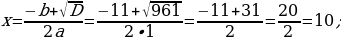
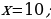
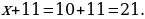
Jogaby: Gönüburçlugyň ini 10 sm, uzunlygy 21 sm.
Sag tarap
1) Deňlemäniň kökleriniň jemini we köpeltmek hasylyny tapyň:
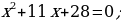
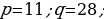
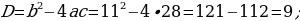
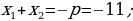
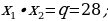
2) Mesele çözüň.
Uzynlygy ininden 4 sm uly, meýdany 60 sm2 bolan gönüburçlygyň taraplaryny tapyň.
Çözülişi:
a gönüburçlugyň ini;
(a + 4) gönüburçlugyň uzynlygy;
a(a + 4) gönüburçlugyň meýdany;
a(a + 4) = 60
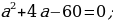
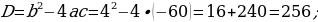
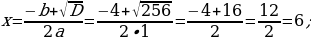
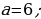
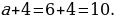
Jogaby: Gönüburçlugyň ini 6 sm, uzunlygy 10 sm.
3. Okuwçylar tarapyndan ýazuw-barlag işiniň ýerine ýetirilmegi.
4. Sapagy jemlemek, öý işini tabşyrmak.
Okuwçylaryň depderlerini toplap almak. Sapagy umumylaşdyryp jemlemek.
Ýazan mugallym: M.Işankulyýew_
Bellik:________________________________________________________________
Barlan: Müdiriň okuw işleri baradaky orunbasary ____________________________
Mekdebi№: 4 Dersiň ady: Algebra
| Synpy: | VIII A | VIII B |
| Senesi: | | |
| Sapagyň temasy: | Drobly rasional deňlemeleriň kömegi bilen meseleleriň çözülişi |
| Sapagyň maksatlary: | |
| 1)Bilim berijilik maksady: | Drobly rasional deňlemeleriň kömegi bilen meseleleriň çözülişini öwretmek. Okuwçylaryň öňki öwrenenlerini berkitmek, olaryň başarnyklaryny, ukyplaryny ösdürmek. |
| 2) Terbiýeçilik maksady: | Okuwçylary watançylyk, zähmetsöýerlik, beýik adamkärçilik ruhunda terbiýelemek. Olaryň watansöýüjilik duýgularyny ösdürmek. |
| Sapagyň görnüşi: | Täze maglumatlary öwretmek sapagy. |
| Sapakda ulanylýan okuw-görkezme esbaplar, sanly serişdeler, paýlama maglumatlar: | Kompýuter, interaktiw tagta, slaýdlar, tanyşdyrmalar, tablisalar, tema degişli soraglar, çyzgyç. |
Sapagyň gidişi:
1. Sapagyň guramaçylyk döwri:
1. Salamlaşmak. Gatnaşygy hasaba almak.
2. Okuwçylaryň ünsüni sapaga gönükdirmek.
3. Syýasy wakalar bilen tanyşdyrmak.
4. Gahryman Arkadagymyzyň «Paýhas çesmesi» «Paýhas çesmesi» kitabyndan sorag-jogap alyşmak.
2. Öý işiniň ýerine ýetirilişini barlamak:
1. 1-nji meseledäki drobly rasional deňleme nähili çözülýär?
2. 2-nji meseledäki drobly rasional deňleme nähili çözülýär?
3. Geçilen temany jemlemek:
5-nji ýazuw- barlag işi
4. Täze temany düşündirmek:
Temany düşündirmegiň meýilnamasy:
1. Drobly rasional deňlemeleri çözmek barada umumy düşünje bermek.
2. Rasional deňlemeler barada öwretmek
3. Drobly rasional deňlemeleriň kömegi bilen meseleleriň çözülişi barada düşünje bermek
Temany öwrenmek bilen okuwçylar bilmeli:
1. Drobly rasional deňlemeleri çözmek barada umumy düşünjeleri bilmeli.
2. Rasional deňlemeler barada bilmeli
3. Drobly rasional deňlemeleriň kömegi bilen meseleleriň çözülişi barada bilmeli
Temany öwrenmek bilen okuwçylar başarmaly:
1. Drobly rasional deňlemeleri çözmek barada umumy düşünjeleri bilmekligi başarmaly.
2. Rasional deňlemeler barada bilmegi başarmaly
3. Drobly rasional deňlemeleriň kömegi bilen meseleleri çöümegi başarmaly
450-nji gönükme
Ýata suwda tizligi 15 km/sag, bolan motorly gaýykakymyň ugruna 35 km, akymyň garşysyna bolsa 25 km geçipdir. Ol akymyň garşysyna geçen ýoluna näçe wagt sarp eden bolsa, akymyň ugruna geçen ýoluna hem şonça wagt sarp edipdir. Derýanyň akyş tizligi näçe?
Çözülişi:
Derýanyň akyş tizligi x km/sag
x gysgalmaýan ady drobuň maýdalawjysy. (x + 5) gysgalmaýan ady drobuň sanawjysy
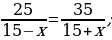
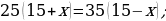
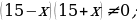
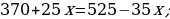
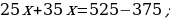
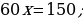
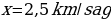
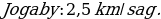
5. Täze temany berkitmek:
452. 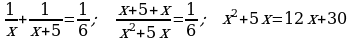
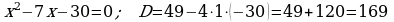
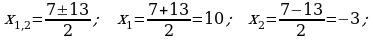
Jogaby: 10 we 15 sag
6. Öý işini tabşyrmak:
1. 1-nji meseledäki drobly rasional deňleme nähili çözülýär?
2. 2-nji meseledäki drobly rasional deňleme nähili çözülýär?
7. Sapagy jemlemek we okuwçylaryň bilimlerini bahalandyrmak:
Höweslendiriji bahalary goýmak we delillendirmek Okuwçylary delillendirip bahalandyrmak.
Ýazan mugallym: M.Işankulyýew
Bellik:_______________________________________________________________
Barlan: Müdiriň okuw işleri baradaky orunbasary ____________________________
Mekdebi№: 4 Dersiň ady: Algebra
| Synpy: | VIII A | VIII B |
| Senesi: | | |
| Sapagyň temasy: | San deňsizlikleri we olaryň häsiýetleri |
| Sapagyň maksatlary: | |
| 1)Bilim berijilik maksady: | San deňsizlikleri we olaryň häsiýetlerini öwretmek. Okuwçylaryň öňki öwrenenlerini berkitmek, olaryň başarnyklaryny, ukyplaryny ösdürmek. |
| 2) Terbiýeçilik maksady: | Okuwçylary watançylyk, zähmetsöýerlik, beýik adamkärçilik ruhunda terbiýelemek. Olaryň watansöýüjilik duýgularyny ösdürmek. |
| Sapagyň görnüşi: | Täze maglumatlary öwretmek sapagy. |
| Sapakda ulanylýan okuw-görkezme esbaplar, sanly serişdeler, paýlama maglumatlar: | Kompýuter, interaktiw tagta, slaýdlar, tanyşdyrmalar, tablisalar, tema degişli soraglar, çyzgyç. |
Sapagyň gidişi:
1. Sapagyň guramaçylyk döwri:
1. Salamlaşmak. Gatnaşygy hasaba almak.
2. Okuwçylaryň ünsüni sapaga gönükdirmek.
3. Syýasy wakalar bilen tanyşdyrmak.
4. Gahryman Arkadagymyzyň «Paýhas çesmesi» «Paýhas çesmesi» kitabyndan sorag-jogap alyşmak.
2. Öý işiniň ýerine ýetirilişini barlamak:
1. 1-nji meseledäki drobly rasional deňleme nähili çözülýär?
2. 2-nji meseledäki drobly rasional deňleme nähili çözülýär?
3. Geçilen temany jemlemek:
Drobly rasional deňlemeleriň kömegi bilen meseleleriň çözülişi
4. Täze temany düşündirmek:
Temany düşündirmegiň meýilnamasy:
1. San deňsizlikleri barada umumy düşünje bermek.
2. Sanlary deňeşdirmegiň usullary barada öwretmek
3. Deňsizlikleriň häsiýetlerini öwretmek
Temany öwrenmek bilen okuwçylar bilmeli:
1. San deňsizlikleri barada umumy düşünjeleri bilmeli
2. Sanlary deňeşdirmegiň usullary barada bilmeli
3. Deňsizlikleriň häsiýetlerini bilmeli
Temany öwrenmek bilen okuwçylar başarmaly:
1. San deňsizlikleri barada umumy düşünjeleri bilmegi başarmaly
2. Sanlary deňeşdirmegiň usullary barada bilmegi başarmaly
3. Deňsizlikleriň häsiýetlerinden peýdalanmagy başarmaly
Biz =, belgileri peýdalanyp, a we b islendik sanlary deňeşdirip bilýäris. Deňeşdirmäniň netijesi deňlik (a = b) ýa-da deňsizlik (a b, a b) görnüşinde ýazylýar.
3-nji mysal. 4,6749 we 4,6751 onluk droblary deňeşdireliň. Berlen onluk droblarda birlikler, ondan birler, ýüzden birler
razrýadlardaky sifrler gabat gelýär, müňden birler razrýadynda birinji onluk drobda 4, ikinjide bolsa 5 ýazylypdyr. 5 4 bolanlygy üçin, 4,6751 4,6749.
4-nji mysal. –12 we –19 otrisatel sanlary deňeşdireliň.
–12-niň moduly –19-yň modulyndan kiçi. Diýmek, –12 san –19-dan uludyr, ýagny –12 –19.
Sanlary deňeşdirmegiň garalyp geçilen usullarynyň ählisini hem öz içine alýan usul bar. Ol usul sanlaryň tapawudyny düzmekden we tapawudyň položitel sandygyny, otrisatel sandygyny ýa-da nola deňdigini anyklamakdan ybaratdyr.
Kesgitleme.
Eger a – b 0 bolsa, onda a b;
Eger a – b a b;
Eger a – b = 0 bolsa, onda a = b.
Eger a – b tapawut položitel sana ýa-da nola deň bolsa (otrisatel bolmasa), onda a ≥ b (okalyşy: a san b-den uludyr ýa-da a san b sana deňdir; a san b sandan kiçi däldir).
Eger a – b tapawut otrisatel sana ýa-da nola deň bolsa (položitel bolmasa), onda a ≤ b (okalyşy: a san b-den kiçidir ýa-da a san b sana deňdir; a san b-den uly däldir).
1-nji häsiýet. Eger a b bolsa, onda b a we tersine, eger a b bolsa, onda b a.
Bu häsiýet san göni çyzygynda gowy görünýär:
E![]() ger a koordinataly nokat san göni çyzygynda b koordinataly nokatdan sagda ýatan bolsa, onda b koordinataly nokat a koordinataly nokatdan çepde ýatýar we tersine (9njy surat).
ger a koordinataly nokat san göni çyzygynda b koordinataly nokatdan sagda ýatan bolsa, onda b koordinataly nokat a koordinataly nokatdan çepde ýatýar we tersine (9njy surat).
2-nji häsiýet. Eger a b we b c bolsa, onda a c.
H![]() akykatdan-da, eger san göni çyzygynda a koordinataly nokat b koordinataly nokatdan sagda ýatýan bolsa, b koordinataly nokat bolsa c koordinataly nokatdan sagda ýatýan bolsa, onda a koordinataly nokat c koordinataly nokatdan sagda ýatar
akykatdan-da, eger san göni çyzygynda a koordinataly nokat b koordinataly nokatdan sagda ýatýan bolsa, b koordinataly nokat bolsa c koordinataly nokatdan sagda ýatýan bolsa, onda a koordinataly nokat c koordinataly nokatdan sagda ýatar
(10njy surat).
5. Täze temany berkitmek:
505. 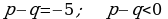 onda
onda 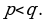
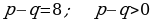 onda
onda 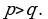
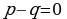 onda
onda 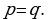
508. b) 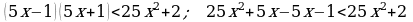
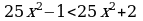 deňlik dogry.
deňlik dogry.
ç) 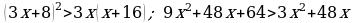 ;
; 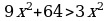 , deňlik dogry.
, deňlik dogry.
6. Öý işini tabşyrmak:
1. Sanlary deňeşdirmegiň nähili usullaryny bilýärsiňiz?
2. a ≥ b we a ≤ b ýazgylar nähili okalýar?
3. Deňsizlikleriň nähili häsiýetleri bar?
4. 4-nji häsiýet bölmek üçin dogrumy?
7. Sapagy jemlemek we okuwçylaryň bilimlerini bahalandyrmak:
Höweslendiriji bahalary goýmak we delillendirmek Okuwçylary delillendirip bahalandyrmak.
Ýazan mugallym: M.Işankulyýew
Bellik:_______________________________________________________________
Barlan: Müdiriň okuw işleri baradaky orunbasary ____________________________












