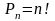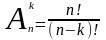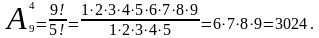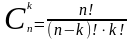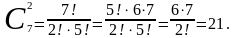832, 26.03.2020 "Решение задач на подсчет числа перестановок, размещений, сочетаний".

Основные понятия комбинаторики: перестановки, сочетания и размещения.

Основная часть

Определение:Комбинаторика – это раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов.

Слово «комбинаторика» происходит от латинского слова «combinare», что в переводе на русский означает – «сочетать», «соединять». Комбинаторные задачи возникли и в связи с такими играми, как шашки, шахматы, домино, карты, кости и т.д. 

Термин "комбинаторика" был введён знаменитым Готфридом Вильгельмом Лейбницем, - всемирно известным немецким учёным.

Комбинаторные задачи делятся на:задачи на перестановки, задачи на размещение, задачи на сочетание

Определение:Факториал – это произведение всех натуральных чисел от 1 до n.

Обозначение: n! = 1 · 2 · 3 · ... · n.Читается: «эн факториал».

Пример: 4! = 1 · 2 · 3 · 4 = 24.

Кроме того: 0! = 1.

Задачи на перестановки

Сколькими способами можно расставить 3 различные книги на книжной полке?

Это задача на перестановки.

Решение: Выбираем одну из 3-х книг и ставим на первое место. Это можно сделать 3-мя способами.

Вторую книгу мы можем выбрать из 2-х оставшихся двумя способами, получаем 3·2 способов.

Третью книгу мы можем выбрать 1 способом.

Получится 3·2·1=6 способов.

Ответ: 6.

Определение:Перестановками из n элементов называются комбинации из n элементов, отличающиеся друг от друга только порядком расположения в них элементов.

Формула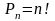

Типичная смысловая нагрузка: «Сколькими способами можно переставить n объектов?»

Пример 1. Сколькими способами можно расставить 8 участников финального забега на восьми беговых дорожках?

Решение: P₈= 8!=1 ∙ 2 ∙ 3 ∙ 4 ∙ 5 ∙ 6 ∙ 7 ∙ 8 = 40320.

Ответ: 40320.

Задача 1. Сколькими способами можно составить расписание на один день, если в этот день предусмотрено 6 уроков по 6 разным предметам?

Задача 2. Сколькими различными способами можно разместить на скамейке 10 человек?
Задача 3. Сколько слов можно получить, переставляя буквы в слове Гора?

Задача 4*. Сколько различных шестизначных чисел, кратных 5, можно составить из цифр 1, 2, 3, 4, 5, 6 при условии, что цифры в числе не повторяются?

Задачи на размещения

Имеется 5 книг и одна полка, такая что на ней вмещается лишь 3 книги.

Сколькими способами можно расставить на полке 3 книги?

Это задача на размещение.

Решение: Выбираем одну из 5-ти книг и ставим на первое место на полке. Это можно сделать 5-ю способами.

Вторую книгу мы можем выбрать 4-мя способами и поставить рядом с одной из 5-ти возможных первых.

Таких пар может быть 5·4.

Третью книгу мы можем выбрать 3-мя способами.

Получится 5·4·3 разнообразных троек. Значит всего способов разместить 3 книги из 5-ти 5·4·3 = 60.

Ответ: 60.

Определение: Размещением из n элементов по k (k≤n) называется любое множество, состоящее из k элементов, взятых в определённом порядке из данных n элементов.

Формула: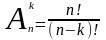

Типичная смысловая нагрузка: «Сколькими способами можно выбрать k объектов и в каждой выборке переставить их местами?»

Пример 1. Учащиеся второго класса изучают 9 предметов. Сколькими способами можно составить расписание на один день, чтобы в нём было 4 различных предмета?

Решение: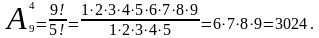

Ответ: 3024.

Задача 1. Сколько трехзначных чисел можно составить из цифр 2, 4, 6, 7, 9?

Задача 2. В соревнованиях высшей лиги по футболу участвуют 18 команд. Борьба идет за золотые, серебряные и бронзовые медали. Сколькими способами могут быть распределены медали между командами?

Задача 3. Сколькими способами можно опустить 5 писем в 11 почтовых ящиков, если в каждый ящик опускают не более одного письма?

Задача 4. Боря, Дима и Володя сели играть в карты. Сколькими способами им можно сдать по одной карте? (колода содержит 36 карт)

Задача 5. В пассажирском поезде 9 вагонов. Сколькими способами можно рассадить в поезде 4 человека, при условии, что все они должны ехать в различных вагонах?

Решение:

Задачи на сочетания

Сколькими способами можно расставить 3 тома на книжной полке, если выбирать их из имеющихся в наличии внешне неразличимых 5 книг?

Это задача на сочетания.

Решение: Книги внешне неразличимы. Но они различаются, и существенно! Эти книги разные по содержанию. Возникает ситуация, когда важен состав элементов выборки, но несущественен порядок их расположения.

123 124 125 134 135 145

234 235 245

345

Ответ: 10.

Определение: Сочетанием из n элементов по k (kn) называется любое множество, составленное из k элементов, выбранных из данных n элементов (не имеет значения, в каком порядке указаны элементы).

Формула: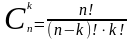

Типичная смысловая нагрузка: «Сколькими способами можно выбрать k объектов из n?»

Пример 1. В классе 7 человек успешно занимаются математикой. Сколькими способами можно выбрать из них двоих для участия в математической олимпиаде?

Решение: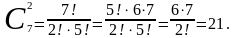

Ответ: 21.

Задача 1. На тренировках занимаются 12 баскетболистов. Сколько может быть организовано тренером разных стартовых пятерок?

Задача 2. В ящике находится 15 деталей. Сколькими способами можно взять 4 детали?

Задача 3. Сколькими способами из колоды в 36 карт можно выбрать 3 карты?

Задача 4*. Для участия в команде тренер отбирает 5 мальчиков из 10. Сколькими способами он может сформировать команду, если 2 определенных мальчика должны войти в команду?

Задача 5*. В шахматном турнире принимали участие 15 шахматистов, причем каждый из них сыграл только одну партию с каждым из остальных. Сколько всего партий было сыграно в этом турнире?

Задача 6*. Сколько различных дробей можно составить из чисел 3, 5, 7, 11, 13, 17 так, чтобы в каждую дробь входили 2 различных числа? Сколько среди них будет правильных дробей?