Россия, Республика Крым
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 13.05.2025 10:10
Перелыгина Елена Алексеевна
заместитель директора по УВР, учитель математики и физики
60 лет
5 534
9 611 
Местоположение
Специализация
"Аксиомы стереометрии и их свойства" (урок по геометрии 10 класс).
Категория:
Математика
01.06.2017 22:56
Просмотр содержимого документа
«"Аксиомы стереометрии и их свойства" (урок по геометрии 10 класс).»
10 класс геометрия
Аксиомы стереометрии
1. Аксиомы стереометрии и их следствия.
6/1/17
Цели:
- Изучить аксиомы стереометрии:
- о взаимном расположении точек,
- о взаимном расположении прямых,
- о взаимном расположении плоскостей
в пространстве.
- Изучить некоторые следствия из аксиом стереометрии.
- Показать применение аксиом к решению задач.
6/1/17
Изучение нового материала.
Планиметрия
Стереометрия
Изучает свойства геометрических фигур на плоскости
Изучает свойства фигур в пространстве
Слово «стереометрия» происходит от греческих слов «стереос» объемный, пространственный, «метрео» – мерить
В переводе с греческого слово «геометрия» означает «землемерие»
«гео» – по-гречески земля, «метрео» – мерить
Л.С. Атанасян. Геометрия 10-11. п. 1.
6/1/17
3
3
Изучение нового материала.
Планиметрия
Стереометрия
Основные фигуры : точка, прямая, плоскость
Основные фигуры: точка, прямая
Наряду с этими фигурами мы будем рассматривать геометрические тела и их поверхности.
Например, многогранники. Куб, параллелепипед, призма, пирамида.
Тела вращения.
Шар, сфера, цилиндр, конус.
Другие фигуры : отрезок, луч, треугольник, квадрат, ромб, параллелограмм, трапеция, прямоугольник, выпуклые и невыпуклые n-угольники, круг, окружность, дуга и др.
6/1/17
3
Для обозначение точек используем прописные латинские буквы
F
D
A
Для обозначение прямых используем строчные латинские буквы
f
d
h
Или обозначаем прямую двумя прописными латинскими буквами.
N
S
6/1/17
5
Плоскости будем обозначать греческими буквами.
На рисунках плоскости обозначаются в виде параллелограммов. Плоскость как геометрическую фигуру следует представлять себе простирающейся неограниченно во все стороны.
6/1/17
5
D
C
C
A
B
5
6/1/17
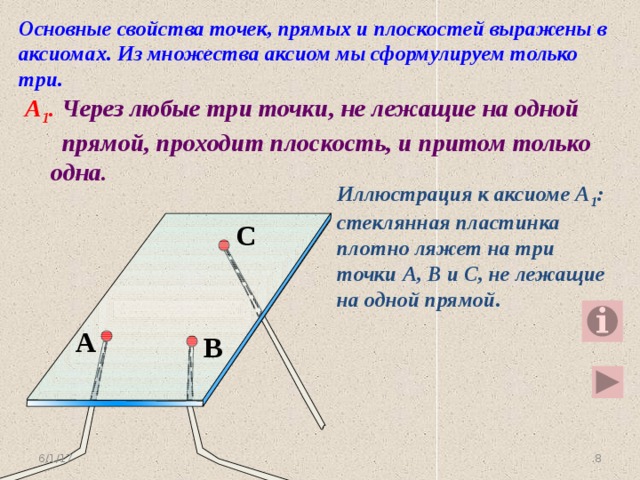
Основные свойства точек, прямых и плоскостей выражены в аксиомах. Из множества аксиом мы сформулируем только три.
А 1 . Через любые три точки, не лежащие на одной
прямой, проходит плоскость, и притом только одна.
Иллюстрация к аксиоме А 1 : стеклянная пластинка плотно ляжет на три точки А, В и С, не лежащие на одной прямой.
C
На кнопку «i» можно нажать несколько раз.
A
B
6/1/17
7
7
А 2 . Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.
B
a
A
Геометрия: Учеб. Для 10-11 кл. общеобразова. учреждений / Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев и др. – 9-е изд., с изм. – М.: Просвящение, 2000. – 206 с.:ил. – ISBN 5-09-008612-5.
6/1/17
7
7
Из аксиомы А 2 следует, что если прямая не лежит в данной плоскости, то она имеет с ней не более одной общей точки. Если прямая и плоскость имеют только одну общую точку, то говорят, что они пересекаются.
a
N
6/1/17
10
10
А 3 . Если две плоскости имеют общую точку, то они
имеют общую прямую, на которой лежат все общие
точки этих плоскостей.
a
Геометрия: Учеб. Для 10-11 кл. общеобразова. учреждений / Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев и др. – 9-е изд., с изм. – М.: Просвящение, 2000. – 206 с.:ил. – ISBN 5-09-008612-5.
В этом случае говорят, что плоскости пересекаются по прямой.
6/1/17
10
10
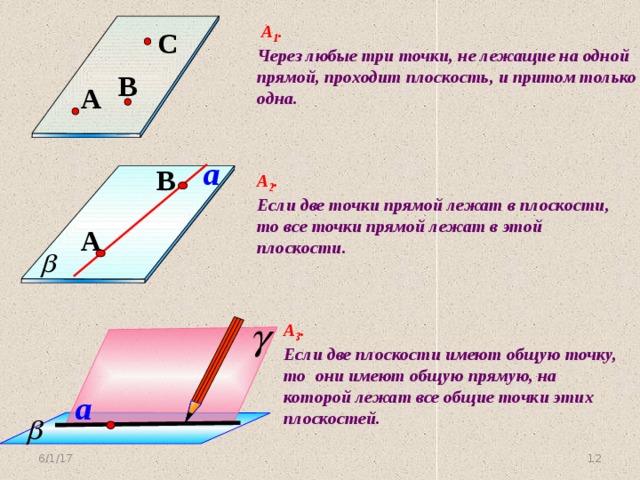
А 1 .
Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
C
B
A
a
B
А 2 .
Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.
A
А 3 .
Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
a
12
6/1/17
Закрепление изученного материала.
Назовите плоскости, в которых лежат прямые
РЕ
МК
DB
AB
EC
D
K
P
M
C
Л.С. Атанасян. Геометрия 10-11. № 8. На кнопку «i» нажмите несколько раз.
A
E
B
6/1/17
12
12
Закрепление изученного материала.
Назовите
точки пересечения прямой DK с плоскостью АВС,
прямой СЕ с плоскостью АDB.
D
K
P
M
C
Л.С. Атанасян. Геометрия 10-11. № 8.
A
E
B
6/1/17
12
12
Закрепление изученного материала.
Назовите точки, лежащие в плоскостях АDB и DBC
D
K
P
M
C
Л.С. Атанасян. Геометрия 10-11. № 8.
A
E
B
6/1/17
12
12
Закрепление изученного материала.
Назовите прямые по которым пересекаются плоскости
АВС и DCB
ABD и CDA
PDC и ABC
D
K
P
M
C
Л.С. Атанасян. Геометрия 10-11. № 8.
A
E
B
6/1/17
12
12
Ответить на вопросы:
- Назвать аксиомы стереометрии:
- о взаимном расположении точек,
- о взаимном расположении прямых,
- о взаимном расположении плоскостей
в пространстве.
6/1/17
12
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
