Понятие стереометрии аксиомы.

Дата проведения:

Преподаватель: Касымова У.Ш.

Группа:

Тема урока: Понятие стереометрии аксиомы.

Цели урока:

Образовательная:

1) ознакомить учащихся с содержанием курса стереометрии;

2) изучить аксиомы о взаимном расположении точек, прямых и плоскостей в пространстве;

Развивающая: развивать логическое мышление.

Воспитательная: развивать такие личностные качества, как самостоятельность, целеустремленность.

Тип урока: комбинированный

Методы обучения: объяснительно-иллюстративный, дедуктивно-репродуктивный.

Литература:

Геометрия 10-11 класс Л. С. Атанасян и др. М.: Просвещение, 2003

Ход урока

1. Организационный момент.

Подготовка учащихся к уроку, проверка Д/з

2. Изучение нового материала.

Учитель знакомит с понятием стереометрии: С 7 класса вы начали знакомиться со школьным курсом геометрии.

Учитель: Что такое геометрия? (Геометрия — наука о свойствах геометрических фигур. Слово «геометрия» — греческое, в переводе — «землемерие». Такое название связано с применением геометрии для измерений на местности.) В 7—9 классах вы изучали первый раздел геометрии — планиметрию.

Учитель: что такое планиметрия? (Планиметрия — раздел геометрии, в котором изучаются свойства фигур на плоскости.)

Вспомним основные понятия планиметрии (см. плакат 1) (точка, прямая: обозначение, изображение).

Не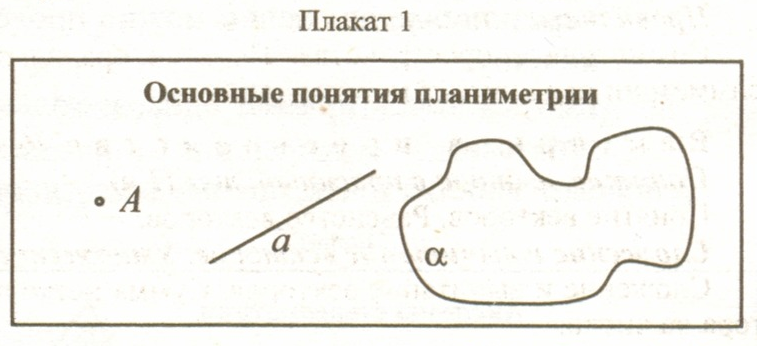 обходимо отметить, что эти понятия не определяемы, они принимаются интуитивно.

Сегодня мы приступим к изучению нового раздела геометрии — стереометрии.

Определение учащиеся записывают в тетрадь под руководством учителя Стереометрия — раздел геометрии, в котором изучается свойства фигур в пространстве.

Основные фигуры в пространстве: точка, прямая и плоскость.

Для обозначения точек используем прописные латинские буквы A, D, F и т. д.

Для обозначения прямых используем строчные латинские буквы f, d, h и т.д.. Или обозначаем прямую двумя прописными латинскими буквами SN.

Представление плоскости дает гладкая поверхность стены, стола.

Уч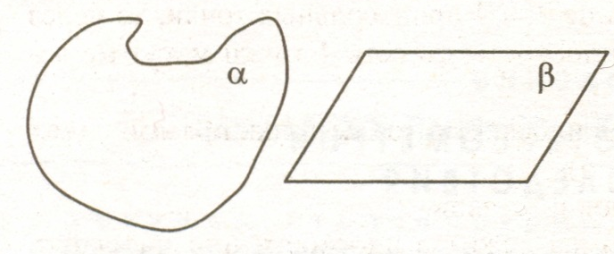 итель изображает на доске, учащиеся в тетради.

Плоскости обозначаются греческими буквами α, β, γ‚ и т.д. Плоскость как геометрическую фигуру следует представлять себе простирающейся во все стороны, не ограниченной.

Необходимо отметить, что об этих фигурах мы имеем наглядное представление, но определения этих фигур в геометрии не даются. Их свойства выражены в аксиомах. С ними мы познакомимся немного позже.

Наряду с точкой, прямой и плоскостью в стереометрии рассматривают геометрические тела, изучают их свойства, вычисляют их площади и объемы. Представление о геометрических телах дают окружающие нас предметы.

Учитель показывает модели и приводит примеры из окружающей действительности (см. плакат 2).

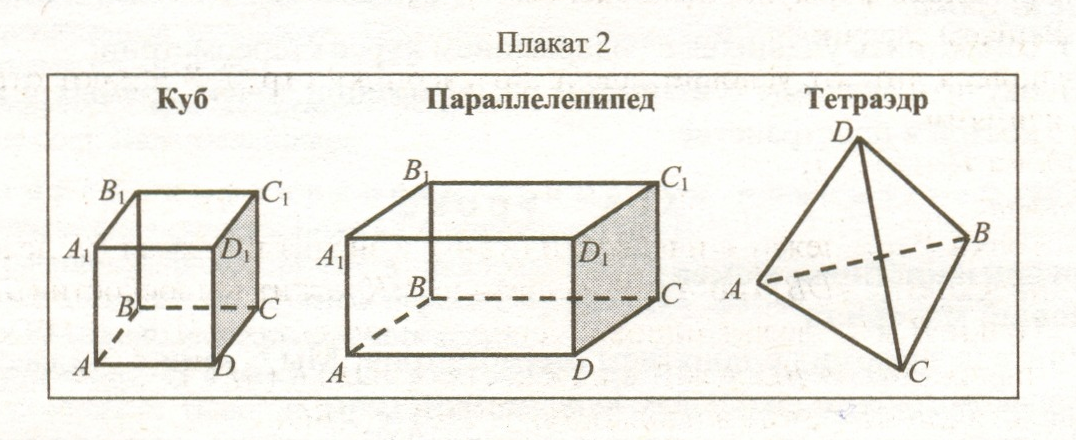
Учащиеся изображают в тетрадях куб и выделяют другим цветом некоторые элементы (точки, отрезки), например: точка А, отрезок ВС.

Теперь рассмотрим аксиомы стереометрии.

Учитель:

• 1) Что такое аксиома? (Аксиома — это первоначальные факты геометрии, которые принимаются без доказательств и позволяют вывести из них дальнейшие факты этой науки.)

2) Какие аксиомы планиметрии вы знаете?

— через любые две точки можно провести прямую, и притом только одну.

— из трех точек прямой одна, и только одна, лежит между двумя другими.

Основные свойства точек, прямых и плоскостей, касающиеся их взаимного расположения, выражены в аксиомах:

А₁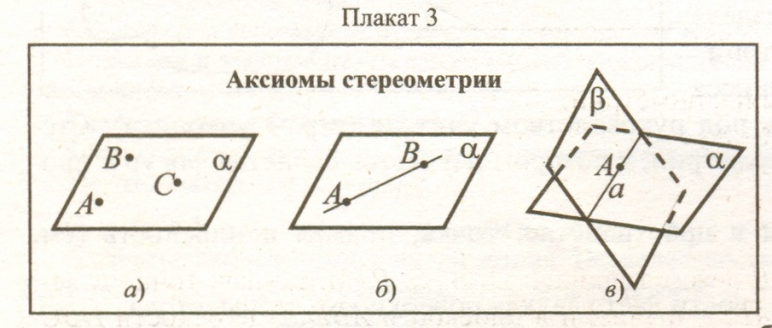 . Через любые 3 точки, не лежащие на одной прямой, проходит плоскость и притом только одна.

Учащиеся под руководством учителя выписывают в тетрадь из учебника (стр. 5) аксиому А₁. делают рисунок.

Важно отметить, что если взять не 3, а 4 произвольные точки, то через них может не проходить ни одна плоскость, то есть 4 точки могут не лежать в одной плоскости.

А₂. Если 2 точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.

Ученики делают запись и рисунок в тетрадь.

В этом случае говорят, что прямая лежит в плоскости или плоскость проходит через прямую. Из аксиомы А₂ следует, что если прямая не лежит в данной плоскости, то она имеет с ней не более одной общей точки. Если прямая и плоскость имеют только одну общую точку, то говорят, что они пересекаются.

А₃. Если 2 плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.

Говорят, плоскости пересекаются по прямой. Ученики делают запись на рисунок в тетрадь.

3. Закрепление изученного материала

1. Прочитать формулировки аксиом А₁—А₃.

2. Решаем задачи:

Учащиеся читают условие задачи по учебнику стр. 7—8 и дают ответ с объяснениями

Задача 1

Ответ:

а) Точки Р и Е лежат в плоскости (АDВ), а значит и прямая РЕ лежит в плоскости (АDВ) (по А₂). Аналогично МК лежит в плоскости (ВDС). Точки В и D лежат одновременно в плоскостях (АDВ) и (ВDС), а значит прямая ВD лежит в плоскостях (АDВ) и (АВС).

Аналогично АВ лежит в плоскостях (АDВ) и (АВС).

Точки С и Е лежат одновременно в плоскостях (АВС) и (DЕС), а значит прямая СЕ лежит в этих же плоскостях.

б) Заметим, что точка С лежит на прямой (DК) и в плоскости АВС, а следовательно, DК∩(АВС) в точке С, так как точек пересечения более одной (прямая не лежит в плоскости), то это единственная точка.

Аналогично СЕ пересекается с плоскостью (АDВ) в точке Е.

Задача 2

Ответ: а) В плоскости ADB: A, D, B, P, M, E. (см. №1). В плоскости DBC: D, B, C, M, K.

Задание 3

Ответ: АВС и DCB: BC

ABD и CDA: AD

PDC и ABC: EC

4. Подведение итогов

Мы познакомились с новым разделом геометрии — стереометрией, узнали новые аксиомы и использовали их при решении задач.

Что нового вы узнали на сегодняшнем уроке?

Объявление оценок (с комментариями).

Домашнее задание

Повторить аксиомы планиметрии.

Выучить аксиомы А₁—А₃.

Прочитать пункт 1—2.

Задача 1(в, г)