Алгебра логики, таблицы истинности и анализ логических схем

АЛГЕБРА ЛОГИКИ

Логические выражения и таблицы истинности

Логика

• ЛОГИКА - наука о формах и способах мышления.

Аристотель (384-322 до н.э.). Основоположник формальной логики (понятие, суждение, умозаключение).

Джордж Буль (1815-1864). Создал новую область науки - Математическую логику (Булеву алгебру или Алгебру высказываний).

Клод Шеннон (1916-2001). Его исследования позволили применить алгебру логики в вычислительной технике

Формы мышления

Мышление всегда осуществляется в определённых формах -  понятие, суждение, умозаключение .

Игровой компьютер (англ. gaming computer) – это настольный компьютер , целью которого является повышенная производительность в современных играх, где требуется большая графическая и вычислительная мощность.

• Компьютер с такими параметрами мне нужен.

Формы мышления

ПОНЯТИЕ - форма мышления, фиксирующая основные, существенные признаки объекта, которые отличают его от других объектов. Понятие имеет две стороны: СОДЕРЖАНИЕ и ОБЪЕМ . Содержание понятия составляет совокупность существенных признаков объекта. Чтобы раскрыть содержание понятия, следует найти признаки, необходимые и достаточные для выделения данного объекта из множества других объектов. Например, содержание понятия ПК - устройство для автоматической обработки информации, предназначенное для одного пользователя. Объем понятия определяется совокупностью предметов, на которые оно распространяется. Например, объем понятия "ПК" выражает всю совокупность (сотни млн.) существующих в настоящее время в мире ПК.

Формы мышления

• ВЫСКАЗЫВАНИЕ (СУЖДЕНИЕ)  - форма мышления, в которой что-либо утверждается или отрицается о реальных предметах, их свойствах и отношениях между ними. Высказывание может быть либо ИСТИННО , либо ЛОЖНО . ИСТИННЫМ будет высказывание, в котором связь понятий правильно отражает свойства и отношения реальных вещей. ЛОЖНЫМ высказывание будет в том случае, когда оно не соответствует реальной действительности. В русском языке высказывания выражаются повествовательными предложениями: - Земля вращается вокруг Солнца . - Москва - столица. Не всякое повествовательное предложение является высказыванием: - Без стука не входить! - Откройте учебники. - Ты выучил стихотворение?

Высказывание, состоящее из одного суждения, называется простым . На основании простых высказываний могут быть построены СОСТАВНЫЕ ВЫСКАЗЫВАНИЯ . Например, "процессор является устройством обработки информации и принтер - устройством печати". Истинность или ложность составных высказываний вычисляется с помощью использования алгебры высказываний.

Формы мышления

• УМОЗАКЛЮЧЕНИЕ   - форма мышления, с помощью которой из одного или нескольких суждений (посылок) может быть получено новое суждение (вывод). Умозаключения позволяют на основе известных фактов, выраженных в форме суждений, получать заключение, т.е. новое знание. Например, если имеем суждение - "Все углы треугольника равны", то получим путем доказательства суждение - "Это треугольник равносторонний". Посылками умозаключения по правилам формальной логики могут быть только истинные суждения. Тогда, если умозаключение проводится в соответствии с правилами формальной логики, то оно будет истинным. В противном случае, можно придти к ложному умозаключению.

Алгебра логики

• Алгебра высказываний (математическая логика или булева алгебра, или алгебра логики) была  разработана для того, чтобы можно было определять истинность или ложность составных высказываний, не вникая в их содержание.
• В алгебре логики высказывания обозначают буквами (заглавные буквы латинского алфавита) и называют логическими переменными , которые могут принимать только два значения "истина" (1) и "ложь" (0).
• 0 и 1 называются логическими значениями .

Например, А - "2х2=4" - истина (1) А=1

                   В - "2х2=5" - ложь (0)     В=0

• Простые высказывания называются  переменными , сложные -  логическими функциями.
• Простые высказывания называются  переменными , сложные -  логическими функциями.

Решение логической задачи

УСЛОВИЕ ЗАДАЧИ

Покупатель в каждом из магазинов А, B, C, D сделал по одной покупке и приобрел джойстик, диски, бумагу и картридж, известно, что:

• -  джойстик и картридж купил не в “А”;
• -  в “С” зашел, когда уже купил диски и бумагу;
• -  в “D” не было ни картриджа, ни дисков;
• -  в “В” приехал, когда джойстик уже был куплен, а из  “D” уходил еще без джойстика.

В каком магазине были куплены диски?

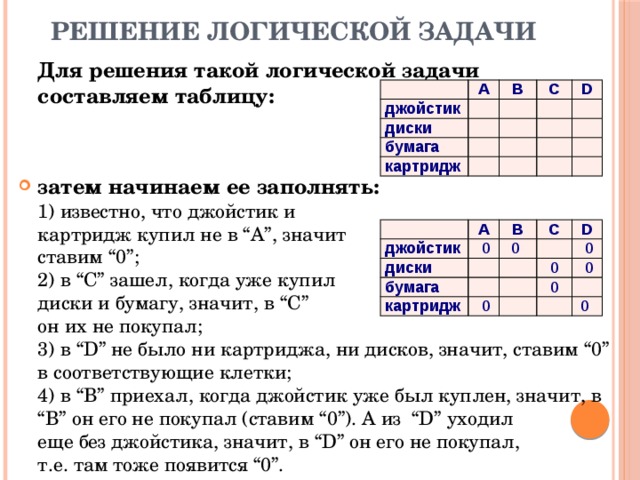
Решение логической задачи

Для решения такой логической задачи составляем таблицу:

• затем начинаем ее заполнять: 1) известно, что джойстик и картридж купил не в “А”, значит ставим “0”; 2) в “С” зашел, когда уже купил диски и бумагу, значит, в “С” он их не покупал; 3) в “D” не было ни картриджа, ни дисков, значит, ставим “0” в соответствующие клетки; 4) в “В” приехал, когда джойстик уже был куплен, значит, в “В” он его не покупал (ставим “0”). А из  “D” уходил еще без джойстика, значит, в “D” он его не покупал, т.е. там тоже появится “0”.

джойстик

A

диски

B

C

бумага

D

картридж

джойстик

A

диски

B

  0

бумага

0 

C

D

картридж

  0

0 

  0

  0

0

0 

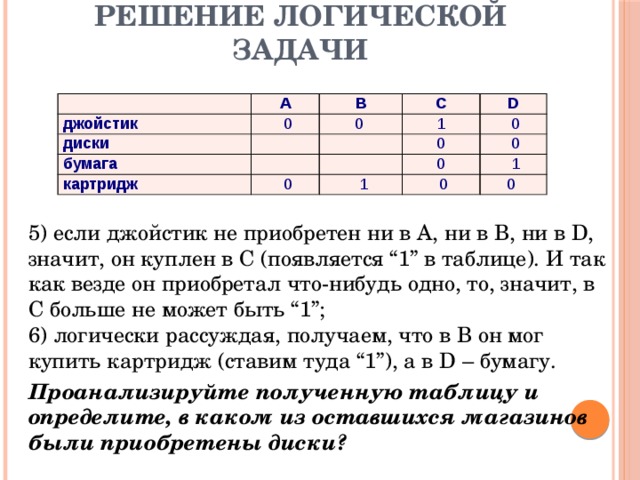
Решение логической задачи

джойстик

A

диски

B

  0

бумага

0 

C

D

картридж

1

0 

  0

  0

  0

0

  1

  1

  0

0 

5) если джойстик не приобретен ни в А, ни в В, ни в D, значит, он куплен в С (появляется “1” в таблице). И так как везде он приобретал что-нибудь одно, то, значит, в С больше не может быть “1”; 6) логически рассуждая, получаем, что в В он мог купить картридж (ставим туда “1”), а в D – бумагу.

Проанализируйте полученную таблицу и определите, в каком из оставшихся магазинов были приобретены диски?

Логические операции

• ЛОГИЧЕСКОЕ УМНОЖЕНИЕ  (КОНЪЮНКЦИЯ ) - объединение 2-х (или нескольких высказываний) в одно с помощью союза "И".  Истинна, если оба высказывания истинны .

Обозначения:  ,  , & , И, AND.

Графическое представление

Таблица истинности:

А

0

В

А&В

0

0

0

1

1

1

0

0

1

0

1

A

B

А&В

Логические операции

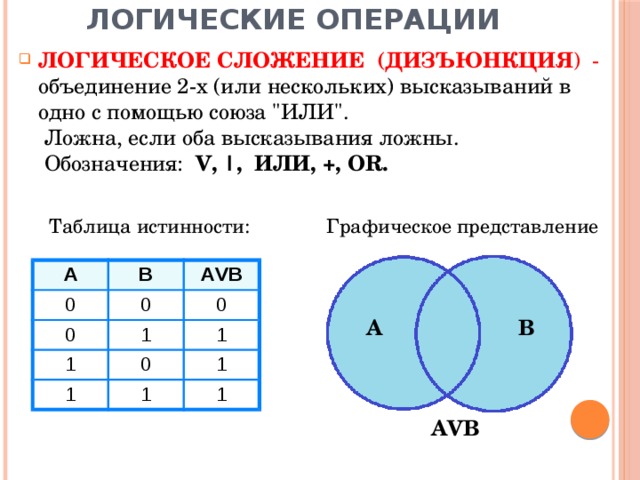
• ЛОГИЧЕСКОЕ СЛОЖЕНИЕ  (ДИЗЪЮНКЦИЯ )  - объединение 2-х (или нескольких) высказываний в одно с помощью союза "ИЛИ". Ложна, если оба высказывания ложны. Обозначения: V, |, ИЛИ, +, OR.

Графическое представление

Таблица истинности:

А

0

В

АVВ

0

0

1

0

1

1

0

1

1

1

1

A

B

АVВ

Логические операции

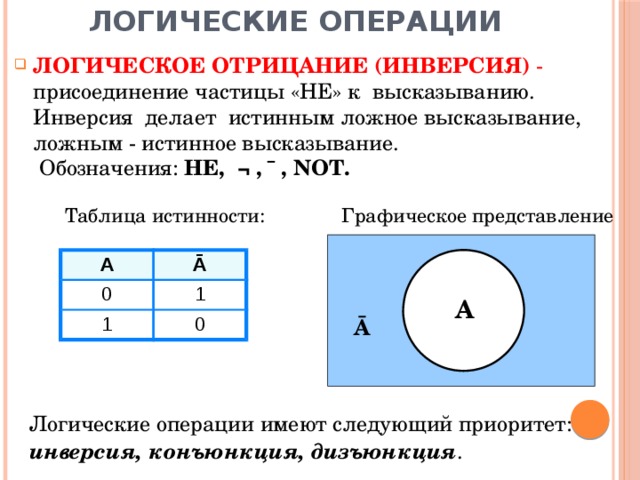
• ЛОГИЧЕСКОЕ ОТРИЦАНИЕ (ИНВЕРСИЯ)  - присоединение частицы «НЕ» к  высказыванию.  Инверсия  делает  истинным ложное высказывание, ложным - истинное высказывание. Обозначения: НЕ, ¬ , ¯ , NOT.

Таблица истинности:

Графическое представление

А

0

Ā

1

1

0

A

Ā

Логические операции имеют следующий приоритет:

инверсия, конъюнкция, дизъюнкция .

ЗАДАНИЕ

1. Девочки  Л ера,  Т аня и  М аша зашли в кафе. Выяснилось, что каждая девочка заказала самое любимое блюдо. Девочки заметили, что они заказали три различных блюда в кафе: борщ, пирожное и овощной салат. Таня сказала, что ей не нравятся супы, т.к. мама их готовит каждый день. Лера предпочитает сладкое и не понимает своих подружек, которые в кафе заказывают первые или вторые блюда. Какие блюда выбрали девочки?

2. Пусть А = «Ане нравится математика», а В = «Ане нравится химия». Выразите следующие формулы на обычном языке:

3. Определите высказывание А V A & B, заполнив таблицу:

A

B

0

A&B

0

0

1

AVA&B

1

1

0

1

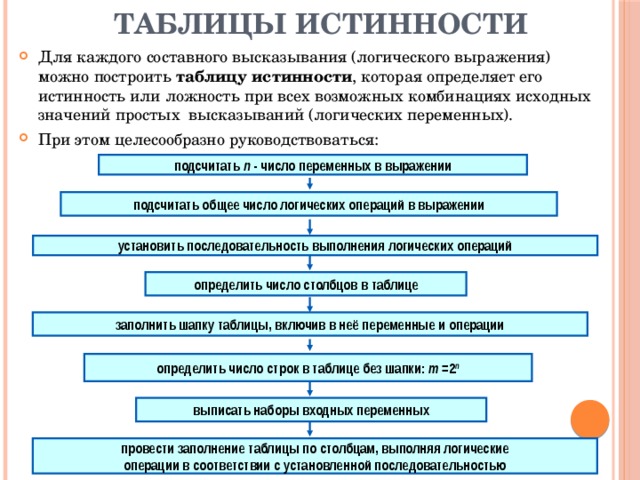
ТАБЛИЦЫ ИСТИННОСТИ

• Для каждого составного высказывания (логического выражения) можно построить таблицу истинности , которая определяет его истинность или ложность при всех возможных комбинациях исходных значений простых  высказываний (логических переменных).
• При этом целесообразно руководствоваться:

подсчитать n - число переменных в выражении

подсчитать общее число логических операций в выражении

установить последовательность выполнения логических операций

определить число столбцов в таблице

заполнить шапку таблицы, включив в неё переменные и операции

определить число строк в таблице без шапки: m =2 n

выписать наборы входных переменных

провести заполнение таблицы по столбцам, выполняя логические

операции в соответствии с установленной последовательностью

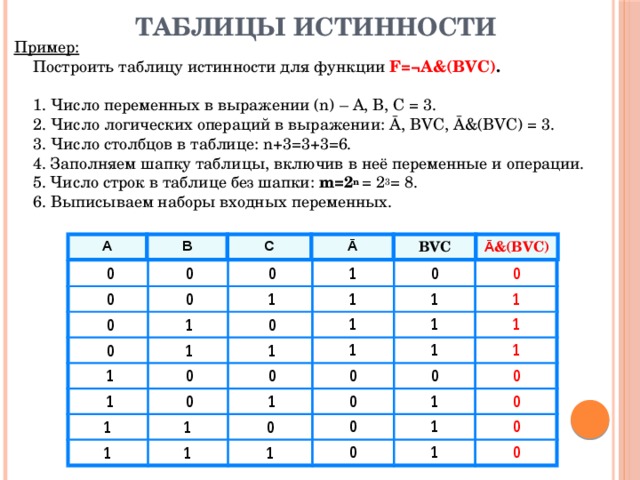
ТАБЛИЦЫ ИСТИННОСТИ

Пример: Построить таблицу истинности для функции F=¬А&(BVC) . 1. Число переменных в выражении (n) – A, B, C = 3. 2. Число логических операций в выражении: Ā, BVC , Ā&(BVC) = 3. 3. Число столбцов в таблице: n+3=3+3=6. 4. Заполняем шапку таблицы, включив в неё переменные и операции. 5. Число строк в таблице без шапки: m=2 n = 2 3 = 8. 6. Выписываем наборы входных переменных.

A

B

С

Ā

BVC

Ā &(BVC)

  0

  0

  0

  0

  0

  0

1

  0

  1

  1

  0

0

  1

1

  1

1

  1

1

  1

  0

0

1

1

  0

  0

1

1

0

1

1

1

1

  1

0

0

0

1

1

1

0

1

0

1

0

0

1

0

0

ОСНОВНЫЕ ЗАКОНЫ ЛОГИКИ

• Закон тождества.   Всякое высказывание тождественно самому себе: А = А
• Закон непротиворечия.   Высказывание не может быть одновременно истинным и ложным. Если высказывание А — истинно, то его отрицание не А должно быть ложным. Следовательно, логическое произведение высказывания и его отрицания должно быть ложно:  A & ¬A = 0
• Закон исключенного третьего . Высказывание может быть либо истинным, либо ложным, третьего не дано. Это означает, что результат логического сложения высказывания и его отрицания всегда принимает значение истина:  A v ¬A = 1
• Законы отрицания.  
• Законы операций с 1 и 0. 0=0; A &1 = A

A V B = Ā & B

A & B = Ā V B

A V 0 = A; A V 1 = 1

A & 0=0; A &1 = A

ПРАВИЛА АЛГЕБРАИЧЕСКИХ ПРЕОБРАЗОВАНИЙ

• Законы Моргана:  ¬(AVB)= ¬А & ¬В

                                  ¬(A&B)= ¬А V ¬В

• Правило коммутативности.   В обычной алгебре слагаемые и множители можно менять местами. В алгебре логики можно менять местами логические переменные при операциях логического умножения и логического сложения : Логическое умножение       Логическое сложение

A&B = B&A                        AVB = BVA

• Правило ассоциативности.   Если в логическом выражении используются только операция логического умножения или только операция логического сложения, то можно пренебрегать скобками или произвольно их расставлять : Логическое умножение        Логическое сложение

(A&B)&C = A&(B&C)       (AVB)VC = AV(BVC)

• Правило дистрибутивности.  В отличие от обычной алгебры, где за скобки можно выносить только общие множители, в алгебре высказываний можно выносить за скобки как общие множители, так и общие слагаемые: Дистрибутивность умножения            Дистрибутивность сложения (A&B) V (A&C) = A&(BVC)             (AVB) & (AVC) = AV(B&C)

пример применения законов логики

• Пусть нам необходимо упростить логическое выражение:

(А&В) V (A&¬В)

• Воспользуемся правилом дистрибутивности и вынесем за скобки  А:

(А & В) V (А &¬В) = А & (В V¬В)

• По закону исключенного третьего В V¬В = 1, следователь­но:

А & (В V ¬B) = А&1 = А.

Решение логической задачи

УСЛОВИЕ: Ученики: Коля, Вася и Серёжа на перемене одни остались в кабинете. Один из них разбил стекло в шкафу. На вопрос, кто разбил стекло, они дали такие ответы:

• Серёжа : 1) Я не разбивал. 2) Вася не разбивал.
• Вася : 3) Серёжа не разбивал. 4) Стекло разбил Коля.
• Коля: 5) Я не разбивал. 6) Стекло разбил Серёжа. Согласно их характеристик, классный руководитель предположил, что:
• один из учеников (отличник), оба раза сказал правду;
• второй (двоечник) оба раза сказал неправду;
• третий (хитрец) один раз сказал правду, а другой раз - неправду. Установите: 1) имена «отличника», «двоечника» и «хитреца». 2) кто из учеников разбил стекло?

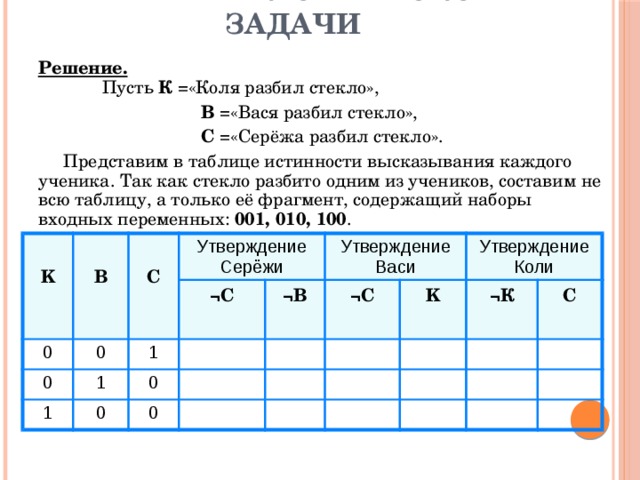
Решение логической задачи

Решение. Пусть К =«Коля разбил стекло»,

В =«Вася разбил стекло»,

С =«Серёжа разбил стекло».

Представим в таблице истинности высказывания каждого ученика. Так как стекло разбито одним из учеников, составим не всю таблицу, а только её фрагмент, содержащий наборы входных переменных: 001, 010, 100 .

K

0

B

0

Утверждение Серёжи

0

C

1

1

1

¬С

0

¬В

Утверждение Васи

0

¬С

0

K

Утверждение Коли

¬К

C

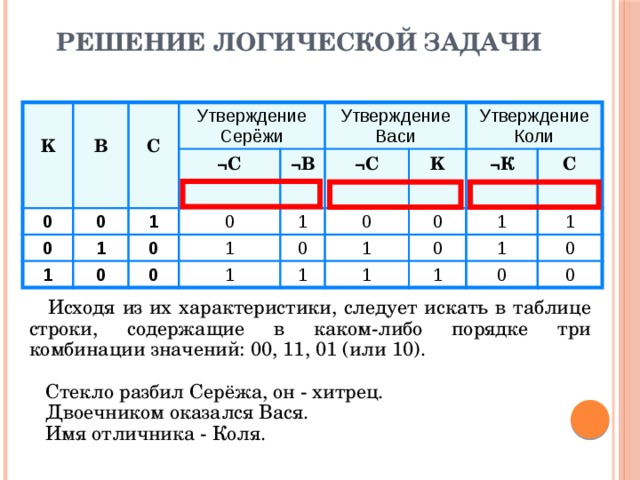
Решение логической задачи

K

B

0

C

Утверждение Серёжи

0

0

1

¬С

1

1

0

0

Утверждение Васи

0

¬В

¬С

0

1

1

Утверждение Коли

1

0

K

0

¬К

1

0

1

1

1

0

C

1

1

1

0

0

0

Исходя из их характеристики, следует искать в таблице строки, содержащие в каком-либо порядке три комбинации значений: 00, 11, 01 (или 10).

Стекло разбил Серёжа, он - хитрец. Двоечником оказался Вася. Имя отличника - Коля.

ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ

• Цифровой сигнал – это сигнал, который может принимать только одно из двух установленных значений 0 или 1.
• Логический элемент – это устройство-преобразователь, который, после обработки двоичных сигналов (высказываний), выдает значение логического отрицания, логической суммы или логического произведения этих сигналов.
• Логическое устройство – это цепочка из логических элементов.
• Функциональная схема  – это  схема соединения логических элементов, реализующая логическую функцию.

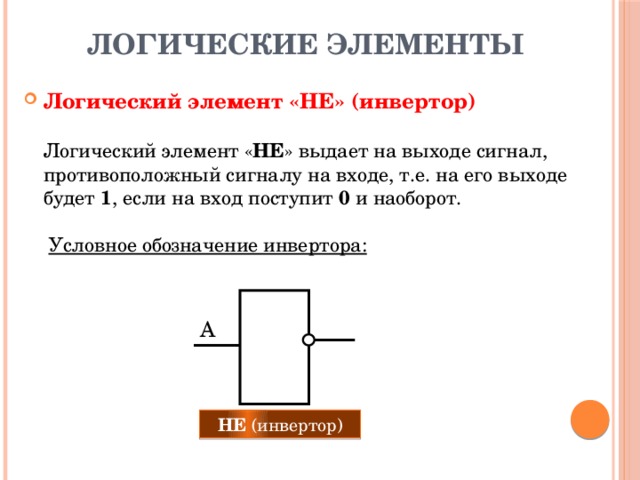
ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ

• Логический элемент «НЕ» (инвертор) Логический элемент « НЕ » выдает на выходе сигнал, противоположный сигналу на входе, т.е. на его выходе будет 1 , если на вход поступит 0 и наоборот.   Условное обозначение инвертора:

А

НЕ (инвертор)

ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ

• Логический элемент «И» (конъюнктор) Логический элемент « И » ( конъюнктор )  выдает на выходе значение логического произведения входных сигналов: на выходе выдает 1 тогда и только тогда, когда на все входы поданы 1. Физическая реализация: последовательное соединение переключателей (елочная гирлянда) . Условное обозначение конъюнктора:

А

&

В

И (конъюнктор)

ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ

• Логический элемент «ИЛИ» (дизъюнктор)

Логический элемент ИЛИ (дизъюнктор) выдает на выходе значение суммы входных сигналов. На выходе выдает 1, если хотя бы на один из входов подается 1.  Физическая реализация: параллельное соединение переключателей (многорожковая люстра). Условное обозначение дизъюнктора:

А

1

В

ИЛИ (дизъюнктор)

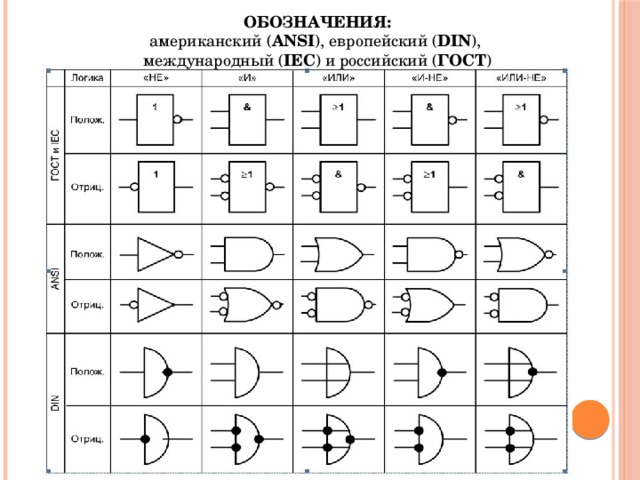
ОБОЗНАЧЕНИЯ:

американский ( ANSI ), европейский ( DIN ),

международный ( IEC ) и российский ( ГОСТ )

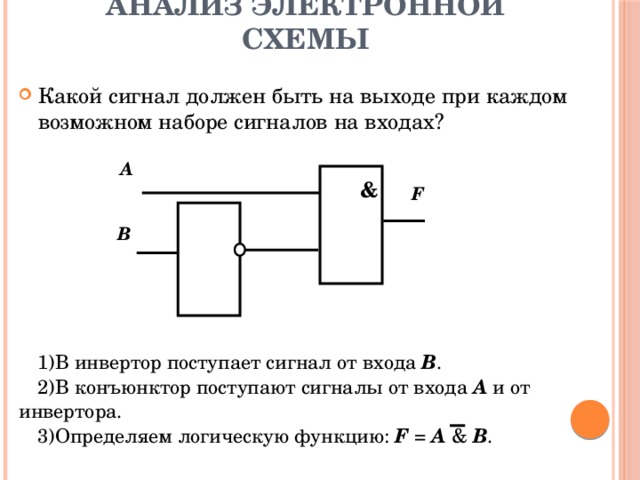
Анализ электронной схемы

• Какой сигнал должен быть на выходе при каждом возможном наборе сигналов на входах?

А

&

F

В

• В инвертор поступает сигнал от входа В .
• В конъюнктор поступают сигналы от входа А и от инвертора.
• Определяем логическую функцию: F = A & B .

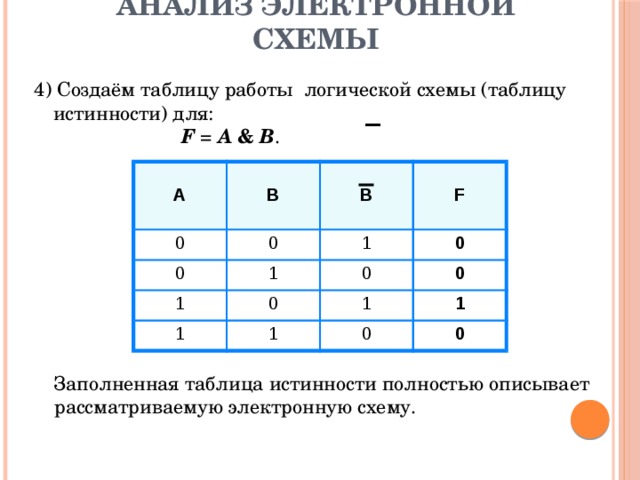
Анализ электронной схемы

4) Создаём таблицу работы логической схемы (таблицу истинности) для: F = A & B .

A

B

0

0

0

B

1

1

1

F

0

0

0

1

0

1

1

1

0

0

Заполненная таблица истинности полностью описывает рассматриваемую электронную схему.

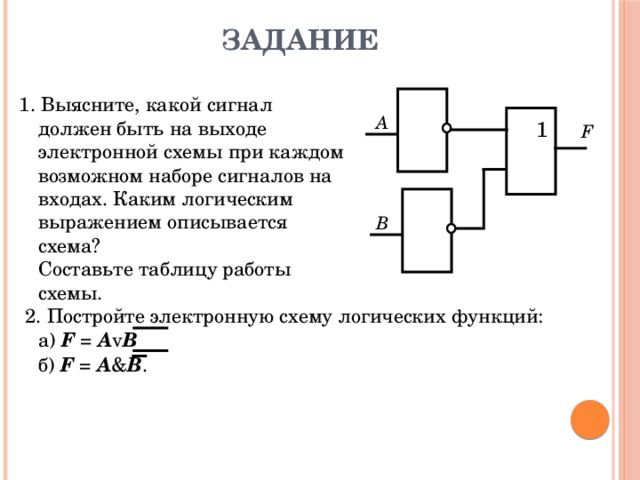
ЗАДАНИЕ

1. Выясните, какой сигнал должен быть на выходе электронной схемы при каждом возможном наборе сигналов на входах. Каким логическим выражением описывается схема? Составьте таблицу работы схемы.

А

1

F

В

2. Постройте электронную схему логических функций: а) F = A v B

б) F = A & B .

ЗАДАЧА 1

Разбирается дело о шпионаже Джона, Брауна и Смита. Известно, что один из них занимался кражей секретной информации. На следствии каждый из подозреваемых сделал два заявления:

• Смит : «Я не делал этого. Браун делал это».
• Джон : «Браун не виновен. Смит делал это».
• Браун : «Я не делал этого. Джон не делал этого».

Суд присяжных установил, что один из них дважды солгал, другой дважды сказал правду, третий один раз солгал, один раз сказал правду.

Кто из подозреваемых должен быть оправдан?

ЗАДАЧА 2 и 3

2. Три девочки – Роза, Маргарита и Анюта представили на конкурс цветоводов корзины выращенных ими роз, маргариток и анютиных глазок. Девочка, вырастившая маргаритки, обратила внимание Розы на то, что ни у одной из девочек имя не совпадает с названием любимых цветов. Какие цветы вырастила каждая из девочек?

3. Три дочери писательницы Жаклин Деманж – Дениз, Амели и Лилиан очень талантливы. Они приобрели известность в разных видах искусств – оперном пении, балете и игре на виолончели. Все они живут в разных городах, поэтому Жаклин часто звонит им в Париж, Рим и Чикаго. Известно что:

- Дениз живёт не в Париже, а Лилиан – не в Риме.

- Парижанка не играет на виолончели.

- Та, кто живёт в Риме, оперная певица.

- Лилиан равнодушна к балету.

Где живёт Амели и какова её профессия?

Париж

0

Рим

Чикаго

Дениз

Пение

0

Балет

Амели

Музыка

Лилиан

0

• F=¬В&(АvCvB)
• F=AvC&DvB

• F= ¬(AvD)&CvB

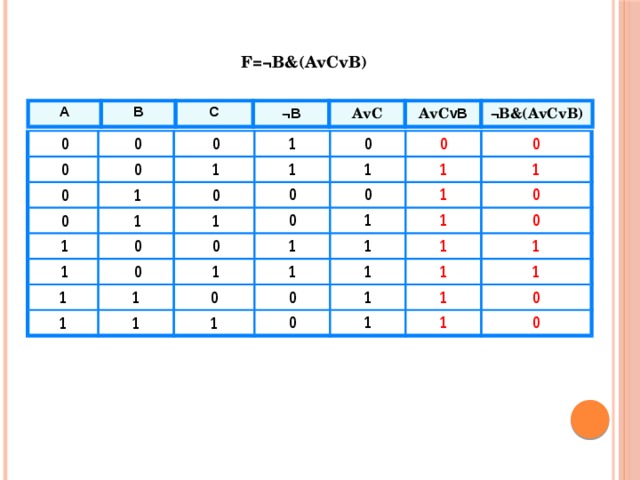
F=¬В&(АvCvB)

A

B

С

¬ B

AvC

AvC vB

¬В&(АvCvB)

  0

  0

  0

  0

  0

  0

1

  1

  0

  1

0

1

  0

  1

  1

0

  0

0

  1

1

  1

1

0

  0

1

  0

0

0

1

1

1

1

1

  1

1

0

1

1

1

0

1

1

0

0

1

1

1

0

1

1

1

1

1

0

1

0

F=AvC&DvB

A

B

0

C

0

0

0

D

0

0

C&D

0

0

0

0

1

AvC&D

0

0

0

1

AvC&DvB

0

0

1

0

0

1

0

0

1

0

1

0

0

0

0

0

1

0

0

1

1

0

1

1

0

1

1

1

0

1

0

0

0

1

0

1

0

1

1

0

0

0

1

0

1

1

0

0

1

0

1

1

1

1

0

1

1

1

1

1

0

0

0

1

1

1

0

1

1

1

1

1

0

0

1

1

1

1

0

1

1

1

1

1

0

1

0

0

1

1

1

1

1

1

1

1

1

F= ¬(AvD)&CvB

A

B

0

C

0

0

0

0

0

D

0

AvD

0

0

0

0

0

1

1

0

¬(AvD)

1

0

1

0

1

¬(AvD)&C

1

1

0

1

0

0

0

0

F

1

0

0

0

1

0

1

0

0

1

1

1

1

0

1

0

1

1

1

0

0

0

1

1

0

0

1

1

0

0

0

0

0

1

1

0

0

0

1

1

1

1

1

1

0

1

1

0

1

1

0

1

1

0

0

1

1

1

1

1

0

0

0

1

1

0

1

0

1

0

0

0

1

1

1

1

0

0

0

1

0

1

0

0

0

1

1

0

0

0

1

0

0

1

1

0

0

1

0

1

A & B = Ā V B

А

0

В

0

A & B

0

0

F

1

1

¬A

1

0

0

1

¬B

1

1

1

0

1

1

F

1

1

1

0

0

0

1

0

1

1

0

0

A V B = Ā & B

А

0

В

A v B

0

0

F

1

0

1

¬A

1

1

0

1

1

1

1

0

¬B

1

1

0

F

1

1

0

0

0

0

0

1

0

0

0

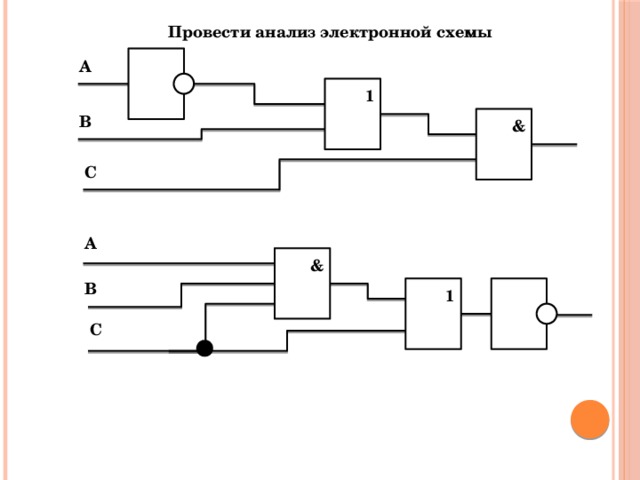
Провести анализ электронной схемы

А

1

В

&

С

А

&

В

1

С

A

B

0

0

0

C

0

D

0

0

0

0

0

0

1

0

0

1

1

0

1

0

1

0

1

0

1

0

0

0

1

1

1

1

1

0

0

1

0

1

1

0

1

0

0

0

0

1

1

1

0

1

1

1

1

1

1

0

1

1

0

0

1

1

1

0

1

1

A

0

B

0

0

1

1

0

1

1

A

0

B

0

C

0

0

0

0

0

1

1

1

0

1

1

0

1

0

1

0

1

1

1

0

1

1