П.2 урок 2-3 Рівень А
Розв’яжіть рівняння:
43. а) 36х = 54; б) 0,04z = 1,4; в) 2y = –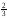 ;
;
г) 1,2х = 0,09; д) 3,86t = 7,913; е)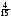 х =
х =  ;
;
є) 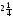 s =
s = 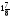 ; ж) 2,5х =
; ж) 2,5х = 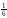 ; з)
; з) 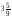 y = 0,6.
y = 0,6.
44. а) 5х 3 = 17; б) 7х + 32 = 12х + 25; в) 4 3y = 6y + 22;
г) 4,5z + 1 = 7z + 2,5; д) 1,2m 2 = m 0,9; е) 1,74х + 7,92 = 1,08х;
є) 4y + 1 = 1 + 4y; ж) 0,77х = 1,65 + 1,1х; з) –16,8х 3 = 6х + 2,7.
45. а) 56х = 196; б) 8х = –8 + 12х; в) 1,15 3z = 2,5;
г) 2y 18 = 3y + 67; д) 6х + 2 = 20х 5; е) 4,5х + 1 = 2 + 4,5х;
є) 8 1,2z = -6z + 152; ж) 4,02t 1 = 1,52t; з) 1,7х + 2,04 = 6,8х.
46. а) 6(х 2) = 2х; б) 3(2х + 1) = 7х; в) 1 (3х + 1) = 2х;
г) 2(2х 4) = 3; д) 2(х + 5) = 2(х 4); е) 3(10 2х) = 6х 30.
47. а) 8х 7 = 3(х – 4); б) –(3х + 1) = 3(3 – х); в) 6х – 2 = 2(1 3х).
Рівень Б
Розв’яжіть рівняння:
48. а) 2(х 11) 5(5 2х) = –23;
б) 8(3х + 4) + 14(3 + 2х) = 4 + 2х;
в) 5(4х + 3) + 3х = 12(х 3); г) 0,5х = 0,1(2х 5) + 1,7.
49. а) 3,5(х 3) 0,7(7 х) = –7; б) 0,4(2х 7) + 1,2(3х + 0,7) = 1,6х;
в) 5(4(х + 1) 9х) = 25(х + 1); г) 0,8(2,2(х 1) 1) 1,4х = 0,4.
50. а) 5(3х 6) + 4(3 2х) = 5х 8; б) 9(х 3) 4(7 3х) 5 = –3х;
в) 0,3(8 4х) = 0,6(х 3) + 0,9; г) 2(0,9х + 1,4) + 1,4(1,5 + х) = х;
д) 40(5х 8(х 1)) = 160(х + 9); е) 12 + 3(2(х 1) 4) = 6(х + 1).
51. Знайдіть значення x, для яких значення виразів 2х 3 і 3 + 7х дорівнюють одне одному.
52. Знайдіть значення x, для яких значення виразу 25х 30 на 5 менше від значення виразу 15х + 15.
53. Знайдіть значення x, для яких значення виразу 4х + 6 у 6 разів більше від значення виразу 6х 15.
Розв’яжіть рівняння:
54. а) 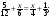 б)
б) 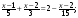
в)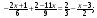 г)
г) 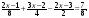
55. а) 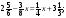 б)
б) 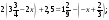
в) 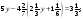 г)
г) 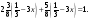
56. а) 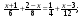 б)
б) 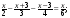
в) 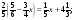 г)
г) 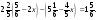
57. а) x = 5; б) x = –6; в) x = 0;
г) 2x – 7 = 11; д) 15 – 4x = 5; е) 7x – 2 = 0.
58. а) x + 3 = 7; б) 3x = 6; в) x + 8 = 3.
59. а) 3x = 12; б) x – 3 = 8; в) x + 2 = –2;
г) x – 7 = 0; д) 2x – 1 = 5; е) 5 – x = –11.
Рівень В
Розв’яжіть рівняння:
60. а) 200(2(2(х 1) 1) 1) = 600;
б) 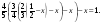
61. а) |2(х 3) (x + 4)| = 2; б) |5х 4(2x + 3)| = 6;
в) 2(|х| 3) 4(2|х| + 9) = 48; г) |2х 1| 4(1 |2х 1|) = 6.
62. а) 3x + x = 20; б) 5x + x = 12; в) x + x = 8;
г) x – x = 12; д) x + x = 0; е) x – x = 0.
63. а) x + x2 = 0; б) x2 + x = –7; в) x + 2x + 4 = 0.
64. У рівнянні аx = 4389 коефіцієнт а є трицифровим числом виду **1. Розв’яжіть це рівняння, якщо відомо, що його коренем є натуральне
число.
Вправи для повторення
65. Обчисліть:
а) 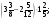 б)
б) 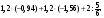
66. З міст А і В одночасно назустріч один одному виїхали два автомобілі й зустрілися через 1,5 год. Швидкість одного автомобіля дорівнює а км/год, а іншого b км/год. Запишіть у вигляді виразу відстань між містами.
67. Легковий автомобіль наздоганяє вантажний. Швидкість легкового автомобіля дорівнює а км/год, а вантажного b км/год. Запишіть у вигляді виразу відстань між автомобілями за 0,2 год до зустрічі.
68. Швидкість катера у стоячій воді (ще кажуть: власна швидкість катера) дорівнює а км/год, а швидкість течії річки — b км/год. Запишіть у вигляді виразу відстань, яку пропливе катер, рухаючись 2 год за течією річки і 3 год проти течії.
69. З кошика взяли 3 яблука, потім — третину решти яблук і ще 3 яблука. Після цього в кошику залишилася половина початкової кількості яблук. Скільки яблук було в кошику спочатку?





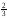 ;
;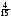 х =
х =  ;
;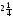 s =
s = 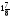 ; ж) 2,5х =
; ж) 2,5х = 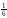 ; з)
; з) 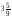 y = 0,6.
y = 0,6.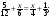 б)
б) 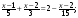
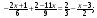 г)
г) 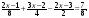
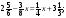 б)
б) 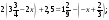
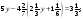 г)
г) 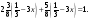
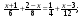 б)
б) 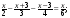
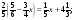 г)
г) 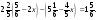
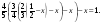
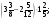 б)
б)