Просмотр содержимого документа
«Алгебра жана геометрия»
Лекция №3
Тема: Чыныгы сандар, алардын үстүнөн жүргүзүлүүчү амалдар.
Рационалдык сандар, алардын үстүнөн жүргүзүлүүчү амалдар.
Чыныгы сандардын түзүлүшү, касиеттери, арифметикасы.
Аныктама. 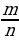 көрүнүшүндөгү сандар рационалдык сандар деп аталат, мында m саны бүтүн сан, ал эми n саны натуралдык сан. Мисалы,
көрүнүшүндөгү сандар рационалдык сандар деп аталат, мында m саны бүтүн сан, ал эми n саны натуралдык сан. Мисалы, 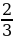 ,
, 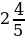 ,
, 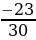 ж. б. сандар. Рационалдык сандардын көптүгү Q тамгасы менен белгиленет жана жалпы түрдө төмөнкүдөй белгиленет: Q
ж. б. сандар. Рационалдык сандардын көптүгү Q тамгасы менен белгиленет жана жалпы түрдө төмөнкүдөй белгиленет: Q  {
{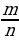
 Q |
Q | 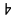 m
m Z,
Z, 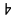 n
n N}.
N}.
Рационалдык сандардын үстүндө кошуу, кемитүү, көбөйтүү жана бөлүү амалдары аткарылат, бул амалдар ар дайым аткарылат, бир гана эч бир бүтүн санды 0 гө бөлүүгө болбойт.
Аныктама. 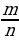 көрүнүшүнө келбеген сандар иррационалдык сандар деп аталат, мында m саны бүтүн сан, ал эми n саны натуралдык сан. Мисалы,
көрүнүшүнө келбеген сандар иррационалдык сандар деп аталат, мында m саны бүтүн сан, ал эми n саны натуралдык сан. Мисалы, 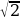 ,
, 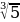 , e, π, sin
, e, π, sin 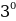 , log23 ж. б. Иррационалдык сандардын көптүгү I тамгасы менен белгиленет.
, log23 ж. б. Иррационалдык сандардын көптүгү I тамгасы менен белгиленет.
Аныктама. Рационалдык сандар жана иррационалдык сандар чыныгы сандар деп аталат. Чыныгы сандардын көптүгү R тамгасы менен белгиленет жана төмөнкүдөй туюнтулат: R = Q 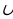 I.
I.
Чыныгы сандардын үстүндө кошуу, кемитүү, көбөйтүү, бөлүү, даража-га көтөрүү жана тамыр чыгаруу амалдары аткарылат.
Чыныгы сандардын үстүнөн аткарылуучу кошуу жана көбөйтүү амалдары орун алмаштыруу, топтоштуруу жана бөлүштүрүү касиеттерине ээ.
Чыныгы сандардын үстүнөн аткарылуучу даражага көтөрүү амалы төмөнкү касиеттерге ээ.
Ар кандай r жана s рационалдык сандары жана каалагандай 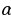 жана
жана 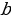 оң сандар үчүн төмөнкү барабардыктар орун алат:
оң сандар үчүн төмөнкү барабардыктар орун алат:
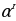
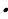
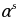 =
= 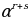 .
.
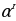 :
: 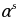 =
= 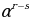 .
.
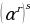 =
= 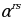 .
.
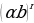 =
= 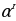
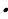
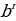 .
.
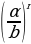 =
= 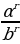 .
.
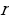 – рационалдык саны жана 0
– рационалдык саны жана 0 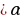
 b сандары берилген болсун. Анда r
b сандары берилген болсун. Анда r 0 болгондо
0 болгондо 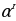

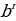 , ал эми r
, ал эми r 0 болгондо
0 болгондо 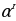

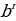 .
.
Ар кандай r жана s рационалдык сандары үчүн r  s барабар-сыздыгынан төмөнкү келип чыгат:
s барабар-сыздыгынан төмөнкү келип чыгат:
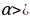 1 болгондо
1 болгондо 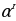

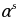 , ал эми 0
, ал эми 0
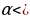 1 болгондо
1 болгондо 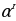

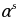 болот.
болот.
Өз алдынча иштөө үчүн тапшырмалар:
Эсептегиле
№1
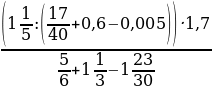 +
+ 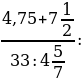 0,25; b)
0,25; b)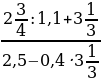 :
: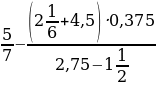
№2
24,57:3,5+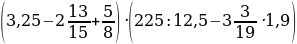
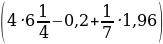 ·
·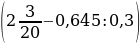
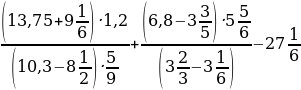 ; b)
; b) 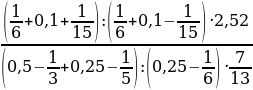
№4
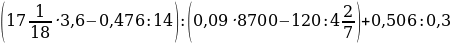
1,35:2,7+6,02-5,9+
№5
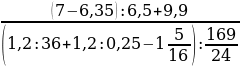 ; b)
; b) 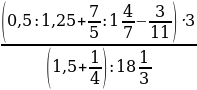
№6
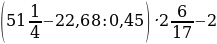 ; b)
; b) 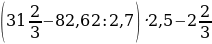
№7
26: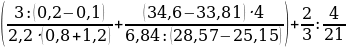
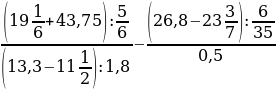
№8
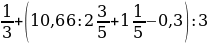 ; b)
; b) 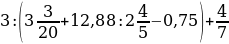
№9
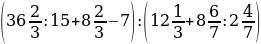 ; b)
; b) 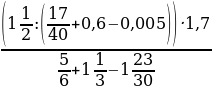
№10
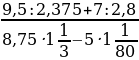 ; b)
; b) 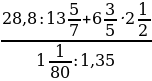 ·
·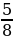
№11
0,8+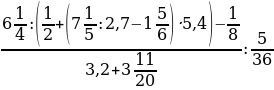
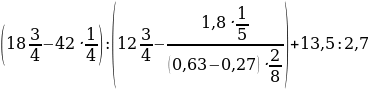







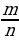 көрүнүшүндөгү сандар рационалдык сандар деп аталат, мында m саны бүтүн сан, ал эми n саны натуралдык сан. Мисалы,
көрүнүшүндөгү сандар рационалдык сандар деп аталат, мында m саны бүтүн сан, ал эми n саны натуралдык сан. Мисалы, 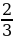 ,
, 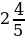 ,
, 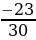 ж. б. сандар. Рационалдык сандардын көптүгү Q тамгасы менен белгиленет жана жалпы түрдө төмөнкүдөй белгиленет: Q
ж. б. сандар. Рационалдык сандардын көптүгү Q тамгасы менен белгиленет жана жалпы түрдө төмөнкүдөй белгиленет: Q  {
{ Q |
Q | 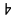 m
m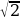 ,
, 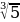 , e, π, sin
, e, π, sin 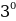 , log23 ж. б. Иррационалдык сандардын көптүгү I тамгасы менен белгиленет.
, log23 ж. б. Иррационалдык сандардын көптүгү I тамгасы менен белгиленет.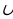 I.
I.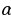 жана
жана 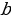 оң сандар үчүн төмөнкү барабардыктар орун алат:
оң сандар үчүн төмөнкү барабардыктар орун алат: 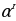
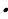
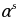 =
= 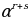 .
.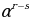 .
.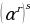 =
= 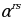 .
.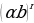 =
= 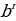 .
.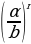 =
= 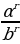 .
.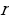 – рационалдык саны жана 0
– рационалдык саны жана 0 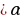
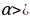 1 болгондо
1 болгондо 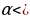 1 болгондо
1 болгондо 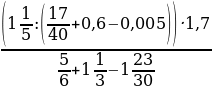 +
+ 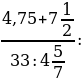 0,25; b)
0,25; b)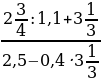 :
: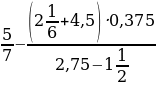
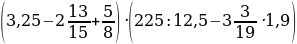
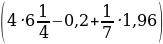 ·
·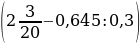
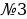
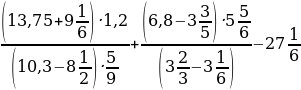 ; b)
; b) 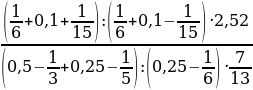
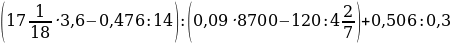

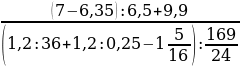 ; b)
; b) 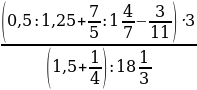
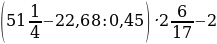 ; b)
; b) 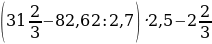
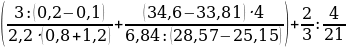
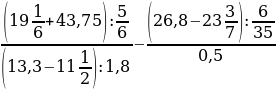
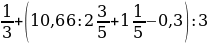 ; b)
; b) 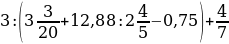
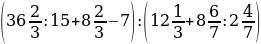 ; b)
; b) 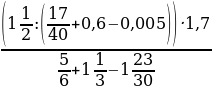
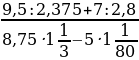 ; b)
; b) 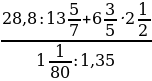 ·
·