Просмотр содержимого презентации
«algebr_drobi»

Алгебраические дроби

Алгебраическая дробь
- Область допустимых значений

дробь
Алгебраическая
Дробь
В алгебраической дроби
числитель и знаменатель
многочлены
Многочлен
одночленов
сумма
произведение чисел и степеней
переменных с натуральными
показателями.
Одночлен

P – числитель алгебраической дроби;
Q – знаменатель алгебраической дроби.

Являются ли данные выражения алгебраической дробью?
!!! Многочлен это частный
случай алгебраической дроби.

Найдите значение алгебраической дроби.
Делить на нуль нельзя
Значения, при которых знаменатель дроби
обращается в нуль называются
недопустимыми значениями переменной

Найдите допустимые значения алгебраической дроби

Алгоритм нахождения допустимых значений дроби:
- Найти значение переменной, при которых знаменатель дроби обращается в нуль.
2. Исключить эти значения из множества чисел.
Пример:
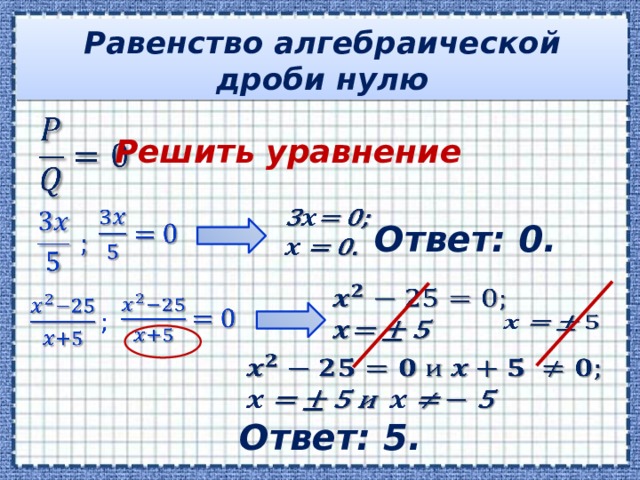
Равенство алгебраической дроби нулю
Решить уравнение
Ответ: 0.
Ответ: 5.

При каких значениях переменной алгебраическая дробь равна нулю?
Нет решений.

Алгоритм нахождения значений переменной, при которых дробь равна нулю:
- Найти значение переменной, при которых числитель дроби обращается в нуль.
2. Исключить значения переменных, при которых знаменатель дроби обращается в нуль.

Самостоятельная работа
1 вариант
2 вариант
1. Найдите значение алгебраической дроби
- 1
- 3
2. Найдите допустимые значения переменной
х любое, кроме х = -7
х любое, кроме х = 8
у любое, кроме у = -1 и у = 4
у любое, кроме у = 5 и у = -3
3. При каком значении переменной дробь равна нулю?
х = 8
х = - 9
у = 2
у = 4

Печатные источники
«Алгебра 8 класс», часть 1, учебник,
под редакцией А.Г. Мордковича,
Мнемозина, 2007 г.
Шаблон оформления презентации
Автор:
Ермолаева Ирина Алексеевна
Название сайта:
http://www.uchportal.ru/load/305-1-0-18319





























