СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока

Был в сети 04.05.2025 18:43
Коваль Евгений Алексеевич
Учитель информатики
51 год
Местоположение
РОССИЯ, ПОЛЯРНЫЕ ЗОРИ
Специализация
Алгоритм по решению задач на поиск количества различных путей в графе
Категория:
Информатика
21.02.2024 22:05


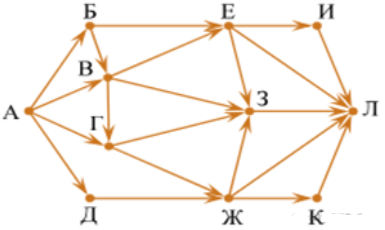
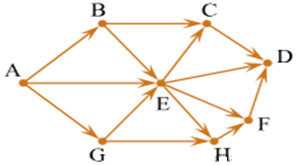 Задача. На рисунке - схема дорог, связывающих города А, B, C, D, E, G, H, F. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города A в город D?
Задача. На рисунке - схема дорог, связывающих города А, B, C, D, E, G, H, F. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города A в город D?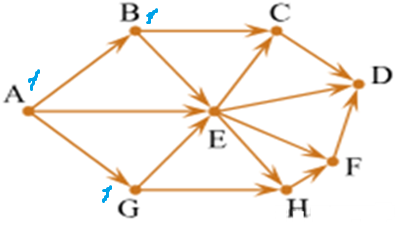
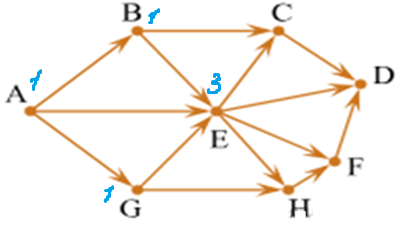
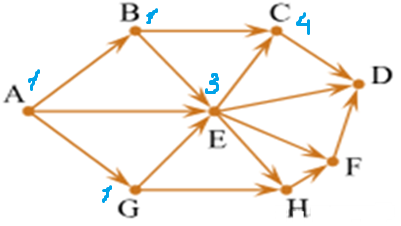
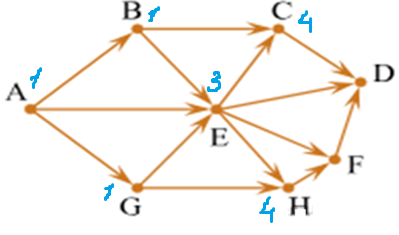
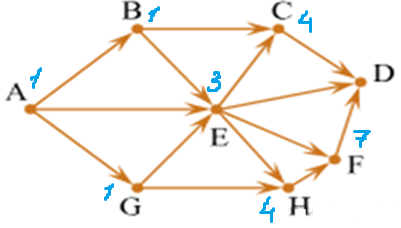
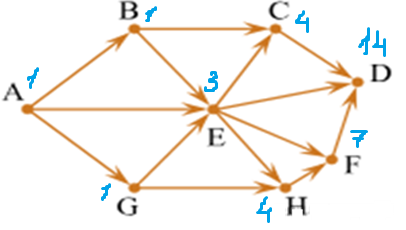
 б)
б)