Архимедовы тела

АРХИМЕДОВЫ ТЕЛА

.

АРХИМЕД

Архимед (ок. 287-212 г. до н. э.) - древнегреческий механик и математик, родом из Сиракуз (Сицилия).

Разработал предвосхитившие интегральное исчисление методы нахождения площадей поверхностей и объемов различных фигур и тел. В трудах по статике и гидростатике (закон Архимеда) дал образцы применения математики в естествознании и технике.  

Автор многих изобретений (архимедов винт, определение составов сплавов взвешиванием в воде, системы для поднятия больших тяжестей, военные метательные машины и другое). Организатор инженерной обороны Сиракуз против римлян; был убит при взятии римскими войсками города.

Вклад Архимеда в теорию многогранников - описание 13 полуправильных выпуклых однородных многогранников (архимедовых тел). До нашего времени эта работа Архимеда не сохранилась, но ссылки на нее имеются у Паппа.

Папп Александрийский (2-я половина III в. н. э.) - математик, жил и работал в Александрии. В труде "Математическое собрание" (книги I-VIII) изложил наиболее существенные результаты более ранних авторов, с улучшением и видоизменением известных теорем и доказательств. Многое не дошедшие до нас работы древних математиков известны только благодаря ссылкам на них Паппа. В частности, он ссылается на утерянную работу Архимеда  о полуправильных выпуклых однородных многогранниках.

Архимедовыми телами называются полуправильные однородные выпуклые многогранники , то есть выпуклые многогранники, все многогранные углы которых равны, а грани - правильные многоугольники нескольких типов (этим они отличаются от платоновых тел, грани которых - правильные многоугольники одного типа).

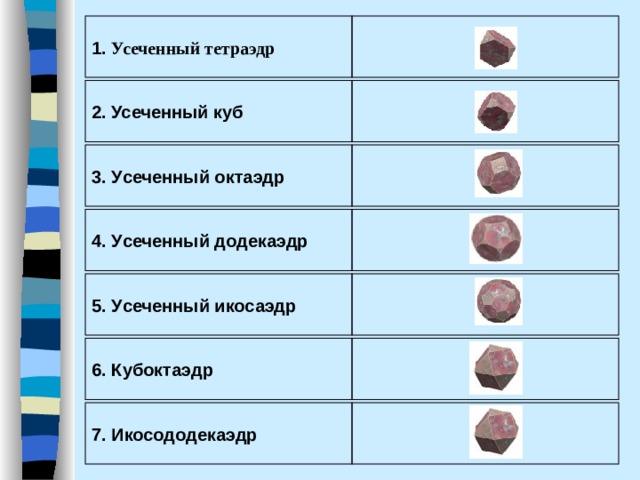
1. Усеченный тетраэдр

2. Усеченный куб

3. У сеченный октаэдр        

4. У сеченный додекаэдр 

5. У сеченный икосаэдр  

6. К убоктаэдр  

7. И косододекаэдр 

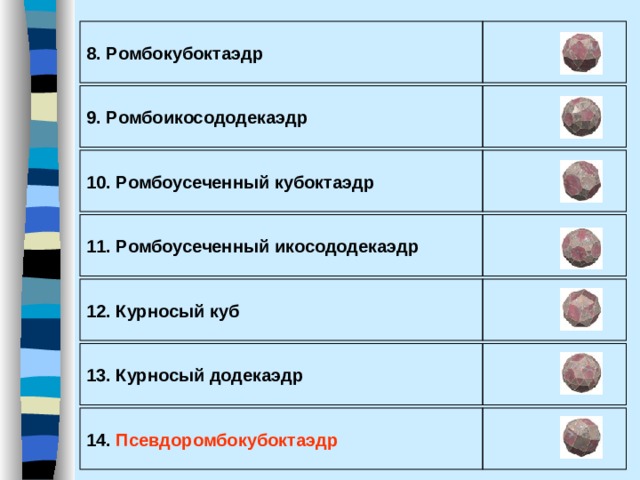
8. Р омбокубоктаэдр 

9. Р омбоикосододекаэдр 

10. Р омбоусеченный кубоктаэдр 

11. Р омбоусеченный икосододекаэдр 

12. К урносый куб  

13. К урносый додекаэдр 

14. П севдоромбокубоктаэдр 

Выводы:

- Открытие тринадцати полуправильных выпуклых многогранников приписывается Архимеду, впервые перечислившего их в не дошедшей до нас работе. Ссылки на эту работу имеются в трудах математика Паппа. - Т еорией этих тел занимался также Кеплер . - Относительно недавно (в конце 50-х - начале 60-х годов XX века) несколько математиков практически одновременно, независимо друг от друга указали на существование еще одного, ранее неизвестного полуправильного выпуклого многогранника - псевдоромбокубоктаэдра . Однако не все специалисты согласны с причислением этого многогранника к архимедовым телам.

ТВОРЧЕСКИЕ РАБОТЫ УЧАЩИХСЯ МОУ СОШ №1

Звездчатые формы

и соединения

Выпуклые однородные

многогранники

Усеченный

тетраэдр

Октаэдр

Кеплера

Завершающая

звездчатая

форма

икосододекаэдра

Малый

звездчатый

додекаэдр

Кубооктаэдр

6-я звезчатая

форма

икосаэдра

Ромбоусеченный

кубооктаэдр

9-я звезчатая

форма

икосаэдра

Ромбокубо-

октаэдр

Соединение

пяти

октаэдров

Курносый куб

ТВОРЧЕСКИЕ РАБОТЫ УЧАЩИХСЯ МОУ СОШ №1

Невыпуклые однородные многогранники

10-я звезчатая

форма

икосододекаэдра

Большой

додекогемидодекаэдр

Октагемиоктаэдр

Додекододекаэдр

3-я звезчатая

форма

кубооктаэдра

Усеченный большой

додекаэдр

Большой

икосододэкаэдр

Звездчатый октаэдр

ТВОРЧЕСКИЕ РАБОТЫ УЧАЩИХСЯ МОУ СОШ №1

Под руководством учителя математики – Родич В.Г.

Список источников :

• Афонькин С.Ю. Октаэдр и другие фигуры // Афонькин С.Ю. волшебные шары: Оригами.- М., 2001.- с. 178-180.

• Математический энциклопедический словарь «Советская энциклопедия», 1988г.
• Г.М. Клейнер «Математика и научная картина мира».
• М. Веннинджер «Модели многогранников»М. «Мир»,1974г