Арксинус и арккосинус числа

Урок алгебры в 10 классе

Работам устно

• Определите знак произведения

Sin157 °·sin275°·cos157°

Cos73°·cos140°·cos(-384°)

• Существует ли угол, для которого

• Упростите выражение:

Sin² α +cos² α =

1-cos² α =

Sin ² α – 1=

Вычислите

Определение арксинуса, арккосинуса числа а

Цель урока: ввести понятие арксинуса и арккосинуса числа; рассмотреть их свойства и научиться применять при упрощении выражений

Арксинус числа а , |а | ≤ 1 есть такое число α из промежутка [– π / 2; π / 2 ], синус которого равен числу а

Sin

π /2

arc sin ( – a ) = – arc sin a

1

arc sin a

а

α

– α

x

– a

-1

arc sin ( – a )

- π /2

Sin

π /2

Вычислите :

- π /2

Ищу число из отрезка

[ - π /2; π /2] , синус которого равен …

Арккосинус числа а , |а | ≤ 1 есть такое число α из промежутка [ 0; π ], косинус которого равен а

Sin

arc cos a

arc со s ( – a )

α

0

π

Cos

-1

1

– a

а

arc cos ( – a ) = π – arc cos a

Вычислите :

Cos

π

0

Ищу число из отрезка [0; π ] , косинус которого равен…..

Имеет ли смысл выражение?

а rcsin (-1/2) arccos arcsin

да нет нет

а rcsin 1,5 arccos arccos

нет да да

Историческая справка.

• Современные обозначения arcsin и arccos появляются в 1772 в работах великого математика Шерфера и известного французского ученого Ж.Л. Лагранжа, хотя несколько ранее их уже рассматривал Д. Бернули, который употреблял иную символику. Но общепринятыми эти символы стали лишь в конце XVIII столетия. Приставка « arc » происходит от латинского « arcus » (лук, дуга), что вполне согласуется со смыслом понятия: arcsin x , например, - это угол (а можно сказать и дуга), синус которого равен x .

π

1

=

arcsin

6

2

3

π

3

arcsin

=

2

π

1

-

)

(

arcsin

-

6

=

2

π

arcsin

1 =

2

π

2

arcsin

-

=

(

)

4

2

10

π

1

3

arccos

=

2

π

3

arccos

=

2

6

2 π

1

1

arccos

)

arccos

π ̶

=

−

=

(

2

2

3

2

3 π

)

(

arccos

=

2

4

π

0

=

arccos

2

Работаем вместе

• № 7.78
• № 7.86
• № 7.100(а,б,в)
• № 101 ( а,б,в)
• № 102
• № 103

Домашнее задание

• П. 7.5, 7.6, 7.8

№ 7.79

№ 7.87

№ 7.100(г,д,е)

№ 101 ( г,д,е)

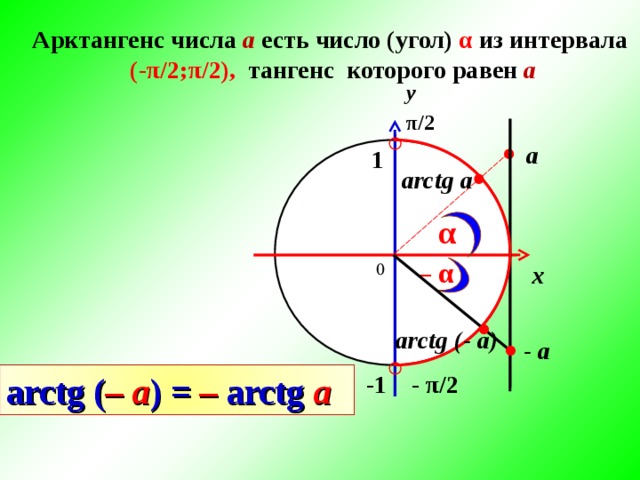
Арктангенс числа а есть число (угол) α из интервала

(- π /2; π /2), тангенс которого равен а

у

π /2

○

а

1

arctg a

α

– α

х

0

arctg (- a )

- а

○

- π /2

arctg ( – a ) = – arctg a

-1

Арккотангенс числа а есть число (угол)

α из интервала (0; π ),

котангенс которого равен а

а

- а

1

у

arcctg (- a)

arcctg a

α

π

х

○

○

0

0

-1

arcctg ( – a ) = π – arcctg a

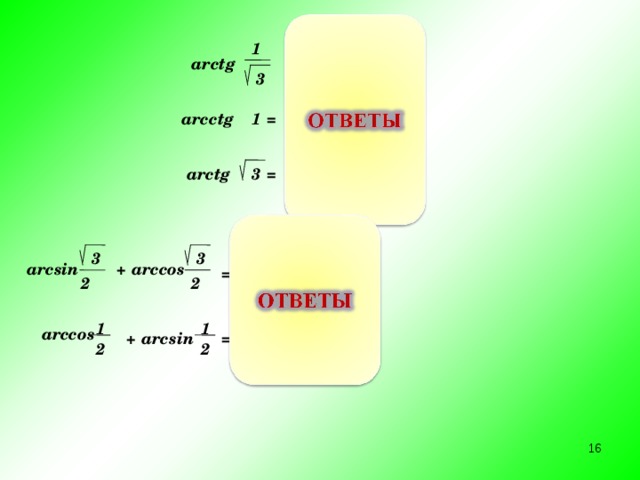
1

П

ar с tg

=

6

3

П

ar с ctg

1

=

4

П

3

ar с tg

=

3

3

3

П

П

П

+

arccos

arcsin

=

+

=

6

3

2

2

2

1

П

1

П

arccos

П

+

=

+

=

arcsin

2

2

6

2

3

16