План теоретического урока № _
| Группы
|
|
|
|
|
|
|
|
|
|
| Дата проведения урока |
|
|
|
|
|
|
|
|
|
Название учебного предмета: алгебра
Тема: Бесконечно убывающая геометрическая прогрессия
Цель урока:
а) Образовательная: формирование представлений о бесконечно убывающей геометрической прогрессии, о сумме бесконечно убывающей геометрической прогрессии, умений решать задачи на нахождение суммы бесконечно убывающей геометрической прогрессии. переменной.__________________________________________________
б) Воспитательная: - воспитание потребности к самообразованию, привитие интереса к предмету.- -интегрироваться в группу сверстников и строить продуктивное взаимодействие;
- воспитывать ответственность и аккуратность.
в) Развивающая1. развитие познавательной активности учащихся, связной речи; критического мышления; умения работать и взаимодействовать в группе одноклассников.
Ожидаемые результаты: - после освоения темы учащиеся будут иметь следующие знания и умения:
-Зная формулы геометрической прогрессии, уметь решать интересные задачи литературного, исторического и практического содержания на прогрессию.
-уметь отстаивать свою точку зрения и работать в парах, в коллективе.
-анализировать условия и требования задачи; выбирать обобщенные стратегии решения задачи.
Методы обучения: Лекция, диспут, составление кластера, конспект лекции, частично – поисковый .
Критерии оценки: поэтапность, объективность, получение знания, самостоятельно излагать свое мнение
Технические средства и источники информации: доска, мел, карточки, презентация,учебник алгебры 9 класса
Вид урока Комбинированный
Отведенное время на урок: 45 минут
Домашнее задание: § 33 стр.176 №№416-418
Преподаватель Розыбакиева Л.Д. _________________
Председатель МО Сатдарова Н.М. _________________
Технологическая карта теоретического урока в 9-х классах по теме:
«Бесконечно убывающая геометрическая прогрессия»
| Этапы урока | Методы обучения | Деятельность учителя | Деятельность учащихся | Средства обучения |
| I.Организационный момент |
| Учитель приветствует детей. |
| Кундалик. Учебник алгебры 9 класс, доска мел,мультимедиа |
| II.Актуализация знаний. | Слайд 1, 2
Компьютерное тестирование | - Мы продолжаем изучение геометрической прогрессии. Вспомним, какая последовательность называется геометрической прогрессией? Выполните тест. Отметки по желанию учащихся выставляются в журнал. | Ученики на компьютерах выполняют тест.
Анализ ответов. Ответы к тесту выводятся на экран. | Кундалик. Учебник алгебры 9 класс, доска мел,мультимедиа |
| III.Стадия вызова
Прием «Корзина идей»
Постановка цели урока | Слайд 3
Макет корзины. Слайд 4
Слайд 5
вопросно-ответная форма, диспут
Слайд 6
| - Зная формулы геометрической прогрессии, мы умеем решать интересные задачи литературного, исторического и практического содержания на прогрессию. Решите еще одну задачу про героя троянской войны Ахиллеса: «Ахиллес бежит со скоростью в 10 раз быстрее, чем черепаха и изначально находится на расстоянии 1000 шагов от нее. Какое общее расстояние, пройденное Ахиллесом до встречи с черепахой?» - Обсудите в парах и составьте план решения задачи. Все идеи «сбрасываем в корзину» Все мнения, выражения записываются учителем или учениками в «корзине» идей на доске (без комментариев), даже если они ошибочны. Основное условие – не повторять то, что уже было сказано другими.
- Попробуем систематизировать полученную информацию.
- Таким образом, получаем последовательность 1000, 100, 10, 1, 0,1, 0,01…
- Что можете сказать о данной последовательности?
- Конечной или бесконечной? Убывающей или возрастающей? Какой знаменатель прогрессии?
- Как вычислить общее расстояние, пройденное Ахиллесом до встречи с черепахой?
- Вычислите сумму по известным формулам геометрической прогрессии.
- На какие вопросы хотели бы получить ответы?
- Как назовем тему сегодняшнего урока?
- Открываем тетради, пишем тему урока. Учитель конкретизирует цели урока, обращает внимание на «идеи в корзине» и вместе с учащимися обсуждают, какие идеи ошибочны, какие ближе к ответу, какие необходимо еще уточнить. Исправляются ошибки. |
Учащиеся обсуждают решение в парах.
Выражения записываются учениками на доске.
- Когда Ахиллес пробежит 1000 шагов, черепаха проползет в 10 раз меньше, то есть 100 шагов. Расстояние между Ахиллесом и черепахой будет 100 шагов. Тогда Ахиллес пробежит 100 шагов, а черепаха проползет 10 шагов. После этого между Ахиллесом и черепахой будет расстояние в 10 шагов. Когда Ахиллес пройдет 10 шагов, черепаха проползет 1 шаг. Когда Ахиллес пройдет 1 шаг, черепаха проползет еще 0, 1 шага и все равно будет дальше него. Так можно продолжать до бесконечности. - Последовательность является геометрической прогрессией.
- Бесконечно убывающая. Знаменатель 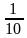 . .
- Сложить числа 1000+100+10+1+ 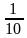 + + 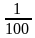 + + 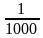 +… +…
- Невозможно. Членов прогрессии бесконечно.
- Как определить, является геометрическая прогрессия убывающей? - Как вычислить сумму, если геометрическая прогрессия убывающая и бесконечная? - Сумма бесконечно убывающей прогрессии.
Дети записывают тему. | Доска, мел, раздаточный материал, схемы, таблицы |
| IV.Стадия осмысления
Первичное закрепление | Каждая группа работает с учебником и дополнительным материалом на компьютере.
Слайд 7
Слайд 8
Слайд 9 | - Найдем сумму разными способами. Первая группа вычисляет сумму первым способом, вторая – вторым, третья – третьим способом. IV группа выводит формулу суммы, используя материал учебника. Для этого в группе разбираете указанный выше способ нахождения суммы и применяете для нашей последовательности. - Командиры с помощью членов группы представляют свое решение. - Какое общее расстояние, пройденное Ахиллесом до встречи с черепахой?
- Какой вывод можно сделать из этих решений?
- Какое условие должно выполняться, чтобы геометрическая прогрессия была бесконечно убывающей? - Что для этого необходимо знать?
- Решите задачу: «Один из учеников, вызванный к доске, должен идти от стола к двери по прямой. Первый шаг он делает длиной 1метр, второй -1/2 м., третий 1/4 м и т. д. так, что длина следующего шага в 2 раза меньше длины предыдущего. Дойдет ли ученик до двери, если расстояние от стола до двери по прямой 3 метра?» - Вернемся к задаче про Ахиллеса и черепаху. Расстояние, которое потребуется преодолеть Ахиллесу, чтобы догнать черепаху, равно
- Все согласны с таким ответом: быстрый Ахиллес догонит медлительную черепаху.
- Всем известно, что такое софизмы. Очень интересны математические софизмы древнегреческих философов-математиков. Разгадать один из самых известных софизмов древнегреческого философа Зенона — парадокс Ахиллеса и черепахи, будет вашим домашним заданием. | Класс делится на 4 группы. Находят сумму различными способами. Каждая группа свое решение оформляет в тетради. Для презентации работы используют документ-камеру, доску. Последней выступает группа, вычисляющая сумму по формуле суммы геометрической прогрессии.
- S=1000+100+10+1+0,1+…= 1111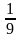 . . Расстояние, которое потребуется преодолеть Ахиллесу, чтобы догнать черепаху, равно 1111 и одна девятая шага (0,111…=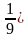 . .
- Мы нашли сумму бесконечной прогрессии. - Даже бесконечное количество слагаемых в сумме может давать конечную величину, если пренебречь малой величиной
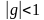
- Первый член прогрессии и знаменатель. S=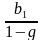
Дети формулу записывают в тетрадях. Индивидуальная работа. Решение. 1, 1/2, 1/4, 1/8, … S=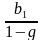
S=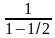 =2 =2 Ответ: нет.
- 1111 и одна девятая шага (0,111…= 1/9).
- Да. Ахиллес догонит черепаху и обгонит ее.
| Учебник алгебры 9 класс, доска мел,мультимедиа |
|
V.Стадия рефлексии.
Заключительный этап |
|
- Предлагаю каждому составить рассказ (не более 5 предложений) по теме: «Сумма бесконечно убывающей геометрической прогрессии». Работа по вариантам. Учитель просит озвучить несколько рассказов и обсудить: если мама с папой прочитают такой рассказ, все ли им будет понятно?
- Подведем итоги. - Что нового узнали на уроке? - Цели урока выполнены? - Что интересного было на уроке? - Что вызвало затруднение? Какие вопросы вы бы задали по этому поводу? - Не осталось ли в корзине идей? - Оценки. |
Учащиеся 1 варианта пишут от своего имени своим родителям; учащиеся 2 варианта пишут от своего имени одноклассникам. Пример рассказа: «Мама и папа! Сегодня на уроке по теме "Сумма бесконечно убывающей геометрической прогрессии " я узнал, что сумма бесконечно убывающей геометрической прогрессии конечное число. Узнал, что в математике бесконечно малой величиной можно пренебречь. Чтобы вычислить сумму бесконечно убывающей геометрической прогрессии я должен знать формулу, первый член прогрессии и знаменатель. Меня заинтересовали софизмы». |
Учебник алгебры 9 класс, доска мел,мультимедиа |
| VI. Домашнее задание | Слайд 10 | - Разгадать парадокс Ахиллеса и черепахи. - Почему данная задача древним представлялась неразрешимою? - Какую роль играют математические софизмы?
|
|
|
Домашнее задание: § 33 стр.176 №№416-418
Тест
Выберите верный ответ
1. Геометрическая прогрессия - это
а) числовая последовательность, каждый член которой, начиная со второго, равен сумме предыдущего члена и одного и того же числа d;
б) числовая последовательность, каждый член которой, начиная со второго, получается из предыдущего члена умножением его на одно и то же число g;
в) числовая последовательность, все члены которой отличны от нуля и каждый член которой, начиная со второго, получается из предыдущего члена умножением его на одно и то же число g.
2. Какая из последовательностей является геометрической прогрессией
а) 13, 25, 37, 49,…
б) -10, 20, -40, 80,…
в) -7, -2, 3, 0,…?
3. Какая геометрическая прогрессия является убывающей
а) -6, -3, -1,5,…
б) 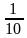 ,
, 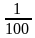 ,
, 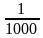 ,
, 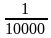 ,…
,…
в) -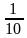 , -
, - 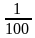 , -
, - 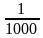 , -
, - 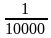 ,…?
,…?
4. В геометрической прогрессии 0,1, 0,001, 0,00001,…
найдите знаменатель
а) 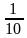
б) 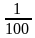
в) 0, 0001
5. Формула для нахождения суммы n-первых членов геометрической прогрессии
а) Sn=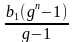
б) Sn=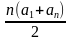
в) Sn=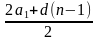 ·n.
·n.
Нахождение суммы бесконечно убывающей геометрической прогрессии
Способ 1.
Обозначим сумму через S:
S= 1000+100+10+1+ 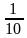 +
+ 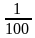 +
+ 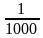 +…
+…
Тогда 10S=10000+1000+100+10+1+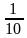 …
…
10S=10000+S,
9S=10000,
S=10000/9,
S=1111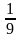 .
.
Способ 2.
Ахиллес догонит черепаху, пробежав некоторое расстояние S. За это время черепаха, скорость которого в 10 раз меньше, проползет расстояние  , и расстояние между ними уменьшится на S-
, и расстояние между ними уменьшится на S- . =
. = . Если в начале оно равнялось 1000 шагам, а в момент встречи стало нулевым, то
. Если в начале оно равнялось 1000 шагам, а в момент встречи стало нулевым, то  =1000 иS=10000/9.
=1000 иS=10000/9.
Способ 3.
По формуле суммы геометрической прогрессии Sn=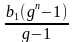 , где g=
, где g=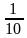 , а с ростом n
, а с ростом n  бесконечно мало, и им можно пренебречь. Тогда Sn=
бесконечно мало, и им можно пренебречь. Тогда Sn= , Sn=
, Sn=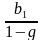 .
.
S= =
=






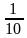 .
.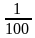 +
+ 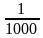 +…
+…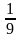 .
.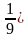 .
.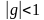
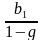
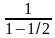 =2
=2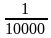 ,…
,…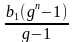
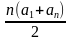
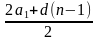 ·n.
·n.




















