Полное наименование образовательного учреждения
МБОУ им.Л.Н.Толстого филиал в с.Домачи
Лев-Толстовского муниципального района Липецкой области
Название секции
Математика
Название работы
Быстрый счёт без калькулятора
Фамилия, имя, отчество обучающегося
Нистратова Дарья Николаевна
Класс
Ученица 6 класса
Фамилия, имя, отчество руководителя
Кузовлева Марина Борисовна
Должность
Учитель математики
2017 год
Оглавление
I.Введение……………………………………………………………………………………3
II. Основная часть……………………………………………………………………………………...4
Глава 1.История возникновения счёта……………………………………………………………….4
1.1.Как люди научились считать……………………………………………………………….....….4
1.2. Счётные устройства…………………………………………………………………………..…..4
1.3. Люди-счётчики……………………………………………………………………………….…...4
Глава 2. Старинные способы умножения……………………………………………………………5
2.1. Русский крестьянский способ умножения…………………………………..……………….….5
2.2.Итальянский способ умножения ……………………………………………..…………………..5
2.3. Индийский способ умножения……………………………………………………………..….....5
2.4. Японский способ умножения ……………………...……………………………………..……...6
2.5.Умножение на пальцах на 9……………………………………………………............................6
Глава 3. Секреты быстрого счёта…………………………………………………………………….6
Глава 4. Практическая часть……………………………………………………………………….....7
4.1. Анкетирование учащихся 3-4, 6- 9 классов………………………………..…………….……...7
4.2. Обучение учащихся 3 и 4 классов быстрому счёту……………………………….....…..……..7
4.3.Проведение мастер-класс для учащихся 6-9 классов……………………………………...…....7
4.4. Исследовательская работа по проведению контрольных измерений…………………..……..7
4.5. Мониторинг результатов контрольных измерений в 6-9 классах………………………..........8
III.Заключение…………………………………………………………………….…….......................9
IV.Список использованной литературы и интернет-ресурсов………………………………..…..10
V.Приложение………………………………………………………………………………………..11
Введение
Глава 1.История возникновения счёта
Человеку в повседневной жизни невозможно обойтись без вычислений. Поэтому на уроках математики, нас в первую очередь учат выполнять действия над числами. Умножаем, делим, складываем и вычитаем мы привычными для всех способами, которые изучаются в школе.Мне стало интересно, а есть ли еще какие-нибудь способы вычислений? Оказалось, что можно умножать не только так, как предлагают нам в учебниках математики, но и по-другому. Захотелось узнать эти и другие способы вычислений, а также сравнить их с сегодняшними. Используя интернет-ресурсы и дополнительную литературу, я узнала много необычных способов умножений.
Я выбрала проект на тему «Быстрый счёт без калькулятора» потому, что именно сейчас мне необходимо усовершенствовать навыки устного счёта, так как приближается основной государственный экзамен, где у меня точно не будет возможности воспользоваться калькулятором. Поэтому в своей работе я хочу показать, как можно считать быстро и правильно и что процесс выполнения действий может быть не только полезным, но и интересным занятием.
Актуальность этой темы заключается в следующем: быстрый счет помогает людям в повседневной жизни, а нам ученикам на «хорошо» и «отлично» заниматься по математике.
Цель проекта: найти и освоить нестандартные приёмы счёта, позволяющие выполнить действия с числами быстро и безошибочно.
Задачи:
Используядополнительную литературу и Интернет- ресурсы, изучить методы и приемы быстрого счета.
Рассмотреть несколько старинных методов, которые можно использовать и в наши дни.
Обучить учащихся 3 и 4 классов быстрому счёту.
Провести мастер-класс в 6,7,8,9 классах по данной теме, проанализировать и сравнить результативность счета до и после ознакомления с некоторыми приемами быстрого счёта.
Составить буклет «Приемы быстрого счета» в помощь ученику.
Гипотеза:Существуют ли специальные способы выполнения действий, которые позволяют свести вычисления к устным, рассчитанные на ум «обычного» человека и не требующие уникальных способностей.
Основополагающий вопрос:как за короткое время научиться быстро, считать, если ты обыкновенный школьник, а не вундеркинд?
Глава 1. История возникновения счета
Как люди научились считать.
Никто не знает, как впервые появилось число, как первобытный человек начал считать. Однако десятки тысяч лет назад первобытный человек собирал плоды деревьев, ходил на охоту, ловил рыбу, научился делать каменный топор и нож, и ему приходилось считать различные предметы, с которыми он встречался в повседневной жизни. Таким образом, сам не замечая, человек начал считать и вычислять.
Для счёта люди использовали пальцы рук и ног. Ведь и маленькие дети тожеучатся считать по пальцам. Однако этот способ годился только в пределах20. Выход нашелся: считать на пальцах до 10, а затем начинать сначала, отдельно подсчитывая количество десятков. Система счисления на основе десяти возникла как естественное развитие пальцевого счета.
По мере развития речи люди начали использовать слова для обозначения чисел. Отпала необходимость показывать кому-то пальцы, камешки или реальные предметы, чтобы назвать их количество. Для изображения чисел стали применяться рисунки, чертежи или символы. Древние торговцы для удобства счета начали накладывать зерна и ракушки на специальную дощечку, которая со временем стала называться абаком.
1.2.Счётные устройства.За абаками были созданы арифмометры. Арифмометры- это настольная механическая вычислительная машина для выполнения четырёх математических действий. Русский арифмометр был сконструирован инженером Одиером в 1874 году.Долгое время популярным счётным устройством была логарифмическая линейка, изобретённая лондонским профессором Гунтером в 1625 году. Служила она до 20 века и была вытеснена микрокалькуляторами.Первую программно-управляемую вычислительную машину создал английский учёный Ч.Беббидж в 18 веке. Первую электронно-вычислительную машину «ЭНИАК» разработали в США в 1945 году.Первая отечественная ЭВМ была разработана в 1947 году под руководством академика С.А. Лебедева. Современный помощник вычислений – микрокалькулятор - прибор, позволяющий производить сложные вычисления за короткий промежуток времени. Но, несмотря уже на имеющиеся удобства, процесс развития вычислительной техники продолжается.
1.3Люди – счетчики. Как ранее, так и сейчас существовали и существуют люди, обладающие феноменальными способностями к счету. Расскажу о некоторых из них. ДаниэлМакКартнижил в 19 веке в США, который с рождения был слепым. Он не только моментально умножал и складывал громадные числа, он также обладал идеальной памятью, и мог рассказать о любом дне своей жизни, начиная с 9 лет. За десять минут он смог возвести число 89 в шестую степень. За три минуты он мог найти кубический корень с точностью до миллионных. Виллем Клейн жил в 20 веке в Нидерландах. Он занесен в книгу рекордов Гиннеса как человек, который смог извлечь корень 73 степени из пятисот -значного числа. У него ушло на это две минуты и 43 секунды.
Альберто Кото Гарсия жил в Испании -самый известный и титулованный арифметик-счетчик. Его мозг способен выполнять до 5-6 операций за секунду. Например, индийская женщина Шакунтала Дэви без особых проблем,буквально за несколько секунд извлекала квадратные и кубические корни из многозначных чисел. Одним из самых её удивительных достижений - перемножение двух 13-значных чисел за 28 секунд.
Жили подобные люди-счетчики и в России.Владимир Степанович Зубрицкий- юный гений, который с 7 лет выступал в цирке с номером «Живая счетная машина», он производил сложные арифметические вычисления в уме. Владимир был сыном цирковых артистов. Игорь Алексеевич Шелушков - советский человек-счётчик. Он запоминал числа на вращающихся досках и извлекал из них корни. В Институте кибернетики в Киеве, было устроено состязание Игоря Алексеевича с ЭВМ третьего поколения. Он извлек корень из огромного числа быстрее, а именно за 18 сек, чем быстродействующий компьютер за 10 минут, ему было тогда 22 года.
Такие люди всегда очень интересовали психологов, врачей и математиков, которые старались выяснить, в чем секрет их способностей.Мне стало интересно, неужели нельзя обычному человеку обучиться быстро считать в уме? Как этого достигнуть? Для этого я изучила старинные способы быстрого счета:
Глава 2. Старинные способы умножения
2.1. Русский крестьянский способ умножения. В России 2-3 века назад среди крестьян некоторых губерний был распространён способ, который не требовал знание всей таблицы умножения. Надо было лишь умножать и делить на 2. Этот способ получил название крестьянского.Вот пример: Нам нужно 47 умножить на 35. Вот как бы решили этот пример 3-4 века назад наши предки: -запишем числа на одной строчке, проведём между ними вертикальную черту;левое число будем делить на 2, правое умножать на 2 (если при делении возникает остаток, то остаток отбрасываем); деление заканчивается, когда слева появится единица;вычёркиваем слева те строчки, в которых стоят слевачётные числа;далее оставшиеся справа числа складывает- это результат:35+70+140+280+1120и получаем в ответе 1645.Этот способ громоздкий, но он имеет право на существование.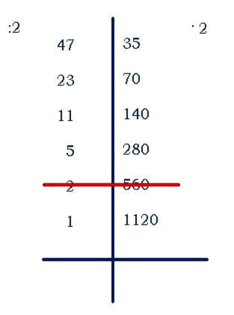
2.2 Итальянский способ умножения Аль-Хорезми («метод решётки»). В Италии, а также во многих странах Востока, этот способ приобрёл большую известность.Способ решётки ни в чём не уступает умножению столбиком. К тому же этот способ позволяет быстрее получить результат. Освоив его, вы сможете убедиться в этом сами. Например, умножим 621*357Для этого: 1. Вычерчиваем квадратную сетку и пишем одно из чисел над колонками, а второе по высоте.2. Умножаем число каждого ряда последовательно на числа каждой колонки.3. Если при умножении получается однозначное число, записываем вверху 0, а внизу это число. Заполняем всю сетку и складываем числа, следуя диагональным полосам. Начинаем складывать справа налево. Если сумма одной диагонали содержит десятки, то прибавляем их к единицам следующей диагонали. В результате получаем 22 169.
2.3 Индийский способ умножения(метод Ферроля). Этим способом пользовались жители Индии в 6 веке. Для получения единиц перемножают единицы множителей, для получения десятков, умножают десятки одного на единицы другого и наоборот и результаты складывают, для получения сотен перемножают десятки. Методом Ферроляпозволяетлегко перемножать устно двухзначные числа от 10 до 20.Например: 12х14=168 1 шаг 2х4=8, пишем 8 в разряд единиц;2 шаг 1х4+2х1=6, пишем 6 в разряд десятков;3 шаг1х1=1, пишем 1 в разряд сотен.Я познакомилась с этим способом на очень простом примере без перехода через разряд. Мои исследования показали, что им можно пользоваться и при умножении многозначных чисел.
2.4. Японский способ умножения (с помощью линий). Таблица умножения для нас — то, без чего не обойтись никак, краеугольный камень в изучении математики. А вот в Японии малыши 1 класса поначалу обходятся при расчетах без нее, лихо перемножая двух- и даже трехзначные числа. В этом им помогает метод линий, Допустим, нам надо умножить 12*13=156. Начертим следующий рисунок: этот рисунок состоит из 7 линий,числа изображаются в виде прямых линий, десятки и единицы отделяются промежутками и располагаются параллельно друг другу на плоскости. Каждый из множителей располагается под углом 45 градусов. Количество пересечения линий, образующих десятки при умножении двузначных чисел, будет первой цифрой в произведении. Точки пересечения десятков и единиц — вторая цифра результата, количество точек, образовавшихся при пересечении всех единиц - третья цифра.
2.5. Умножение на пальцах. Это просто. Чтобы умножить любое число от 1 до 9 на 9, посмотрите на руки. Загните палец, который соответствует умножаемому числу (например 9 x 4 – загните четвёртый палец), посчитайте пальцы до загнутого пальца - это десятки (в случае 9 x 4– это 3, затем посчитайте после загнутого пальца – это единицы (в нашем случае – 6). Ответ – 36.
Глава 3. Секреты быстрого счёта
3.1. Умножение двузначных и трёхзначных чисел на 11.При умножении двузначного числа на 11, нужно между цифрой единиц и цифрой десятков вписать сумму этих цифр, причем, если сумма цифр больше 10, то единицу нужно прибавить к старшему разряду (первой цифре).Например:45*11= 4(4+5)5=495 «Краешки сложи, в серединку положи» - эти слова помогут легко запомнить данный способ умножения на 11.Такой способ подходит не только для умножения двузначных чисел, но и трёхзначных чисел: 234*11= 2(2+3)(3+4)4= 2574
3.2. Возведение в квадрат двузначных и трёхзначных чисел, оканчивающихся цифрой 5Если вам нужно возвести в квадрат двузначное или трёхзначное число, заканчивающееся на 5, то вы можете сделать это очень просто в уме. нужно цифру десятков умножить на цифру, большую на единицу, и к полученному произведению приписать справа число 25.Например:65²=65*65= 4225
3.3.Умножение двузначного числа на 101.Для того, чтобы число умножить на 101, нужно приписать данное число к самому себе.Например:59*101=5959
3.4.Умножение чисел, у которых число десятков одинаково, а сумма единиц равна 10, например:42 ∙ 48=20161шаг4 ∙ (4+1)=20, пишем 20; 2шаг перемножаем единицы2*8=16, пишем 16.
3.5. Умножение двузначных чисел, оканчивающихся на "1, например51*31=1581
1шаг 5*3*100=1500; 2 шаг (5+3)*10=80; 3 шаг 1*1=1; 4 шагвсё сложить 1500+80+1=1581
3.6. Умножение чисел от 10 до 20, например, 16∙18=(16+8) ∙ 10+6 ∙ 8=288
шаг: к первому числу добавляют единицы от второго, и умножаем на 10;
шаг: единицы перемножают; 3шаг: складывают результат шага 1 с результатом шага 2.
3.7.Умножение на 22, 33, 44, 55,66,77,88,99. Чтобы умножить двузначное число на 22,33,44,55,66,77,88,99 нужно этот множитель представить в виде произведения однозначного числа на 11, выполнить умножение на однозначное число, а потом на 11.Например, 15*33=15*3*11=45*11=495
3.8.Особый способ умножения многозначных чисел. Этому способу не учат в школе.
999 973*999 990=999963000270
Получится в ответе число, состоящее из 12 цифр.
999 973*999 990 =
(1 000 000-27)*(1 000 000-10)
999 973-10=999 963 или 999 990-27=999 963 запишем это число в первые шесть клеток.
27*10=270 запишем их справа налево, недостающие цифры записать тремя нулями.
Глава 4. Практическая часть
4.1. Анкетирование учащихся 3-4, 6- 9 классов.
Для того чтобы выяснить, знают ли современные школьники другие способы выполнения арифметических действий, кроме умножения, сложения, вычитания столбиком и деления «уголком» и хотели бы узнать новые способы, я провела анкетирование в 3-4 и 6- 9 классах нашей школы. Задавала ребятам простые вопросы. Нужно ли уметь считать современному человеку?При изучении,каких школьных предметов требуется правильный счет? Знают ли они приемы быстрого счета? Хотели бы узнать другие способы быстрого счёта? В опросе приняли участие 21 человек.
Проанализировав результаты, я построила 4 круговых диаграммы и сделала вывод, что большинство учеников считает, что умение считать пригодится в жизни и необходимо в школе, особенно при изучении математики, физики, химии, а также при сдаче государственного экзамена в 9 классе. Приемы быстрого счета знают несколько учеников и почти все хотели бы научиться быстро,считать. Результаты анкетирования отражены в диаграммах. (Приложение №1).
4.2. Обучение учащихся 3 и 4 классов быстрому счёту. Для учащихся 3 и 4 класса я провела обучениев форме игры, используя красочную презентацию, я научила их двум старинным способам счёта: умножению на 9 с помощью пальцев рук и способу Аль-Хорезми, а также умножению двузначных чисел на 11,101,9,5, 25 и 8. Учащиеся начальных классов очень внимательно слушали объяснения, а затем на контрольных примерах успешно выполняли задания устно.
4.3.Проведение мастер-класс для учащихся 6-9 классов. Провела мастер- класс для учащихся 6-9 классов, обучила их пяти старинным способам вычислений и открыла им секреты быстрого счета. Учащиеся 6-9 классов освоили все старинные способы быстрого счета, особенно им понравился метод линий и метод решетки. А также обучила их секретам быстрого счёта, используя специальные правила.
4.4. Исследовательская работа по проведению контрольных измерений. Изучив методы быстрого счета, я отобрала для учащихся 6-9 классов самые распространенные и общедоступные задания. По согласованию с учителем математики, составила контрольные срезы, состоящие из 12 заданий, опираясь на данные методы. (Приложение 2).
Контрольные измерения в 6-9 классах я проводила в количестве 5 дней и подсчитала средний балл, выполненных заданий, а также время их выполнения.Главное условие – все вычисления ребята должны проводить в уме, используя любой приём вычисления. После проведения первого контрольного среза, мы разобрали допущенные ошибки, и я им показала еще несколько приемов быстрого счёта. Последующие четыре контрольных среза были проведены в последующие дни. При проведении их, я учитывала правильность решения и время выполнения. Все результаты сведены в таблицу, которую вы видите на слайде (Приложение №3, Приложение №4).
4.5.Мониторинг результатов контрольных измерений в 6-9 классах. Обработка результатов показала. На первом этапе письменно решено без ошибок– 68 % время- 10 минут. После изучения способов облегченных вычислений, во втором контрольном замере: решено – 73% время- 8 мин. После непродолжительной тренировки, в третьем контрольном замере : решено полностью устно– 88%, время-6мин , В четвёртом замере выполнено заданий – 90%, время 4,5 минуты, а в последнем замере выполнено заданий- 98 %, время 3 минуты. От замера к замеру количество допущенных ошибок уменьшилось, а правильно решенных заданий увеличилось. На примере учащихся 6-9 классов нашей школы, наглядно прослеживается динамика развития вычислительных навыков приемов устного счета. Я очень довольна тем, что вся работа, проделанная мною по отработке приёмов быстрого счёта, пригодится и мне и им в дальнейшей учёбе (Приложение №5).
Заключение.
Счет является простым и легким делом только тогда, когда владеешь особыми приемами и навыками. Наработка вычислительных навыков должна быть систематической, ежедневной, надо стремиться к тому, чтобы как можно больше освоить “хитрых” приемов. Таким образом, я убедилась, что моя гипотеза о том, что знание и использование приемов быстрого счета позволит свести вычисления к устным, рассчитанные на ум «обычного» человека и не требующие уникальных способностей подтвердилась.
Описывая старинные способы вычислений и современные приёмы быстрого счёта, я попыталась показать, что как в прошлом, так и в будущем, без математики, науки созданной разумом человека, не обойтись. В заключение подчеркну, что ученики 3,4,6-9 классов, принявшие участие в моём исследовании изменили своё отношение к быстрому счёту.Онипоняли, что устный счёт улучшает их вычислительные навыки, развивает механическую память, быстроту реакции, умение сосредоточиться. Вот так простые устные упражнения на каждом уроке математики могут развить каждого из нас. Нужно только стараться и усердно работать!
.
Список используемой литературы
Кордемский Б.А., Ахадов А.А. Удивительный мир чисел: Книга учащихся,- М. Просвещение, 1986г.
Минских Е.М. «От игры к знаниям», М., «Просвещение», 1982г
http://matsievsky.newmail.ru/sys-schi/file15.htm
htt://ru.wikipedia.org/wik
http://sch69.narod.ru/mod/1/6506/hystory.html
Энциклопедия для детей. “T.23”. Универсальный энциклопедический словарь \ ред. коллегия: М. Аксёнова, Е.Журавлёва, Д.Люри и др. – М.: Мир энциклопедий Аванта +, Астрель, 2008. – 688 с.
Ожегов С. И. Словарь русского языка :ок. 57000 слов/ Под ред. чл. – корр. АНСИР Н.Ю. Шведовой. – 20 – е изд.– М. : Просвещение, 2000. – 1012 с.
Приложение 1
Анкета для учащихся 3-4, 6-9 классов МБОУ им.Л.Н.Толстого филиала в с.Домачи
1.Зачем нужно современному человеку уметь считать?
а) пригодится в жизни;
б) чтобы хорошо учиться в школе;
в) чтобы быстро решать;
г) не обязательно уметь считать.
2. На каких уроках надо уметь считать?
а) математика; б) физика; в) химия; г) география; д) информатика.
3. Знаешь ли ты приемы быстрого счета?
а) да б) нет в) знаю частично; г) а зачем.
4. Хотел бы ты научиться быстро считать?
а) да; б) нет; в) не знаю.
Результаты анкетирования учащихся

Приложение 2
Задания для контрольных срезов учащимся 6-9 классов
МБОУ им.Л.Н.Толстого филиала в с.Домачи
Задания для контрольного среза №1
| 1. 45*11 | 2. 93*97 | 3. 86*84 | 4. 45² | 5. 280*1,5 | 6. 235*11
|
| 7. 56*101 | 8. 83*87 | 9. 353*1001 | 10. 140*1,5
| 11. 61*31 | 12. 85² |
Задания для контрольного среза №2
| 1. 36*11 | 2. 65*101 | 3. 82*88 | 4. 55² | 5. 420*1,5 | 6. 432*11
|
| 7. 86*101 | 8. 63*67 | 9. 654*1001 | 10. 360*1,5
| 11. 21*41 | 12. 95² |
Задания для контрольного среза №3
| 1. 75*11 | 2. 43*47 | 3. 44*46 | 4. 35² | 5. 648*1,5 | 6. 726*11
|
| 7. 73*101 | 8. 43*47 | 9. 863*1001 | 10. 140*1,5
| 11. 61*31 | 12. 85² |
Задания для контрольного среза №4
| 1. 15*11 | 2. 62*68 | 3. 37*33 | 4. 65² | 5. 8200*1,5 | 6. 454*11
|
| 7. 96*101 | 8. 39*31 | 9. 568*1001 | 10. 640*1,5
| 11. 81*51 | 12. 15² |
Задания для контрольного среза №5
| 1.63*11 | 2. 81*41 | 3. 56*54 | 4. 105² | 5. 860*1,5 | 6. 623*11
|
| 7. 78*101 | 8. 458*1001 | 9. 544*11 | 10. 680*1,5
| 11. 71*21 | 12. 75² |
Приложение 3
Исследовательская работа по проведению контрольных измеренийс учащимися 6-9 классов МБОУ им.Л.Н.Толстого филиала в с.Домачи
| ФИ ученика | класс | №1 t, мин | К-во пр | К-во ош | №2 t, мин | К-во пр | К-во ош | №3 t,мин | К-во прав | К-во ош | №4 t,мин | К-во прав | К-во ош | №5 t,мин | К-во пр | К-во ош |
|
|
| Нистратова Д | 6 | 10 | 8 | 4 | 8 | 10 | 2 | 5 | 12 | - | 4 | 12 | - | 2 | 12 | - |
| Тушев А | 6 | 12 | 7 | 5 | 10 | 2 | 10 | 10 | 8 | 4 | 6 | 11 | 1 | 3 | 11 | 1 |
| Кохан А | 6 | 11 | 4 | 8 | 9 | 5 | 7 | 6 | 7 | 5 | 4 | 11 | 1 | 3 | 12 | - |
| Поветьев А | 7 | 10 | 10 | 2 | 8 | 11 | 1 | 8 | 10 | 2 | 2 | 11 | 1 | 3 | 12 | - |
| Дорошин И | 7 | 10 | 8 | 4 | 8 | 7 | 5 | 5 | 12 | - | 5 | 12 | - | 4 | 12 | - |
| Котов С | 8 | 10 | 9 | 3 | 9 | 12 | - | 5 | 11 | 1 | 4 | 6 | 6 | 3 | 12 | - |
| Иноземцев Н | 8 | 12 | 10 | 2 | 10 | 11 | 1 | 9 | 12 | - | 5 | 11 | 1 | 4 | 11 | 1 |
| Ищенко Д | 9 | 10 | 9 | 3 | 5 | 12 | - | 4 | 12 | - | 2 | 12 | - | 2 | 12 | - |
| Мотылёв Д | 9 | 9 | 10 | 2 | 7 | 12 | - | 6 | 9 | 3 | 5 | 11 | 1 | 4 | 11 | 1 |
| Башлыкова Е | 9 | 12 | 8 | 4 | 10 | 8 | 4 | 12 | 12 | - | 7 | 12 | - | 3 | 12 | - |
| Колодяжный Е | 9 | 9 | 9 | 3 | 4 | 6 | 6 | 2 | 12 | - | 2 | 12 | - | 2 | 12 | - |
| Титова А | 9 | 9 | 4 | 8 | 7 | 6 | 6 | 6 | 7 | 5 | 8 | 12 | - | 4 | 12 | - |
| Средний балл(общ) |
|
| 8 |
|
| 8,5 |
|
| 10,3 |
|
| 11,1 |
|
| 11,8≈12 |
|
| Среднее время (общее) |
| 10,3 мин |
|
| 7,8 мин |
|
| 6,5 мин |
|
| 4,5 мин |
|
| 3 мин |
|
|
Приложение 4
Мониторинг времени выполнения контрольных измерений учащимися
6-9 классов МБОУ им.Л.Н.Толстого филиала в с.Домачи
Диаграмма времени по выполнению контрольных срезов
![]()
Продолжительность времени выполнения контрольных срезов
| Количество дней | время 6-7кл, мин | время 8-9 кл, мин | Общее время 6-9 кл, мин |
|
|
| 1 день | 10,6 | 10,1 | 10,4 |
| 2 день | 8,6 | 7,3 | 8,0 |
| 3день | 6,8 | 6,9 | 6,9 |
| 4 день | 4,2 | 4,7 | 4,5 |
| 5 день | 3,0 | 3,1 | 3,0 |
Приложение 5
Мониторинг правильных ответов контрольных измерений 6-9 классов МБОУ им.Л.Н.Толстого филиала в с.Домачи
Диаграмма правильных ответов контрольных срезов
![]()
Количество правильных ответов при проведении исследования
| | К-во прответов 6 класс | К-во пр ответов 7 класс | К-во пр ответов 8 класс | К-во пр ответов 9 класс | Средний балл 6-9 класс |
|
|
| 1 день | 6,3 | 9 | 9,5 | 8,0 | 8,2 |
| 2 день | 5,7 | 9 | 11,5 | 8,8 | 8,75 |
| 3 день | 9 | 11 | 11,5 | 10,4 | 10,5 |
| 4 день | 11,3 | 11,5 | 8,5 | 11,8 | 10,8 |
| 5 день | 11,7 | 12 | 11,5 | 11,8 | 11,8≈12 |
Приложение 6
Памятка устного счёта
Сложение
Основное правило для выполнения сложения в уме звучит так:
Чтобы прибавить к числу 9, прибавьте к нему 10 и отнимите 1;чтобы прибавить 8, прибавьте 10 и отнимите 2; чтобы прибавить 7, прибавьте10 и отнимите 3 и т.д. Например:
76+8=76+10-2=84;
85+9=85+10-1=94.
Сложение в уме двузначных чисел
Если цифра единиц в прибавляемом числе больше5, то число необходимо округлить в сторону увеличения, а затем вычесть ошибку округления из полученной суммы. Если же цифра единиц меньше, то прибавляем сначала десятки, а потом единицы. Например:
24+48=24+50-2=72;
28+31=28+30+1=59.
Сложение трехзначных чисел
Складываем слева на право, то есть сначала сотни, потом десятки, а затем единицы. Например:
438+325= 400+300+30+20+8+5=763;
537+196=500+100+30+90+7+6=733.
Вычитание
Чтобы вычесть два числа в уме, нужно округлить вычитаемое, а затем подкорректируйте полученный ответ.
76-9=76-10+1=67;
545-82=545-100+18=463.
Вычитание числа меньше 100 , из числа больше 100
Если вычитаемое меньше 100, а уменьшаемое больше 100, но меньше 200, есть простой способ вычислить разность в уме. 142-63=79
63 на 37 меньше 100. 142 на 42 больше 100. Прибавим 37 к 42 и получим ответ: 79.
Умножение и деление числа на 4.
Чтобы умножить число на 4, нужно его дважды умножить на 2.
Например:
32·4=(32·2)·2=64·2=128;
512·4=(512·2)·2=1024·2=2048.
Чтобы разделить число на 4, нужно его дважды разделить на 2.
Например:
828:4=(828:2):2=414:2=207.
Умножение и деление числа на 5.
Чтобы умножить число на 5, нужно его умножить на 10 и разделить на 2.
Например:
426·5=(426·10):2=4260:2=2130.
Чтобы разделить число на 5, нужно умножить 2 и разделить на 10, т.е. отделить запятой последнюю цифру.
Например:
342:5=(342·2):10=684:10=68,4.
Умножение числа на 1,5.
Чтобы умножить число на 1,5, нужно к исходному числу прибавить его половину.
Например: 120·1,5=120+60=180;
250·1,5=250+125=375.
Умножение числа на 9.
Чтобы умножить число на 9, нужно к нему приписать 0 и отнять исходное число.
Например: 65·9=650-65=585
Умножение на 25 числа, делящегося на 4.
Чтобы умножить на 25 число, делящееся на 4, нужно его разделить на 4 и получившееся число умножить на 100.
Например: 168·25=(168:4)·100=42·100=4200.
17





























