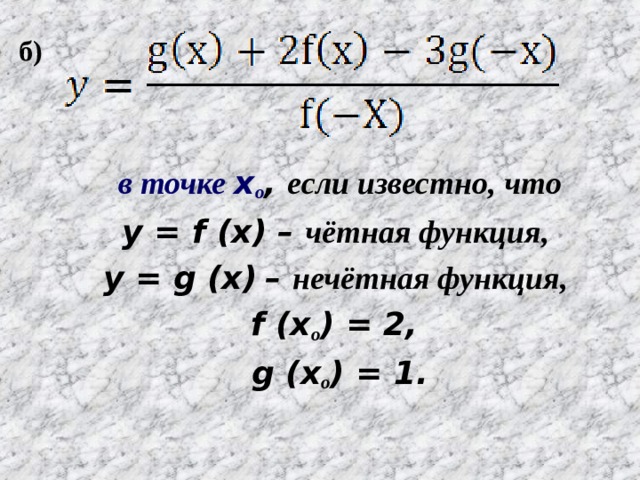В честь окончания учебного года! Скидки до 50% на готовые материалы для учителей на каждый урок

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ

Благодаря готовым учебным материалам для работы в классе и дистанционно

Выбрать материалы

Скидки до 50 % на комплекты
только до 18.06.2025

Готовые ключевые этапы урока всегда будут у вас под рукой

Организационный момент

Проверка знаний

Объяснение материала

Закрепление изученного

Итоги урока

Была в сети 21.05.2025 12:47

Попова Оксана Эдуардовна

учитель математики

37 лет

9 148

4 754

Подписчики

Подписки

Местоположение

Россия, Липецк

Специализация

Математика

Обо мне Блог Файлы Тесты Галерея Активность Награды

Четность, нечетность, периодичность функций

Категория: Алгебра

11.12.2019 23:21

Просмотр содержимого документа
«Четность, нечетность, периодичность функций»

11 класс

Функции

Чётные

Ни чётные,

ни нечётные

Нечётные

Нечётная функция

Функция y = g(x) называется нечетной , если область ее определения симметрична относительно нуля и для любого значения аргумента x верно равенство g (-x) = - g (x)

Чётная функция

Функция y = f(x) называется четной , если область ее определения симметрична относительно нуля и для любого значения аргумента x верно равенство f (-x) = f (x)

График любой четной функции симметричен относительно

оси ординат .

График любой нечетной функции симметричен относительно

начала координат .

Функцию y = f (x) , называют периодической , если существует такое отличное от нуля число T , что для любого x из множества X выполняется равенство

f (x - T) = f (x) = f (x + T) .

Число T , удовлетворяющее указанному условию, называют периодом функции

y = f (x).

Период сложной функции

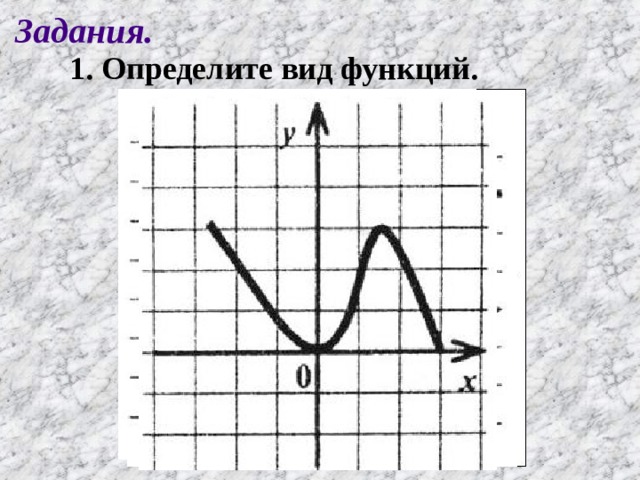
Задания.

Определите вид функций.

2. Дан фрагмент графика четной функции f(х), которая

определена на [–9; 9]. Достройте график функции f(х) и ответьте на следующие вопросы:

Сколько нулей функции на этом промежутке?
Сколько промежутков возрастания и убывания?
Сколько промежутков, на которых значения функции

положительны (отрицательны)?

Выполните это же задание, учитывая, что теперь дан

фрагмент нечетной функции.

3. Проверьте , является ли четной или нечетной функция, заданная формулой:

f ( х ) = 2 х ³ + 8 х f ( х ) = 0,5 х ² + 3 х + 5

g ( х ) = – 5 х ² + 5 х ³ g ( х ) = 6 х – 29 х ³ + 3 х ²

f ( х ) = 2 х ³ – 3 х ² f ( х ) = 5 х ² + 3 х ²

g ( х ) = – х ² + 5 х ² g ( х ) = –2 х ³ + 3 х ³

4. Найдите значение функции f (9) , если известно, что функция y = f (x) – чётная , имеет период 10 и на отрезке [0 ;5 ] функция имеет вид y = 15 + 2x - x 2

5. Четная функция y = f (x) определена на всей числовой прямой. Для всякого неотрицательного значения переменной x значение этой функции совпадает со значением функции g (x) = 13x(2x+1)(7x+6)(4x-9).

Сколько корней имеет уравнение f (x) =0 ?

6. Найдите значения функций

а)

y =

если известно, что функция y = f (x) - нечётная, функция y = g (x) – чётная, f (a) = 2, g (a) = -5.

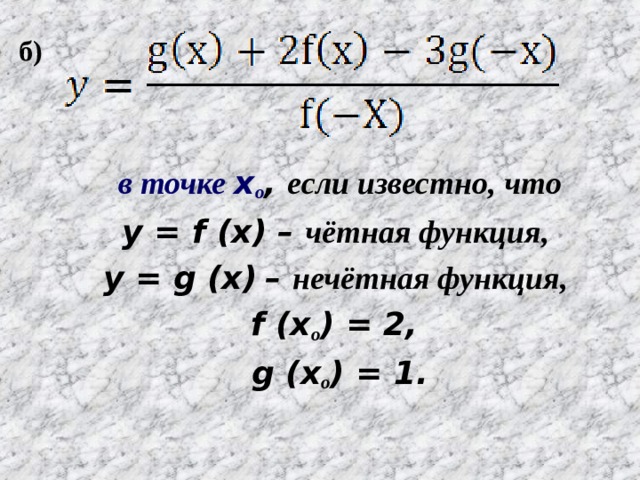
в точке x ο , если известно, что

y = f (x) – чётная функция,

y = g (x) – нечётная функция,

f (x ο ) = 2,

g (x ο ) = 1.

б)

7. Для чётной функции f (x) и нечётной функции g (x) для всех действительных значений аргумента выполнено равенство

f (x) + g (x) = 2x² - 7x - 5 .

Найдите корень

(или сумму корней, если их несколько) уравнения f (x) = g (x).

8. Периодическая функция y = f (x) определена для всех действительных чисел. Её период равен 4 и f (3) = 8. Найдите значение выражения

7 f(15) – 2f(-1) – 4f(-17) .

9. Периодическая функция y = f (x) определена на всей числовой оси. Её период равен 3. На промежутке [-2;1) значения функции y = f (x) совпадают со значениями функции

Вычислите f (11) .