Численные методы в алгебре

Лекция 3:

Численные методы линейной алгебры.

Методы решений нелинейных уравнений и систем.

К численным методам линейной алгебры относятся численные

методы решения систем линейных алгебраических уравнений, обращение

матриц, вычисление определителей, нахождение собственных значений и

собственных векторов матриц. Численные методы решения систем линейных

алгебраических уравнений разделяются на две группы:

• Точные или прямые методы , которые позволяют найти решение

системы линейных алгебраических уравнений за конечное число

арифметических действий. Сюда относятся метод Крамера (нахождение

решения систем с помощью определителей), метод Гаусса, метод

прогонки.

• Приближенные методы. В частности итерационные методы решения

систем алгебраических уравнений.

Правило Крамера в вычислительной математике с использованием ЭВМ не

применяется, т.к. оно требует использования большого числа операций и

объемов памяти. Метод Гаусса используется для решения СЛАУ размерности .

Итерационными методами решаются системы размерностью .

Методом прогонки решаются системы линейных алгебраических уравнений

специального вида, содержащие трехдиагональные матрицы.

П.1 Метод простой итерации.

Рассмотрим систему линейных алгебраических уравнений n – го

порядка, записанную в виде:

(3.1) ,

где - квадратичная числовая матрица n – порядка.

- n – мерный вектор, неизвестная величина, которую требуется найти.

- n – мерный вектор (известный, заданный столбец свободных членов).

Задав начальное приближение, итерационный процесс

нахождения приближенного решения (3.1) сформулируем следующим

образом:

(3.2)

Выясним, при каких условиях на матрицу , решение найденное по методу

простой итерации будет сходиться к решению задачи (3.1).

Практическая схема решения СЛАУ методом простой итерации

Рассмотрим для простоты систему, состоящую из трёх уравнений с тремя

неизвестными:

1). Преобразуем эту систему к системе вида:

(3.3)

где

(3.4)

Этого можно добиться:

• переставляя столбцы исходной системы ;
• меняя строки ;
• делая линейную комбинацию из строк.

2) из первого уравнения (3.3) выразим ;

из второго уравнения (3.3) выразим ;

из третьего уравнения (3.3) выразим ;

Получим:

Правая часть этой системы имеет нормальную матрицу

Учитывая (3.4) и обозначив через – точное решение, а через

– n – тую итерацию, будем иметь

Найдя с помощью вышеуказанного равенства, а также , выясним при

каком номере N будет выполняться неравенство:

Метод нахождения на n – й итерации имеет вид:

В процессе выполнения этого итерационного процесса, на каждом шаге

находим разность . Когда

выполнение итерационного процесса прекращаем, решение найдено с

заданной точностью.

3) На практике часто используется итерационный процесс Гаусса – Зейделя,

который имеет вид:

(3.5)

Выясним при каких условиях сходится метод Гаусса – Зейделя.

Теорема 3.1: Для того, чтобы решение по методу Гаусса – Зейделя

существовало и было единственно, и для того, чтобы итерационный процесс

(3.5) сходился, достаточно выполнение условий (3.4).

Методы решений нелинейных уравнений и систем п.1 Задача отделения корней

Пусть требуется решить уравнение с одной неизвестной: , где

- заданная функция.

Задача определения корней для уравнения

(3.6) f( x )=0

состоит в определении отрезков, которые содержат один и

только один корень этого уравнения.

Теорема 3.2: Пусть ф. , f ( a ) f ( b )

концах значения разного знака, кроме того не меняет знак на [ a , b ],

тогда уравнение (3.6) имеет единственное решение на [ a , b ].

Док-во: Т.к. ф. f( x ) непрерывна на [ a , b ] и при х=а, x =b принимает значения

разного знака, то f ( x ) пересекает ось Ох хотя бы один раз, т.е. решение

уравнения (3.6) существует.

Единственность решения следует из того, что вторая производная не

меняет знак на [ a , b ]. Убедимся в этом из геометрических соображений.

П.2. Метод Ньютона (метод касательных )

Пусть , f ( a )  f ( b )

меняет знак на [ a , b ].

– функция,

задающая касательную.

Y=0, найдём точку , точку пересечения

этой касательной с О x.

В общем случае формула в методе Ньютона записывается:

Замечание: В качестве в методе

Ньютона выбирается тот конец отрезка

[ a , b ], в котором знак функции совпадает со

знаком второй производной этой функции

в этой точке.

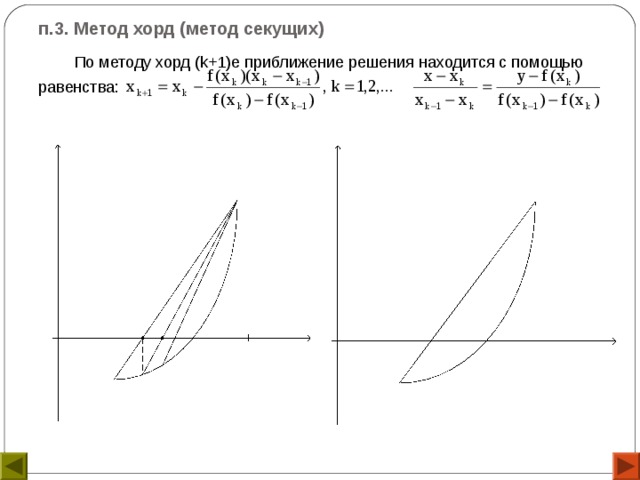
п.3. Метод хорд (метод секущих)

По методу хорд ( k +1)е приближение решения находится с помощью

равенства:

П.4 Комбинированный метод

При использовании методов Ньютона и секущих мы приближаемся к

точному решению с одной стороны.

Комбинированный способ состоит в попеременном применении метода

Ньютона и секущих, тогда приближение идет с двух сторон. При

комбинированном методе приближение начинают делать с метода

касательных.

Точность вычислений.

Пусть требуется решать уравнение (3.6) с точностью ε.

ε=

При использовании комбинированного метода точность приближения

определяется формулой

В качестве корня выбирается:

п.5. Метод итераций

Пусть требуется решить уравнение

(3.7) , которое может не иметь решения, иметь одно решение или

иметь бесконечное множество решений.

Сформулируем теорему, которая дает достаточное условие, при котором

это уравнение имеет единственное решение и укажем итерационный

процесс для нахождения приближенного решения этого уравнения.

Определение 3.1: Будем говорить, что ф. f ( x ) на [ a , b ] удовлетворяет

условию Липшица с постоянной α, если будет справедливо

неравенство:

(3.8)

Теорема 3.3: ] ф. на удовлетворяет условию Липшица

с постоянной , тогда уравнение

имеет единственное решение , причем , где ,

при этом имеют место оценки:

Литература

Е.А. Волков Численные методы, М. Наука, 1987 (либо последующие издания):

& 4-12, 15, 19-22, 24,25, 29-33.