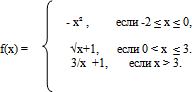Урок №1
Тема: " Числовая функция ”.
Цель:
Образовательные: ввести понятие числовой функции; научить строить кусочно-заданную функцию, функцию дробной части числа, функцию целой части числа.
Развивающие: развивать мышление и математическое представление;
Воспитательные: воспитать аккуратность в построении графиков;
Ход урока
1. Организационный момент. (2 мин)
2. Повторение материала 9 класса (10мин)
В различных сферах жизни мы нередко имеем дело со всевозможными соответствиями, т.е. правилами, по которым одним объектам (элементам) сопоставляются другие. Вот некоторые примеры таких соответствий.

Все эти соответствия можно разделить на группы по различным признакам. Но, есть среди них совершенно особенные, такие как 1, 2 и 5. Это такие соответствия, при которых каждому элементу одного множества сопоставляется единственный элемент другого множества. Такие соответствия и называются функциями.
3. Изучение нового материала(10мин)
| Задания и вопросы учителя | Предполагаемые ответы учащихся |
| Что же такое функция? | Определение 1. Если даны числовое множество Х и правило f , позволяющее поставить в соответствие каждому элементу х из множества Х определенное число у, то говорят, что задана функция у = f (х) с областью определения Х. |
| Как записывают? | Пишут : у = f(х), х Є Х. |
| Как обозначают область определения? | Для области определения функции используют обозначение D (f). |
| Как обозначают множество значений? | Множество всех значений функции у = f (x) называют областью значений функции и обозначают E (f). |
| Как называют переменную х ? | Х – независимая переменная или аргумент. |
| Как называют переменную у ? | У – зависимая переменная. |
| Найдите область определения функций: ![]() у = √х у = √х у = х² у = х / (х+2) ![]() у= (5-3х)/(√х+3 ) | D (f) = [ 0; ∞) D (f) = (-∞; +∞) D (f) = (-∞; -2)∩(-2; +∞) D (f) =( -3; +∞) |
| Вычислите значения данных функций в точках 1 и 4. | х=1, у=1
х=4, у=2 х=1, у=1
х=4, у=16 х=1, у=1/3
х=4, у=2/3  х=1, у=1 х=1, у=1
х=4, у=-7/√7
|
| Что такое график функции? | Определение 2. Если дана функция у = f(x) , хЄХ и на координатной плоскости хОу отмечены все точки вида (х; у), где х Є Х, а у = f (x), то множество этих точек называют графиком функции. |
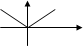
| Как выглядят графики некоторых функций? |
у = kx+m
y = ax² +bx +c
y = k/x
y = √x
y = IxI | у = kx+m – прямая
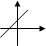 у = ax² +bx +c – парабола
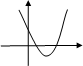 у = к/х – гипербола
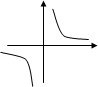 у = √х
 у = IхI
 |
4. Закрепление изученного. (13мин)
Дана функция у = f(х), где
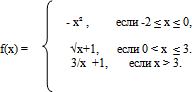
Вычислить:
а) f( -2); в) f( 1, 25);
б) f ( 0); г) f(6).
Найти D (f) и E(f).
Выяснить, сколько корней имеет уравнение f(х) =а при различных значениях а.
Решить неравенства:
а) f(х) б) f(х) 0,5.
Решение.
Дана кусочная функция.
1.
а) значение х=-2 удовлетворяет условию -2 ≤ х ≤ 0, значит f( -2) надо вычислять по формуле f(х) =- х²; f( -2) = -(-2)² =-4.
б) значение х =0 удовлетворяет условию -2 ≤ х ≤ 0, значит f ( 0) надо вычислять по формуле f(х) =- х²; f ( 0) =-0² =0.
в) значение f( 1, 25) удовлетворяет условию 0
г) значение f(6) удовлетворяет условию х 3, значит f(6) надо вычислять по формуле 3/х +1
f(6)=3:х +1= 3:6+1=1,5.
2. Область определения D (f) состоит из трех промежутков: [-2;0], (0;3], (3; +∞). Объединив их, получим луч [-2; +∞).
Чтобы найти область значений функции, построим ее график. Он состоит из трех кусочков заданной функции. Спроецировав этот график на ось у, получим область значений функции.
E(f)= [-4; 0]U( 1; 2]
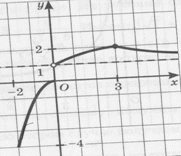
3. Выясним, сколько корней имеет уравнение f(х) =а при различных значениях а.
Для этого нужно определить, сколько точек пересечения имеет построенный график функции с прямой у=а при различных значениях параметра а.
При -4 ≤ а≤ 0 прямая пересекается с графиком в одной точке. Значит, уравнение имеет 1 корень.
При а
При 0
При а2 корней нет.
При а=2 – 1 корень.
При 1
4. Решим неравенство f(х)
f(х) 0,5 при х 0.
5. Итог урока.(5мин)
6.Домашнее задание.(5мин) §1. № 1.1 (в,г); 1.3(а,б); 1.4 (в,г); 1.6; 1.7
Урок №2
Тема: «Свойства функции»
Цель:
Образовательные: рассмотреть основные свойства функции;
Развивающие: содействовать развитию внимания;
Воспитательные: формировать ответственность;
.
Ход урока
1. Организационный момент. (2 мин)
2. Проверка домашнего задания(5мин)
Ответы на вопросы по домашнему заданию
3. Изучение нового материала(15мин)
Четко сформулируем основные свойства функции, на которые необходимо обращать внимание при исследовании функций и построении их графиков.
Основные свойства функций.
1. Область определения функции.
Область определения функции D(y)-это множество всех допустимых значений аргумента x ( независимой переменной x), при которых выражение, стоящее в правой части уравнения функции  имеет смысл. Другими словами, это область допустимых значений выражения
имеет смысл. Другими словами, это область допустимых значений выражения 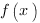 .
.
Чтобы по графику функции  найти ее область определения, нужно, двигаясь слева направо вдоль оси ОХ, записать все промежутки значений х, на которых существует график функции.
найти ее область определения, нужно, двигаясь слева направо вдоль оси ОХ, записать все промежутки значений х, на которых существует график функции.
2. Множество значений функции.
Множество значений функции Е(y)- это множество всех значений, которые может принимать зависимая переменная y.
Чтобы по графику функции  найти ее множество значений, нужно, двигаясь снизу вверх вдоль оси OY, записать все промежутки значений y, на которых существует график функции.
найти ее множество значений, нужно, двигаясь снизу вверх вдоль оси OY, записать все промежутки значений y, на которых существует график функции.
3. Нули функции.
Нули функции – это те значения аргумента х, при которых значение функции (y) равно нулю.
Чтобы найти нули функции  , нужно решить уравнение
, нужно решить уравнение 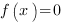 . Корни этого уравнения и будут нулями функции
. Корни этого уравнения и будут нулями функции  .
.
Чтобы найти нули функции  по ее графику, нужно найти точки пересечения графика с осью ОХ. Абсциссы точек пересечения и будут нулями функции
по ее графику, нужно найти точки пересечения графика с осью ОХ. Абсциссы точек пересечения и будут нулями функции  .
.
4. Промежутки знакопостоянства функции.
Промежутки знакопостоянства функции  – это такие промежутки значений аргумента, на которых функция сохраняет свой знак, то есть
– это такие промежутки значений аргумента, на которых функция сохраняет свой знак, то есть 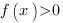 или
или 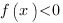 .
.
Чтобы найти промежутки знакопостоянства функции  , нужно решить неравенства
, нужно решить неравенства 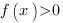 и
и 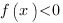 .
.
Чтобы найти промежутки знакопостоянства функции  по ее графику, нужно
по ее графику, нужно
найти промежутки значений аргумента х, при которых график функции расположен выше оси ОХ – при этих значениях аргумента 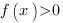
найти промежутки значений аргумента х, при которых график функции расположен ниже оси ОХ – при этих значениях аргумента 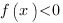
5. Промежутки монотонности функции.
Промежутки монотонности функции  – это такие промежутки значений аргумента х, при которых функция
– это такие промежутки значений аргумента х, при которых функция  возрастает или убывает.
возрастает или убывает.
Говорят, что функция  возрастает на промежутке I, если для любых двух значений аргумента
возрастает на промежутке I, если для любых двух значений аргумента  , принадлежащих промежутку I таких, что
, принадлежащих промежутку I таких, что  выполняется соотношение: .
выполняется соотношение: .
Другими словами, функция  возрастает на промежутке I, если большему значению аргумента из этого промежутка соответствует большее значение функции.
возрастает на промежутке I, если большему значению аргумента из этого промежутка соответствует большее значение функции.
Чтобы по графику функции  определить промежутки возрастания функции, нужно, двигаясь слева направо по линии графика функции, выделить промежутки значений аргумента х, на которыхграфик идет вверх.
определить промежутки возрастания функции, нужно, двигаясь слева направо по линии графика функции, выделить промежутки значений аргумента х, на которыхграфик идет вверх.
Говорят, что функция  убывает на промежутке I, если для любых двух значений аргумента
убывает на промежутке I, если для любых двух значений аргумента  , принадлежащих промежутку I таких, что
, принадлежащих промежутку I таких, что  выполняется соотношение: .
выполняется соотношение: .
Другими словами, функция  убывает на промежутке I, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.
убывает на промежутке I, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.
Чтобы по графику функции  определить промежутки убывания функции, нужно, двигаясь слева направо вдоль линии графика функции, выделить промежутки значений аргумента х, на которыхграфик идет вниз.
определить промежутки убывания функции, нужно, двигаясь слева направо вдоль линии графика функции, выделить промежутки значений аргумента х, на которыхграфик идет вниз.
6. Точки максимума и минимума функции.
Точка  называется точкой максимума функции
называется точкой максимума функции  , если существует такая окрестность I точки
, если существует такая окрестность I точки  , что для любой точки х из этой окрестности выполняется соотношение:
, что для любой точки х из этой окрестности выполняется соотношение:
Графически это означает что точка с абсциссой  лежит выше других точек из окрестности I графика функции
лежит выше других точек из окрестности I графика функции  .
.
Точка  называется точкой минимума функции
называется точкой минимума функции  , если существует такая окрестность I точки
, если существует такая окрестность I точки  , что для любой точки х из этой окрестности выполняется соотношение:
, что для любой точки х из этой окрестности выполняется соотношение:

Графически это означает что точка с абсциссой  лежит ниже других точек из окрестности I графика функции
лежит ниже других точек из окрестности I графика функции  .
.
Обычно мы находим точки максимума и минимума функции, проводя исследование функции с помощью производной.
7. Четность (нечетность) функции.
Функция  называется четной, если выполняются два условия:
называется четной, если выполняются два условия:
а) Для любого значения аргумента  , принадлежащего области определения функции,
, принадлежащего области определения функции,  также принадлежит области определения функции.
также принадлежит области определения функции.
Другими словами, область определения четной функции  симметрична относительно начала координат.
симметрична относительно начала координат.
б) Для любого значения аргумента х, принадлежащего области определения функции, выполняется соотношение  .
.
Функция  называется нечетной, если выполняются два условия:
называется нечетной, если выполняются два условия:
а) Для любого значения аргумента  , принадлежащего области определения функции,
, принадлежащего области определения функции,  также принадлежит области определения функции.
также принадлежит области определения функции.
Другими словами, область определения нечетной функции  симметрична относительно начала координат.
симметрична относительно начала координат.
б) Для любого значения аргумента х, принадлежащего области определения функции, выполняется соотношение .
Все функции делятся на четные, нечетные, и те, которые не являются четными и не являются нечетными. Они называются функциями общего вида.
Чтобы определить четность функции, нужно:
а). Найти область определения функции  , и определить, является ли она симметричным множеством.
, и определить, является ли она симметричным множеством.
Если, например, число х=2 входит в область определения функции, а число х=-2 не входит, то D(y) не является симметричным множеством, и функция  – функция общего вида.
– функция общего вида.
Если область определения функции  – симметричное множество, то проверяем п. б)
– симметричное множество, то проверяем п. б)
б). В уравнение функции  нужно вместо х подставить -х, упростить полученное выражение, и постараться привести его к виду
нужно вместо х подставить -х, упростить полученное выражение, и постараться привести его к виду 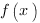 или
или  .
.
Если  , то функция четная.
, то функция четная.
Если , то функция нечетная.
Если не удалось привести ни к тому ни к другому, то наша функция  – общего вида.
– общего вида.
График четной функции симметричен относительно оси ординат ( прямой OY ).
График нечетной функции симметричен относительно начала координат ( точки (0,0) ).
8. Периодичность функции.
Функция  называется периодической, если существует такое положительное число Т, что
называется периодической, если существует такое положительное число Т, что
В программе средней школы из числа периодических функций изучают только тригонометрические функции.
4.Решение примеров(17мин)
5. Итог урока.(3мин)
6.Домашнее задание.(3мин)







 х=1, у=1
х=1, у=1