МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД
МКОУ «НОВОМАКИНСКАЯ СОШ»

 НА ТЕМУ:
НА ТЕМУ:
![]()

Подготовил: учитель математики
Тагирбеков Л.Т.
с.Новая Мака
2019 г.
История чисел.
Цифры – одно из древнейших изобретений. Из цифр складываются числа: маленькие, большие и очень большие.
Но всегда ли было так?
Во все ли времена и у всех ли народов?
Сначала считали на пальцах
Не так уж и много приходилось считать первобытному человеку. Был у него свой первобытный «компьютер» - десять пальцев на руках. Разгибал пальцы, складывал числа. Загибал – вычитал. На пальцах считать удобно, только результат счета хранить нельзя. Не станешь же целый день ходить с загнутыми пальцами. Этот древний «прибор» и сейчас используют маленькие дети, когда начинают учиться считать в пределах десяти. Сначала считали на пальцах. Когда пальцы на одной руке кончались, переходили на другую, а если на двух руках не хватало, переходили на ноги. Поэтому, если в те времена кто-то хвалился, что у него «две руки и одна нога кур», это означало, что у него пятнадцать кур, а если это называлось «весь человек», то есть две руки и две ноги.
Ещё недавно существовали племена, в языке которых были названия только двух чисел: «один» и «два». Пять — рука, шесть — один на другой руке, семь — два на другой руке, десять — две руки, полчеловека. Пятнадцать — нога, шестнадцать — один на другой ноге, двадцать — один человек, двадцать два — два на руке другого человека, сорок — два человека, пятьдесят три — три на первой ноге у третьего человека. Раньше люди чтобы пересчитать стадо из 128 оленей должны были взять семь человек.
Использование камней, узелков.
Древний человек догадался: для счета можно использовать не только пальцы, но и все, что попадается под руки – камешки, палочки, косточки... В древние времена, когда человек хотел показать, сколькими животными он владел, он клал в большой мешок столько камешков, сколько у него было животных. Чем больше животных, тем больше камешков. Отсюда и произошло слово «калькулятор», «калькулюс» по латински означает «камень».
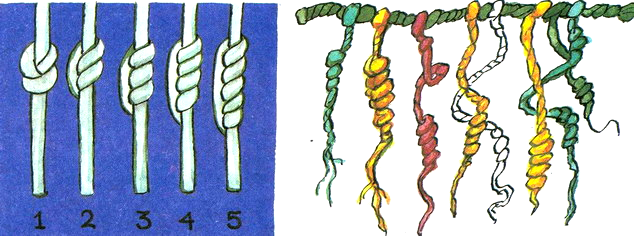
Перуанские инки вели счет животных и урожая, завязывая узелки на ремешках или шнурках разной длины и цвета .Эти узелки назывались кипу. У некоторых богатеев скапливалось по несколько метров этой веревочной «счетной книги», попробуй, вспомни через год, что означают 4 узелочка на шнурочке! Поэтому того, кто завязывал узелки, называли вспоминателем.
Древние шумеры
Первыми придумали запись чисел древние шумеры. Они пользовались всего двумя цифрами. Вертикальная чёрточка обозначала одну единицу, а угол из двух лежачих чёрточек – десять. Эти чёрточки у них получались в виде клиньев, потому что они писали острой палочкой на сырых глиняных дощечках, которые потом сушили и обжигали. Вот так выглядели эти дощечки .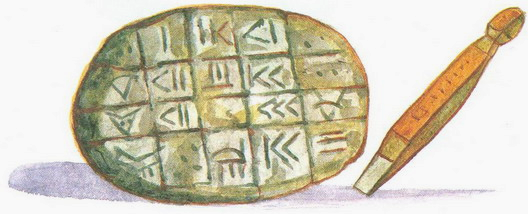
После счета по зарубкам люди изобрели особые символы, названные цифрами. Они стали применяться для обозначения различных количеств каких-либо предметов. Разные цивилизации создавали свои собственные цифры
Египетская нумерология
Так, например, в древней египетской нумерации, зародившейся более 5000 лет назад, существовали особые знаки (иероглифы) для записи чисел 1, 10, 100, 1000, …:
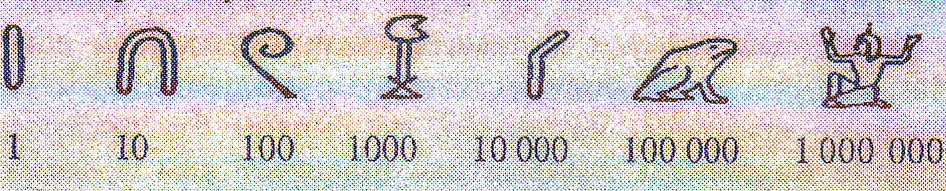
Для того чтобы изобразить, например, целое число 23145, достаточно записать в ряд два иероглифа, изображающие десять тысяч, затем три иероглифа для тысячи, один – для ста, четыре – для десяти и пять иероглифов для единицы:
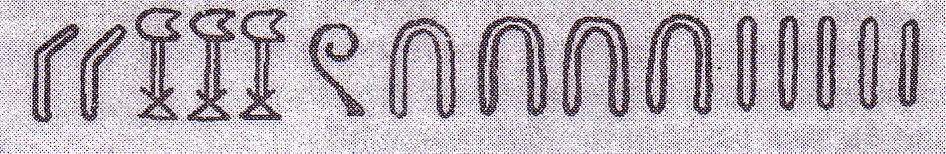
Этого одного примера достаточно, чтобы научиться записывать числа так, как их изображали древние египтяне. Это система очень проста и примитивна.
Народы (вавилоняне, ассирийцы, шумеры), жившие в Междуречье Тигра и Евфрата в период от II тысячелетия до н.э. до начала нашей эры,
сначала обозначали числа с помощью кругов и полукругов различной величины, но затем стали использовать только два клинописных знака – прямой клин и лежащий клин . Эти народы использовали шестидесятеричную систему счисления, например число 23 изображали так: . Число 60 снова обозначалось знаком , например число 92 записывали так: .
Индейцы племени майя
В начале нашей эры индейцы племени майя, которые жили на полуострове Юкатан в Центральной Америке, пользовались другой системой счисления – двадцатеричной. Они обозначали 1 точкой, а 5 – горизонтальной чертой, например, запись ‗‗‗‗‗‗ означала 14. В системе счисления майя был и знак для нуля. По своей форме он напоминал полузакрытый глаз.
В Древней Греции
Сначала числа 5, 10, 100, 1000, 10000 обозначали буквами Г, Н, Х, М, а число 1 – черточкой /. Из этих знаков составляли обозначения Г (35) и т.д. Позднее числа 1, 2, 3, 4, 5, 6, 7, 8, …стали обозначать буквами греческого алфавита, к которому пришлось добавить еще три устаревшие буквы. Чтобы отличить цифры от букв, над буквами ставили черточку.
Древние индийцы
изобрели для каждой цифры свой знак. Вот как они выглядели
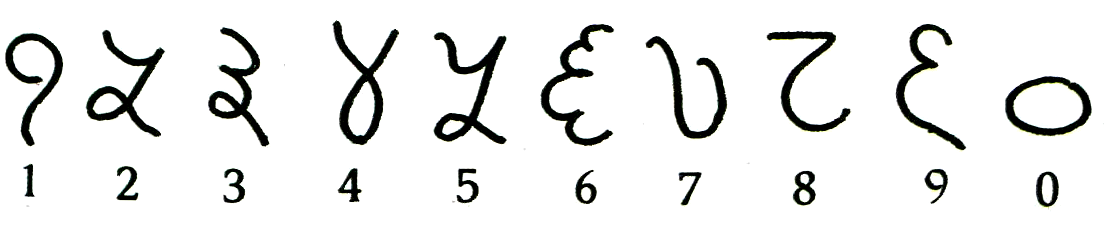
Однако Индия была оторвана от других стран, - на пути лежали тысячи километров расстояния и высокие горы.
Арабы были первыми «чужими», которые заимствовали цифры у индийцев и привезли их в Европу. Чуть позже арабы упростили эти значки, они стали выглядеть вот так
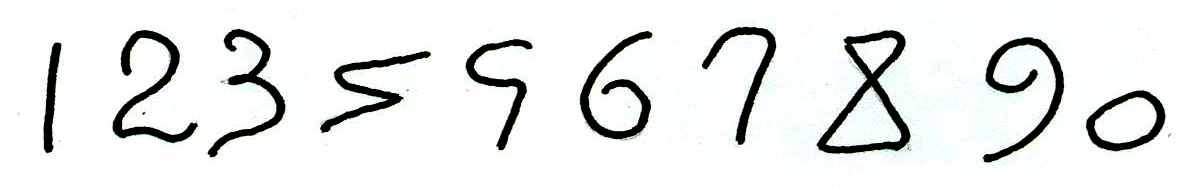
Они похожи на многие наши цифры. Слово «цифра» тоже досталось нам от арабов по наследству. Арабы нуль, или «пусто», называли «сифра». С тех пор и появилось слово «цифра».
Римская нумерация.
В основе римской нумерации использованы принципы сложения (например, VI = V + I) и вычитания (например, IX = X -1). Римская система нумерации десятичная, но непозиционная. Римские цифры произошли не от букв. Первоначально они обозначались, как и у многих народов, «палочками» (I - один, X - 10 - перечеркнутая палочка, V - 5 - половина от десяти, сто - кружочек с черточкой внутри, пятьдесят — половина этого знака и т. д.).
Со временем некоторые знаки изменились: С - сто, L - пятьдесят, М - тысяча, D - пятьсот. Например:
XL - 40, LXXX - 80, ХС - 90,
CDLIX - 459, CCCLXXXII - 382,
CMXCI - 991, MCMXCVIII - 1998, MMI – 2001

Произошло постепенное превращение первоначальных цифр в наши современные цифры.
Цифры русского народа.
Арабские числа в России стали применять, в основном, с XVIII века. До того наши предки использовали славянскую нумерацию. Над буквами ставились титлы (черточки), и тогда буквы обозначали числа. В одной из русских рукописей XVIII века написано: «... Знай же то, что есть сто и что есть тысяща, и что есть тма, и что есть легион, и что есть леодр...; ... сто есть десятью десять, а тысяща есть десять сот, а тма десять тысящ, а легион есть десять тем, а леодр есть десять легионов...». Сотни миллионов назывались «колодами». Первые девять чисел записывались так:
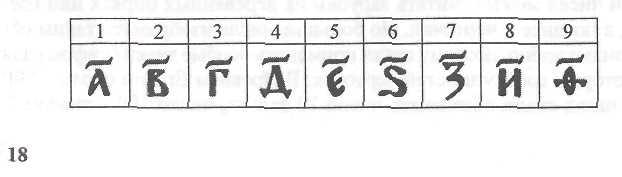
В первой части своей работы я рассказала этапы развития чисел - от первобытного строя до современности.
Натуральные числа
Исторически первыми возникли натуральные числа N, как результат пересчета пердметов. Множество этих чисел бесконечно и образует натуральный ряд N={1,2,3,...,n,...}. В этом множестве выполнимы операции сложения и умножения. Для выполнения операции вычитания потребовались новые числа, что привело к появлению множества целых чисел: Z. Z=N+∪N−∪{0}. Таким образом в множестве целых чисел всегда выполняются операции сложения, умножения, вычитания.
Рациональные числа
Необходимость выполнения деления привела к множеству рациональных чисел Q. Q={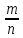 ,m∈Z,n∈N}.
,m∈Z,n∈N}.
Определение. Два рациональных числа равны: 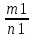 =
=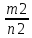 - если m1⋅n2=n1⋅m2. Это означает, что всякое рациональное число можно представить единственным образом в виде несократмой дроби
- если m1⋅n2=n1⋅m2. Это означает, что всякое рациональное число можно представить единственным образом в виде несократмой дроби 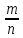 . НОД(m,n)=1.
. НОД(m,n)=1.
Свойства множества рациональных чисел
1. В результате арифметических операций над рациональными числами (сложение, умножение, вычитание, деление, кроме деления на ноль) получается рациональное число.
2. Множество рациональных чисел упорядочено, то есть для любой пары рациональных чисел a и b либо ab, либо ab.
3. Множество рациональных чисел плотно, то есть для любой пары рациональных чисел a и b существует такое рациональное число c, что abc. Очевидно, что таких чисел бесконечное множество.
Всякое положительное рациональное число всегда можно представить в виде десятичной дроби: либо конечной, либо бесконечной периодической. Например: 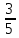 =0,6,
=0,6, 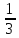 =0,333...=0,(3).
=0,333...=0,(3).
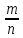 =a0,a1a1...akb1b2b3...bnb1b2b3...bn....
=a0,a1a1...akb1b2b3...bnb1b2b3...bn....
b1b2b3...bn... - называется периодом десятичной дроби, где не все bi=0.
Заметим, что конечная дробь может быть записана в виде бесконечной периодической с нулем в периоде. 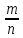 =a0,a1a1...ak000000..., ak≠0.
=a0,a1a1...ak000000..., ak≠0.
Однако, чаще встречается другое представление рациональных чисел в виде десятичной дроби: 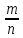 =a0,a1a1...(ak−1)999....
=a0,a1a1...(ak−1)999....
Отрицательные рациональные числа −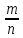 записываютсяв виде десятичного разложения рационального числа вида
записываютсяв виде десятичного разложения рационального числа вида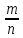 , взятого с противоположным знаком.
, взятого с противоположным знаком.
Число 0 представляется в виде 0,000....
Таким образом, всякое рациональное число всегда представимо в виде бесконечной десятичной периодической дроби не содержащей 0 в периоде, кроме самого числа 0. Такое представление единственное.
Иррациональные числа
Множество рациональных чисел замкнуто относительно четырёх арифметических операций. Однако в множестве рациональных чисел не всегда имеет место решение простейшего уравнения вида x2−n=0. Поэтому возникает необходимость введения новых чисел.
Покажем, что среди рациональных чисел нет числа, квадрат которого равен трём. Доказательство проведём методом от противного.
Предположим, что существует рациональное число 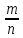 такое, что его квадрат равен трём: (
такое, что его квадрат равен трём: (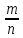 )2=3(1).
)2=3(1).
Будем считать дробь 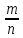 несократимой.
несократимой.
 =3
=3
m2=3n2.(2)
Правая часть равенства (2) делится на 3. Значит и m2 делится на 3, следовательно m делится на 3, а это значит, что m=3k. Подставим в равенство (2), получим:
9k2=3n2,
3k2=n2.(3)
Левая часть равенства (3) делится на 3, значит и правая часть делится на 3. Следовательно n2 делится на 3, значит и n делится на 3, откуда n=3p. В результате получаем: 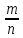 =
= , то есть дробь
, то есть дробь 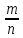 оказалась сократимой, что противоречит предположению. Значит, среди рациональных чисел нет такого числа, квадрат которого равен трём.
оказалась сократимой, что противоречит предположению. Значит, среди рациональных чисел нет такого числа, квадрат которого равен трём.
Но число, квадрат которого равен трём, существует. Оно представимо в виде бесконечной непериодической дроби. И мы получили новый вид чисел. Назовём их иррациональными.
Определение. Иррациональным числом называется любая бесконечная непериодическая дробь.
Множество всех бесконечных непериодических дробей называется множеством иррациональных чисел и обозначается I.
Действительные числа
Объединение множества рациональных чисел Q и иррациональных чисел I даёт множество действительных чисел R: Q∪I=R.
Множество действительных чисел
Таким образом всякое действительное число представимо в виде бесконечной десятичной дроби: периодической в случае рационального числа и непериодической в случае иррационального числа.
Сравнение действительных чисел
Для действительных чисел a=a0,a1a2a3…an…, b=b0,b1b2b3…bn… сравнение осуществляется следующим образом:
1) Пусть a и b оба положительны: a0, b0, тогда:
a=b, если для любого k ak=bk;
ab, если ∃s ∀kk=bk, asbs.
2) Пусть a0, bba, следовательно ba.
3) Пусть a и b оба отрицательны: ab
a=b, если для −a=−b;
ab, если −ab.
Проследив основные этапы зарождения чисел, их различных систем записей у разных народов, необходимо сделать такой вывод: не зря многие ученые умы интересовались понятием числа, раскрывали его тайны. Да и в наш технократичный век, когда с числами сталкиваешься повсеместно (на денежных знаках, ценниках, компьютерах, панелях стиральных машин и т.д.) это понятие не утратило своей актуальности. Трудно себе представить как современный человек смог бы прожить, если бы когда-то, много тысячелетий назад, не была бы приоткрыта тайна великих и загадочных чисел.
Литература.
Акимова С. Занимательная математика. – СПб.; Тригон, 1997.
Дектярёва З. А. Математика после уроков. - Краснодар, 1996.
Депман И. Я. За страницами учебника математики. – М.; Просвещение,1989.
Математика: Школьная энциклопедия. – М.; «Большая Российская энциклопедия», 1996.
Мясникова Т. История развития понятия отрицательного числа. – М., Первое сентября. – 2004. - № 41.
Позднякова А. Г. Математический вечер в школе. / Математика в школе. – 1989. - № 5.
Трифонов Д. Математические силуэты «звериного» числа. / Математика – 1999. - № 1.
Шеина О. С., Соловьёва Г. М. Математика. Занятие школьного кружка. 5 – 6 класс. – М., НЦ ЭНАС, 2001.
Щербакова Ю. В. Занимательная математика на уроках и внеклассных мероприятиях. 5 – 8 классы. – М.; ООО «Глобус», 2008.
10. Я познаю мир: Детская энциклопедия: Математика./ Под ред. О. Г. Хини. – М.; АСТ – ЛТД, 1997.







 НА ТЕМУ:
НА ТЕМУ:


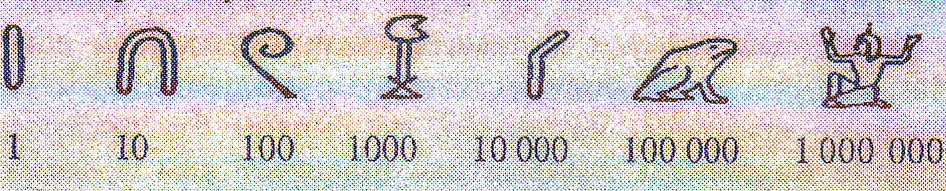
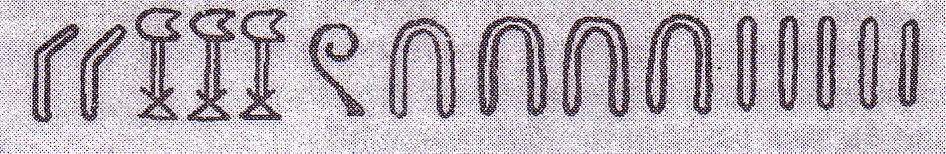
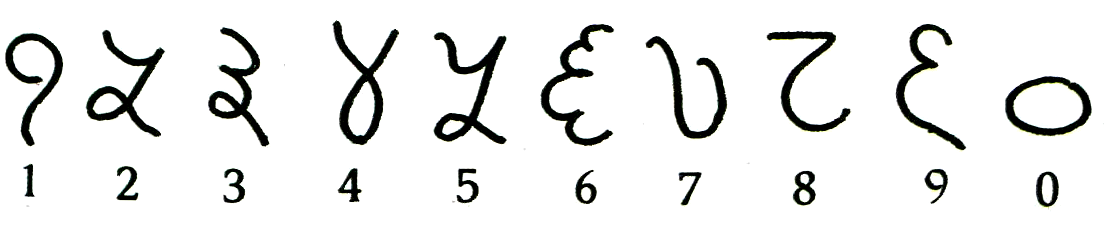


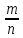 ,m∈Z,n∈N}.
,m∈Z,n∈N}.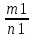 =
=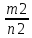 - если m1⋅n2=n1⋅m2. Это означает, что всякое рациональное число можно представить единственным образом в виде несократмой дроби
- если m1⋅n2=n1⋅m2. Это означает, что всякое рациональное число можно представить единственным образом в виде несократмой дроби 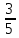 =0,6,
=0,6, 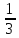 =0,333...=0,(3).
=0,333...=0,(3).









