Сабирзянова Светлана Владимировна, учитель математики МБОУ СОШ С. Сокол, Долинский район, Сахалинская область.
Урок геометрии в 8 классе
Тема урока: Касательная к окружности.
Цели:
Обучающие: повторить и систематизировать полученные знания по данной теме: повторить понятия касательной, точки касания, отрезков касательных, проведенных из одной точки; формировать умения использовать свойства касательной и ее признак при решении задач; повышать вычислительную культуру учащихся; выявить и ликвидировать ошибки и затруднения по изученной теме.
Развивающие: развивать умение пользоваться свойствами касательной и отрезками касательных в процессе решения задач; грамотную речь; развитие памяти; навыков самостоятельной работы и самооценки; умение анализировать, проводить обобщение.
Воспитывающие: воспитание умения работать в паре; взаимной ответственности за результаты учебного труда; прививать чувство самокритичности в оценке своей работы наряду с чувством уверенности в правильности ее выполнения; воспитание познавательного интереса к предмету.
Тип урока: урок обобщения и систематизации полученных знаний и выполнения практических самостоятельных работ.
Оборудование: учебник « Геометрия. 7 – 9 классы. Атанасян Л.С., Бутузов В.Ф. и др.»; задания для самостоятельной работы; презентация MS Power Point ,ПК, экран, проектор.
Ход урока:
Организационный момент.
На прошлом уроке мы с вами, начали изучать тему взаимное расположение прямой и окружности. Выяснили, что прямая и окружность в зависимости от их взаимного расположения могут иметь 2, 1 общую точку или не иметь общих точек вообще. Если расстояние от прямой до центра окружности, больше радиуса окружности, то прямая и окружность не имеют общих точек. Если расстояние от прямой до центра окружности меньше радиуса, то прямая пересекает эту окружность в двух точках. Прямую в этом случае можно назвать секущей. Если же расстояние от прямой до окружности равно радиусу этой окружности, то прямая и окружность имеют 1 общую точку. Прямая в этом случае называется касательной. Например, рассмотрим № 345 устно. Выяснить взаимное расположение прямой и окружности. О касательной на прошлом уроке мы остановились более подробно. Изучили ее свойство и признак, также изучили свойство отрезков касательных, доказали каждое утверждение.
Сегодня нам необходимо повторить, все то, что изучили про касательную и порешать задачи. Значит, цель нашего урока, какая? Повторить знания, полученные при изучении темы «Касательная к окружности», получить навыки решения задач, используя полученные знания.
Итак, начнем нашу работу.
Актуализация опорных знаний.
Прежде чем начать решать задачи, нам необходима теория. Как вы подготовлены по теории? Знаете ли вы её? Составьте из слов необходимые свойства. Напоминаю, говорим о касательных.
Итак, какая же теория нам необходима? Работа в группах
Нужно составить из слов необходимые свойства
- теорема о свойстве касательной.
- теорема о свойстве отрезков касательных к окружности, проведенных из одной точки.
- теорема, признак касательной. Итак, прочитайте, что у вас получилось
Свойство касательной. Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
Свойства отрезков касательных. Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
Признак касательной. Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна к этому радиусу, то она является касательной.
Решение задач. Решение задач на готовых чертежах. Устно. (дети должны говорить)
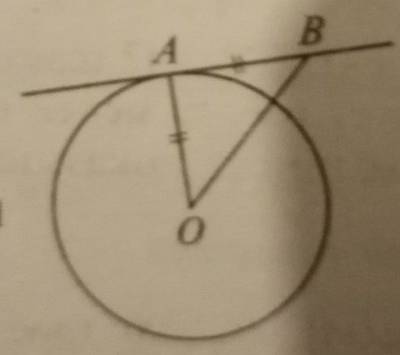
Дано: AB – касательная; AB=12, OB=13. Найти: R
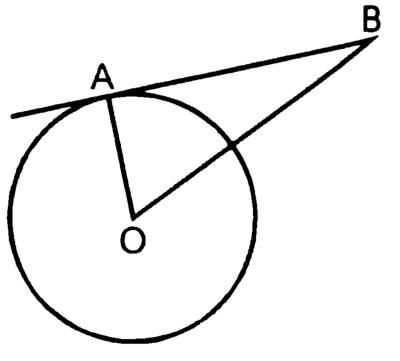
ответы: ; 1) R = 5
Дано: AB, BC – касательные, ВОС =130°.Найти: ВАС
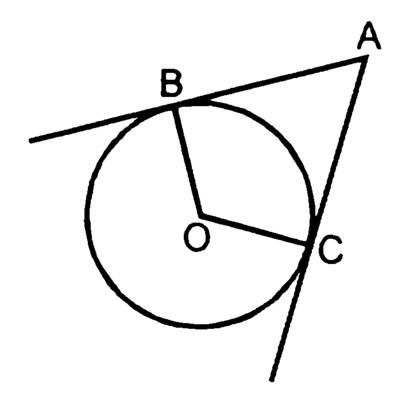
угол ВАС = 500 .
Решение задач. Совместно
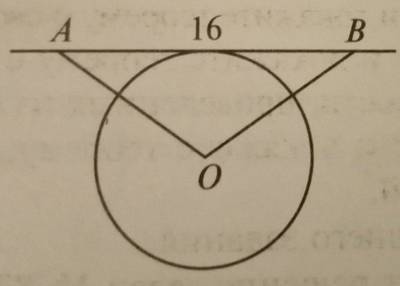
Прямые АВ и АС касаются окружности с центром О в точках В и С. Найдите ВС, если0, АВ=5 см. ( )
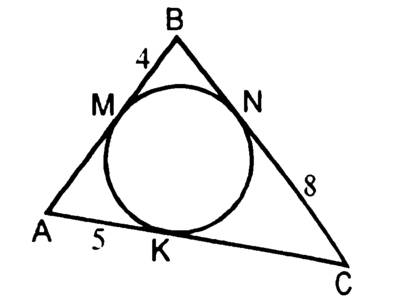
Дано: M, N, K – точки касания. Найти: Р треугольника АВС. (МВ = ВN=4, NC=KC=8, АМ= АК=5 по свойству отрезков касательных проведенных из одной точки. Значит АВ=9, ВС = 12, АС=13. Р = 9+ 12 + 13 = 34)
Физкультминутка.
- Мы устали чуточку, отдохнем минуточку.
- Кто согласен с тем, что «Прямая является касательной по отношению к окружности, если она имеет одну общую точку с ней». – встаньте.
- Нарисуйте глазками окружность, а теперь головой, туловищем.
-Улыбнитесь соседу справа, улыбнитесь соседу слева.
- Молодцы, тихонечко садитесь.
Самостоятельная работа.
Развитие навыков самостоятельной работы и самооценки.
Ребята, вам предлагается выполнить самостоятельную работу (в двух вариантах). К задачам необходимо записать полное решение. И в первой и второй задаче обязателен чертеж (10-12 минут).
Самооценка.
Проверьте, пожалуйста, свои ответы. Оцените свою работу. Если у вас решены правильно обе задачи, то 5, одна 4, если не одной то вам необходимо повторить изученный материал и на следующем уроке, вы еще будете решать задачи.
Домашнее задание.
Повторить п.42; № 351, подг. сообщ на тему касательная к окружности в повседневной жизни
Подведение итогов урока.
- Ребята, у кого были затруднения при выполнении заданий?
- Удалось ли их преодолеть?
- Как вы считаете, что необходимо повторить, или выучить, чтобы не возникало таких трудностей?
Ответы
Вариант1
1)ОЕ = 10 см
2) АО =10 см
Вариант 2
1) NO = 10 см
2) ОВ = √10 см
Самостоятельная работа
Вариант 1
1. Прямая КЕ касается окружности с центром в точке О, К – точка касания. Найдите ОЕ, если КЕ =8 см, а радиус окружности равен 6см.
2. АВ – касательная, R=6, АО=ОВ. Найти АО.
Вариант 2
1.Найдите NО. Если МN касается окружности с центром в точке О, М точка касания, радиус окружности равен 5 см, 0 .
2. АВ– касательная, R=√5, Найти ОВ.