Конспект урока по алгебре на тему: «Графическое решение показательных уравнений» (11класс)

20.01.25 Алгебра и начала анализа 11 класс

Конспект урока по теме: «Графические методы решения показательных уравнений

Цели урока:

Обучающая: - закрепить знания по теме «Показательная функция -отработать навыки решения уравнений графическим способом, -закрепить умения строить графики функций.

Развивающая: -способствовать развитию познавательной активности, логического мышления, умения правильно читать условие задачи: -развивать навыки самостоятельной работы, работы в группе, самоконтроля;

Воспитательная: -способствовать воспитанию активности, ответственного отношения к работе, самостоятельности.

Тип урока: систематизации, обобщения знаний.

Ход урока.

1. Орг.момент. Приветствие. Настрой на работу.

2. Проверка домашнего задания.

№ 446. Найти область определения функций:

а) у = -2^х; б) у = (1/3)^х; в) у = -(1/4)^х; г) у = 5^х – 2;

На доске схематически нарисовать графики функций, записать ответы.

Вопросы отвечающему: 1) Какая функция называется показательной?

2) Что служит областью определения показательной функции?

3) Когда показательная функция возрастает (убывает)?

1. Повторение, подготовка к ГИА (базовый уровень).

1) Установить соответствие между величинами и их значениями: к каждому элементу первого столбца подобрать соответствующий элемент из второго столбца.

ВЕЛИЧИНЫ ЗНАЧЕНИЯ

А) Рост жирафа 1) 6371 км

Б) Толщина лезвия бритвы 2) 500 см

В) Радиус Земли 3) 0, 08 мм

Г) Ширина футбольного поля 4) 68 км

2) На рисунке изображена зависимость температуры воздуха от высоты над уровнем моря. По горизонтали указана высота в метрах, по вертикали – значение температуры в градусах Цельсия. Определите по графику, на сколько градусов Цельсия воздух на высоте 250 м теплее, чем на высоте 650 м.

4.Сегодня вспоминаем графический способ решения уравнений. Вспомните.

Что называют уравнением?

Что значит решить уравнение?

Что называют корнем уравнения?

Что нужно сделать для того, чтобы решить уравнение графически?

Теоретический материал для самостоятельного изучения

1. Рассмотрим показательные уравнения.

Показательным называется уравнение, в котором переменная входит только в показатели степеней, при заданном основании.

Уравнения вида 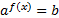 ,   называются простейшими показательными уравнениями.

В самом простом случае уравнение принимает вид:  .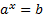

Так как множество значений показательной функции 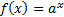  - множество положительных чисел, то при  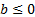 уравнение решений не имеет.

Теперь рассмотрим случай b0.

Вспомним, что показательная функция при a1 монотонно возрастает и принимает все положительные значения, каждое ровно один раз. В случае 0

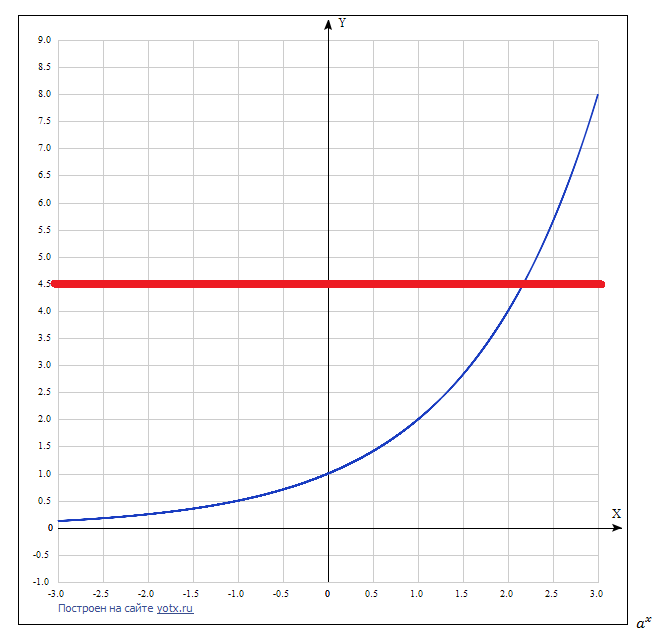
Рисунок 1 – иллюстрация решения простейшего показательного уравнения 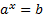 , a1.

Рисунок 2 – иллюстрация решения простейшего показательного уравнения 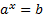 , 0.

Для того чтобы решить простейшее показательное уравнение 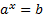 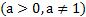  , нужно число b представить в виде степени числа a.

Рассмотрим пример:  .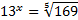

Представим 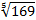  в виде степени числа 13:  .

Теперь перепишем данное уравнение в виде: 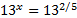 , поэтому x=2/5.

Ответ: x=2/5.

2. Теперь перейдем к решению более сложных показательных уравнений.

2.1. Рассмотрим уравнение вида:

.

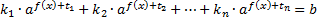То есть мы видим, что левая часть этого уравнения представляет собой сумму, слагаемые которого отличаются коэффициентами 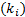  и показатели степеней с одинаковыми основаниям отличаются слагаемыми  .

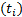Для решения таких уравнений левую часть преобразуют следующим образом: выносят за скобку степень 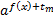  (часто, чтобы избежать дробных коэффициентов, выносят степень с наименьшим показателем):

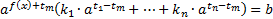
Мы видим, что выражение в скобках представляет собой число.

Поэтому выразим   и решим простейшее показательное уравнение.

Рассмотрим пример:

.

Решение:

Преобразуем левую часть и вынесем за скобку  :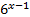

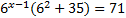
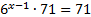
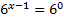
x-1=0

x=1

Ответ: x=1.

2.2. Рассмотрим еще одно уравнение, которое решается с помощью вынесения за скобку общего множителя.

.

Решение:

Преобразуем уравнение: перенесем степени с одинаковыми основаниями в одну часть:

,

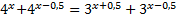Вынесем за скобку множители с одинаковыми показателями:

,  .

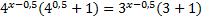Теперь преобразуем полученное уравнение к виду: 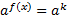 . Для этого разделим обе части уравнения на  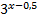 и на 3:

.

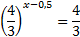x-0,5=1

x=1,5.

Ответ: x=1,5.

2.3. Еще один вид показательных уравнений – уравнения, сводящиеся к квадратным:

.

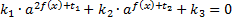В этом случае вводят новую переменную: 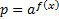 . Получим вспомогательное уравнение:  .

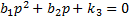После решения этого уравнения получим простейшие показательные уравнения.

Рассмотрим пример:

.

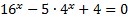Решение:

Введем новую переменную:  .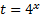

Запишем вспомогательное уравнение:  .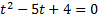

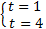 . Вернемся к переменной х:

 ,   .

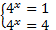Ответ: 

2.4. Еще один вид уравнений, который сведется к решению квадратного или уравнения третей степени, это однородное уравнение.

Однородным показательным уравнением называется уравнение вида:

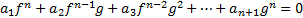
Здесь f и g функции вида: 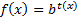 ,  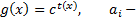 коэффициенты.

Однородные показательные уравнения решаются делением на 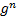  или на  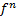 и последующей заменой:  .

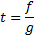Рассмотрим пример:

.

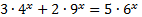Решение:

Заметим, что 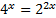 ,  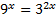,  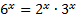. То есть уравнение можно записать в виде:

.

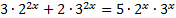Разделим уравнение на 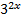 , получим уравнение:  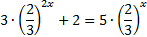. Теперь введем новую переменную:  и получим вспомогательное уравнение:

, решим его:

 .

 ,  .

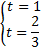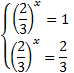Ответ:  .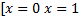

Примеры и разбор решения заданий тренировочного модуля

Пример 1.

Решите уравнение: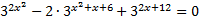 

Решение: Запишем уравнение в виде:

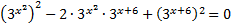
Таким образом, уравнение является однородным относительно функций:   и  .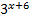

Разделим уравнение на 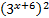  и получим:

.

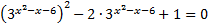Введем новую переменную:  .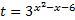

Вспомогательное уравнение:

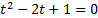
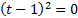
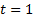
Вернемся к исходной переменной:

 .

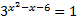
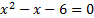
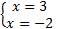Ответ:   .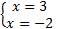

Пример 2.

Решите систему: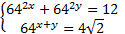 

Решение: Введем новые переменные:  .

Рассмотрим вспомогательную систему:

.

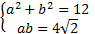Возведем второе уравнение в квадрат:

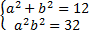. Решим полученную систему относительно  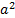 и   .

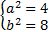 или  .

Так как 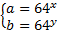 , то есть положительные, то

 или  .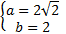

Вернемся к исходным переменным.

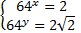 или  .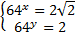

Отсюда:

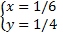 или  .

Ответ: (1/6; 1/4); (1/4; 1/6)

Работа у доски. Остальные в тетрадях.№ 458.

а) 3^1-х = 2х – 1. Решаем на доске. Преобразуем левую часть уравнения. Чтобы там была формула показательной функции. Как это сделать? Когда показатели степеней вычитаем? Что нужно сделать, чтобы избавиться от 3 в числителе? Приходим к уравнению: (1/3)^х =2/3х – 1/3. Обратить внимание, что ответом является только абсцисса точки пересечения графиков. Почему?

б) 4^х + 1 = 6 – х. Что нужно сделать, чтобы в левой части была формула показательной функции? Работают самостоятельно.

в) 2^х – 2 = 1 – х, г) 3^-х = -3/х – выполняют самостоятельно.

1. Задание для сильных учащихся № 455(а,б). Найти минимальное и максимальное значения функций.

а) у = (1/2)^{sin x}; б) у = 5 + 3^{|cos x|}.

1. № 454(б,г) Построить график и найти область значений функции.

б) у = |2^x – 2|; г) у = 4^|x|. Какие преобразования графиков функций нужно использовать при построении графиков?

1. Подведём итог урока. Что повторили или узнали на уроке? Что вызвало затруднения? Над чем ещё предстоит поработать?

1. Задание на дом: п. 35, № 457.

Дополнительное задание:

задача. Вкладчик положил в банк 10 000 рублей на срочный вклад на 5 лет под 9,8% годовых. Какую сумму получит вкладчик по истечении срока вклада?
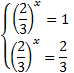