Конус. Презентация учеников.

Геометрия 11 класс

Конус

Выполнили ученики 11 «Б»класса

Раджабов Керим

Пекарев Игорь

Рассмотрим окружность L с центром О и прямую ОР, перпендикулярную к плоскости α этой окружности.

Через точку Р и каждую точку окружности проведем прямую. Поверхность, образованная этими прямыми, называется  конической поверхностью , а сами прямые —  образующими конической поверхности .

Точка Р называется  вершиной , а прямая ОР —  осью конической поверхности .

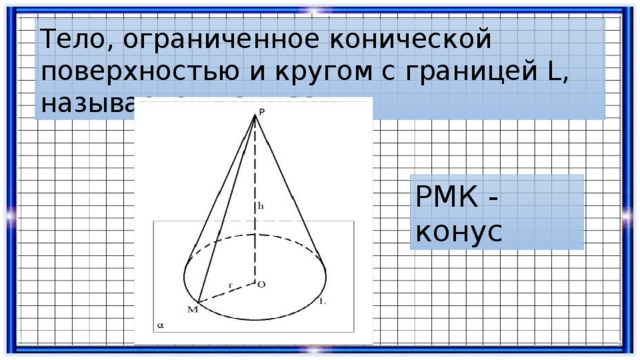
Тело, ограниченное конической поверхностью и кругом с границей L, называется  конусом.

РМК - конус

Круг называется  основанием конуса , вершина конической поверхности —  вершиной конуса , отрезки образующих, заключенные между вершиной и основанием —  образующими конуса , а образованная ими часть конической поверхности —  боковой поверхностью конуса .

Ось конической поверхности называется  осью конуса , а ее отрезок, заключенный между вершиной и основанием —  высотой конуса .

Все образующие конуса равны друг другу.

Р – вершина конуса

РМ – образующая конуса

РО – высота конуса (ось)

Круг L – основание конуса

МО – радиус основания

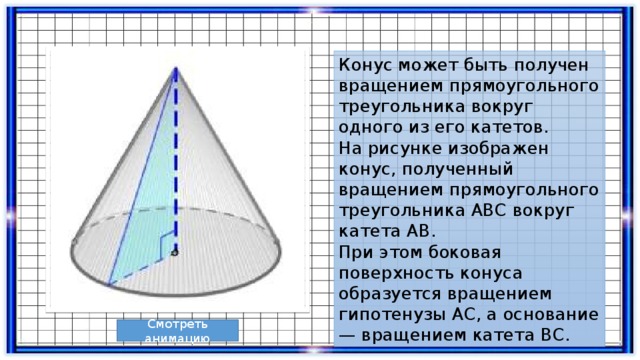
Конус может быть получен вращением прямоугольного треугольника вокруг одного из его катетов.

На рисунке изображен конус, полученный вращением прямоугольного треугольника АВС вокруг катета АВ.

При этом боковая поверхность конуса образуется вращением гипотенузы АС, а основание — вращением катета ВС.

Смотреть анимацию

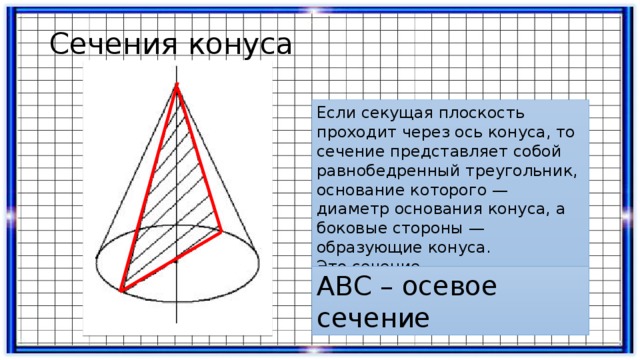
Сечения конуса

Если секущая плоскость проходит через ось конуса, то сечение представляет собой равнобедренный треугольник, основание которого — диаметр основания конуса, а боковые стороны — образующие конуса.

Это сечение называется  осевым.

АВС – осевое сечение

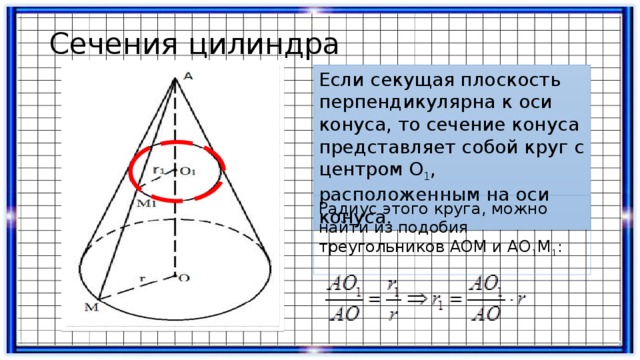
Сечения цилиндра

Если секущая плоскость перпендикулярна к оси конуса, то сечение конуса представляет собой круг с центром О 1 , расположенным на оси конуса.

Радиус этого круга, можно найти из подобия треугольников AOM и AO 1 M 1 :

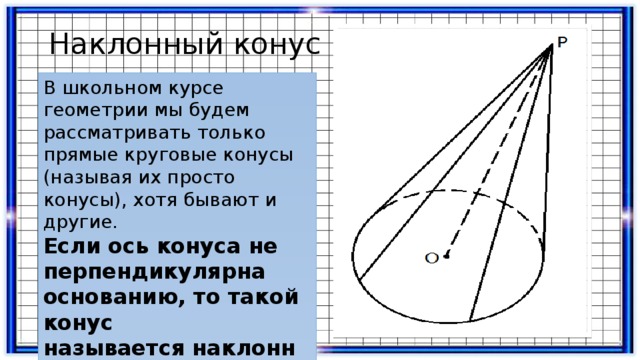
Наклонный конус

В школьном курсе геометрии мы будем рассматривать только прямые круговые конусы (называя их просто конусы), хотя бывают и другие.

Если ось конуса не перпендикулярна основанию, то такой конус называется наклонным.

Конус в природе

Египетская пустыня

Конус в природе

Конус в архитектуре

Библиотека Делфтского технического университета, Южная Голландия, Нидерланды. 

Конус в архитектуре

Midrand Water Tower, South Africa На 6 000 000 литров — крупнейшая водонапорная башня в Южном полушарии. В основе диаметр конуса 4 метра, на высоте ствол — 10 метров.

Конус в архитектуре

«Вигвам» – название американской сети мотелей с уникальными номерами в форме типи. Они были построены в 1930-х годах.

Конус в архитектуре

Гигантский конус Кафедрального собора Пресвятой Девы Марии в Маринге архитектора Жозе Аугусто Беллуччи. 

Конус в жизни

Солнечная электростанция из конусов

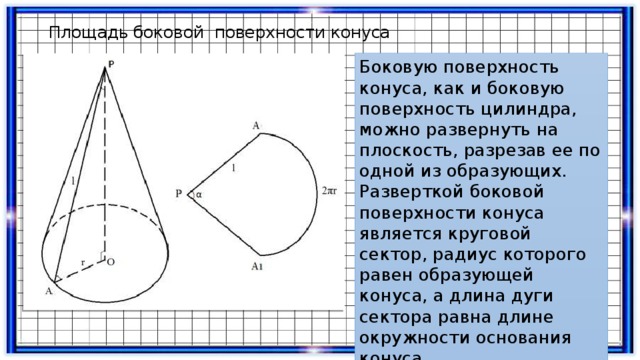
Площадь боковой  поверхности конуса

Боковую поверхность конуса, как и боковую поверхность цилиндра, можно развернуть на плоскость, разрезав ее по одной из образующих.

Разверткой боковой поверхности конуса является круговой сектор, радиус которого равен образующей конуса, а длина дуги сектора равна длине окружности основания конуса.

Площадь боковой  поверхности конуса

За площадь боковой поверхности конуса принимается площадь ее развертки.

Площадь боковой  поверхности конуса

S бок = Пrl

r- радиус основания

l - образующая

Площадь полной поверхности конуса

Площадью полной поверхности конуса называется сумма площадей боковой поверхности и основания.

Так как площадь основания равна πr 2 , то для вычисления площади  полной поверхности конуса получаем формулу:

Спасибо за внимание