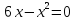Старт осенних олимпиад для учителей, учеников и дошкольников! Специальные наградные, результаты сразу, комфортное участие.

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ

Благодаря готовым учебным материалам для работы в классе и дистанционно

Выбрать материалы

Скидки до 50 % на комплекты
только до

Готовые ключевые этапы урока всегда будут у вас под рукой

Организационный момент

Проверка знаний

Объяснение материала

Закрепление изученного

Итоги урока

Был в сети 30.09.2024 09:37

Жумабай Ержан Сабитбекулы

учитель математики

31 год

227

153 750

Подписчики

Подписки

Обо мне Блог Файлы Тесты Галерея Активность Награды

Квадратные уравнения

Категория: Математика

11.06.2019 09:48

Организационный момент. Целеполагание.

Учитель приветствует учащихся, проверяет готовность учащихся к уроку. Учитель объявляет тему урока и цели обучения. Совместно с учащимися формулируются цели урока. Далее учитель озвучивает критерии оценивания, определяет «зону ближайшего развития» учащихся, ожидания к концу урока.

Повторение.

Для обеспечения глубокого усвоения учащимися новой темы учитель задает следующие вопросы для повторения:

Неравенство какого вида называется квадратным?

Назовите методы решения квадратных неравенств?

Объясните суть метода интервалов?

Как решить квадратное неравенство с помощью графика квадратичной функции?

Затем учитель предлагает учащимся выполнить несколько заданий на решение квадратных неравенств, применив различные методы их решения.

После завершения этапа повторения учащиеся совместно с учителем делают выводы.

Введение алгоритма решения систем неравенств.

Учитель объясняет учащимся, что решить систему неравенств – это значит найти значение переменной, при котором верно каждое из неравенств системы.

Затем учитель формулирует алгоритм решения систем неравенств:

1) решаем каждое неравенство системы отдельно;

2) изображаем полученные решения на числовой прямой и находим пересечение этих решений.

Эта общая часть и является решением данной системы неравенств.

После учитель задает учащимся вопрос:

Каким будет решение системы неравенств, если одно из его неравенств имеет решение

а) ∅;

б) R?

Учащиеся отвечают на вопрос, учитель дополняет их ответы и подводит итоги.

Мотивационный момент.

С целью поддержания интереса к изучаемой теме учитель объясняет учащимся значение термина система и указывает, что в повседневной практике слово «система» может употребляться в различных значениях:

теория, например, философская система Платона;

классификация, например, Периодическая система химических элементов Д. И. Менделеева;

метод практической деятельности, например, система Станиславского;

способ организации мыслительной деятельности, например, система счисления;

совокупность объектов природы, например, Солнечная система;

некоторое свойство общества, например, политическая система, экономическая система и т.д.

Разбор примера решения системы неравенств.

Учитель совместно с учащимися решает систему неравенств, обращая внимание на все этапы решения.

Учащиеся задают вопросы, ведется обсуждение со всем классом.

Решение задач на составление систем неравенств.

Учитель предлагает учащимся выполнить задание на нахождение области определения функции, а также решить текстовую задачу через составление и решение систем неравенств.

После завершения работы над заданиями учащиеся совместно с учителем подводят итоги.

Работа в парах.

Учащиеся в парах выполняют задания на составление и решение системы неравенств. Учитель оказывает помощь учащимся при затруднении. Типичные ошибки учащихся разбираются совместно со всем классом. Учитель при необходимости может организовать работу у доски при этом делая акцент на оформление решения.

Задание. Решите задачу, составив систему неравенств:

На рисунке показана схема цветочной клумбы.

а) Найдите все возможные размеры клумбы, если известно, что ее площадь не более 16 м2, а ее стороны выражены целыми числами.

б) Сколько метров бордюра потребуется для того, чтобы огородить такую клумбу?

Учитель оценивает работу учащихся согласно установленным критериям, а также наблюдает за вкладом каждого ученика в ходе парной работы.

Критерии оценивания:

Учащийся

составляет квадратное неравенство по условию задачи;

составляет линейное неравенство по условию задачи;

составляет систему двух неравенств;

верно решает систему неравенств;

записывает ответ в соответствии с условием задачи.

Индивидуальная работа.

Учащимся предлагаются задания для индивидуальной работы. Учитель наблюдает за выполнением заданий учащимися, задает им вопросы, направляя на верное решение, оказывает консультативную помощь, оценивает работы учащихся по критериям, предоставляет обратную связь учащимся.

Критерии оценивания к заданию №1:

Учащийся

верно решает квадратное неравенство;

верно решает линейное неравенство;

решает систему неравенств;

правильно записывает ответ.

Критерии оценивания к заданию №2:

Учащийся

верно составляет систему неравенств;

решает систему неравенств;

правильно записывает ответ.

Просмотр содержимого документа
«Квадратные уравнения»

Раздел долгосрочного плана:

8.2A: Квадратные уравнения

Школа:

Дата

Имя учителя:

Класс: 8

Количество присутствующих:

Тема урока

Квадратное уравнение

Определение квадратного уравнения

Урок №1 серии из 3 уроков

Тип урока

Изучение новой темы

Цели обучения, которые достигаются на данном уроке (ссылка на учебную программу)

8.2.2.1

знать определение квадратного уравнения

Цели урока

Учащиеся знают определение квадратного уравнения.

Критерии оценивания

Навыки

Критерий оценивания

Знание и понимание

Знает определение квадратного уравнения

Различает квадратные уравнения

Приводит квадратные уравнения к виду

Применение знаний

Составляет квадратное уравнение по его коэффициентам

Языковые цели

Учащиеся формулируют определение квадратного уравнения.

Предметная лексика и терминология:

Квадратное уравнение

коэффициент

показатель степени

Серия полезных фраз для диалога/письма

Квадратное уравнение – это уравнение, в котором …

самым высоким показателем переменной является квадрат

Уравнение содержит переменную в третьей степени, поэтому не является квадратным

Привитие ценностей

Умение учиться, принимать самостоятельные решения.

Привитие ценностей осуществляется посредством работ, запланированных на данном уроке.

Межпредметные связи

Квадратные уравнения являются математической моделью многих процессов реальной жизни.

Навыки использования ИКТ

Использование интерактивной доски в качестве демонстрационного средства и средства записи.

Первоначальные знания

Учащиеся знают понятие уравнения, умеют решать линейные уравнения.

Ход урока

Этапы урока

Запланированная деятельность на уроке

Ресурсы

Начало урока

2 мин

5 мин

Организационный момент

Создание положительного эмоционального настроя. Сообщение темы и цели урока.

Актуализация знаний

Математический диктант.

Учитель дважды читает задание, учащиеся записывают ответы на листочках. После окончания диктанта учащиеся меняются листочками и проверяют работы друг друга. Обсуждая ответы с учителем.

Представьте в виде многочлена:

(9х – 1)(9x + 1) =
(2x + 7)(7 – 2х)=
(x + 3)(3x-5)=

Презентация

Слайд 1

Середина урока

10 мин

12 мин

13 мин

Изучение нового материала

При изучении нового материала используется диалоговое обучение.

- Приведите примеры уравнений, содержащих переменную в первой степени.

- Как называются такие уравнения? Линейные уравнения.
- Вспомните общий вид линейного уравнения.

(kx+ b = 0, k ≠ 0)

- Какова степень следующих уравнений:

5х + 8 = 23, 2y – 7 = 5y +14?

- Теперь рассмотрим уравнения, содержащие переменную во второй степени. Приведите примеры таких уравнений.

- Такие уравнения называют квадратными уравнениями.

Уравнения вида ax²+ bx+ c = 0, где a, b, c – некоторые числа, причем а ≠ 0, х – переменная, называется квадратным уравнением.

Число а называют первым или старшим коэффициентом, b – вторым коэффициентом, c – свободным членом.
- В квадратном уравнении а ≠ 0. Почему?

- Могут ли коэффициенты b или c равняться нулю?

- Приведите примеры таких уравнений.

- Назовите коэффициенты в следующих уравнениях:

х² + 400 = 0 ; 8х² -56х = 0 ; -х² = 0.

Закрепление материала

№1. Среди приведенных в таблице уравнений выберите квадратные и запишите их коэффициенты.

Уравнение	Уравнение квадратное или нет?	Коэффициенты квадратного уравнения
Уравнение	Уравнение квадратное или нет?	a	b	c
-25х + 1 = 0


2,5х + 1,5х+3 = 0



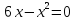
3х = 0

Проверка ответов по слайду 4:

№2. Приведите уравнения к виду квадратного уравнения и запишите его коэффициенты.

а) 3х(х – 2) + (х – 1)(x + 1) = - 2

b) (2x - 1)² – (3x + 2)(3x – 2) = 0

c) (x – 4)(x + 4) + (2x + 1)² = 4x

d) (5x – 1)² – (5x + 1)² = (4x + 1)²+(4x -1)².

Индивидуальная работа по карточкам

Учащиеся самостоятельно выполняют задания по карточкам, затем в группах сравнивают результаты, обсуждают решения, оценивают работы, используя дескрипторы.

Карточка 1

1. Приведите уравнения к виду ах²+ bх + с = 0:

(x – 3)(3x + 2) = (5х – 4)(3х – 2).

2. Запишите квадратное уравнение, если известны его коэффициенты:

а) a = 7, b = - 2, c = 1. b) a = -2, b = 5, c = 3

c) a = -1, b = - 3, c = 7 d) a = 5, b = 4, c = -7

e) a = -5, b = 0, c = -1 f) a = 3, b = 4, c = 0.

3. Среди данных уравнений выберите квадратные и запишите их коэффициенты:

а) 2х² +3х – 1 = 0 b) 3x + 2 = 2x - 1

c) –x - 3xy = 2xy +1. d) x² - 8x – 9 = 0

Карточка 2

1. Приведите уравнения к виду ах²+ bх + с = 0:

(2x + 7)(7 – 2х) = 49 + х(х + 2).

2. Запишите квадратное уравнение, если известны его коэффициенты:

а) a = 37, b = - 2, c = 14. b) a = -12, b = 7, c = 31

c) a = -41, b = - 23, c = 17 d) a = 7, b = 14, c = -2

e) a = -3, b = 0, c = -7 f) a = 15, b = 6, c = 0.

3. Среди данных уравнений выберите квадратные и запишите их коэффициенты:

а) 3х² +2х – 3 = 0 b) 4x + 7 = 3x - 4

c) –5x - 2xy = 4xy +7. d) x² - 5x – 6 = 0

Карточка 3

1. Приведите уравнения к виду ах²+ bх + с = 0:

(x + 7)(x² – 7х + 49) = х(х + 8)(х – 7).

2. Запишите квадратное уравнение, если известны его коэффициенты:

а) a = 21, b = - 24, c = 4. b) a = -15, b = 7, c = 21

c) a = -11, b = - 31, c = 2 d) a = 17, b = 10, c = -3

e) a = -5, b = 0, c = -2 f) a = 4, b = 5, c = 0.

3. Среди данных уравнений выберите квадратные и запишите их коэффициенты:

а) 5х² +7х – 2 = 0 b) 6x – 15 = 8x - 3

c) –x -9xy = 3xy + 5. d) x² - 9x – 10 = 0

Учитель проверит работы учащихся по следующим дескрипторам:

Критерий оценивания	Дескрипторы
Знает определение квадратного уравнения	Приводит уравнение к виду квадратного
	Составляет квадратные уравнения
	Отбирает среди уравнений квадратные Называет коэффициенты квадратного уравнения

Слайды 2-3

Приложение 1

Слайд 4

Слайды 5-6

Приложение 2

Слайд 7

Конец урока

3 мин

Рефлексия:

Внутренний и внешний круги.

Учащиеся переходя по кругу по порядку заканчивают предложения:

Сегодня я узнал ...

Мне было интересно ...

Мне было трудно ...

Я понял ...

Теперь я ...

Домашнее задание

Учащиеся обменяются в парах карточками и выполнят задания.

Слайд 8

Дополнительная информация

Дифференциация – как Вы планируете оказать больше поддержки? Какие задачи Вы планируете поставить перед более способными учащимися?

Оценивание – как Вы планируете проверить уровень усвоения материала учащихся?

Межпредметные связи
Здоровье и безопасность
Связи с ИКТ
Связи с ценностями (воспитательный элемент)

Дифференциация заключается в различии ожиданий от учащихся.

Учитель будет наблюдать за работой учащихся. В конце урока будет дано письменно задание для формативного оценивания.

На уроке будет проведена физминутка.

Кабинет проветрен к началу урока.

Рефлексия

Были ли реализованы цели урока/Ожидаемые результаты реалистичными? Чему сегодня научились учащиеся? Какова была атмосфера в классе? Сработала ли дифференциация? На все ли хватило времени? Какие изменения были внесены в план и почему?

Используйте данный раздел для рефлексии урока. Ответьте на вопросы о Вашем уроке из левой колонки.

Общая оценка

Какие два аспекта урока прошли хорошо (подумайте как о преподавании, так и об изучении)?

Какие две вещи могли бы улучшить урок (подумайте как о преподавании, так и об изучении)?

Что я узнал(а) за время урока о классе или отдельных учениках такого, что поможет мне подготовиться к следующему уроку?