Логическое мышление младших школьников

Содержание

1.Введение.

1.1 Логика как наука.

1.2 Необходимость развития логического мышления у детей младшего школьного возраста.

2. Развитие логического мышления младших школьников.

2.1 Особенности логического мышления младших школьников.

2.2 Развитие логического мышления младших школьников на уроках математики в условиях введения ФГОС.

2.3 Система упражнений по логическому мышлению.

2.4 Формы внеурочной работы.

3. Заключение.

4. Список использованной литературы.

Проблема проекта: Никто не будет спорить с тем, что каждый учитель должен развивать логическое мышление учащихся. Об этом говорится в методической литературе, в объяснительных записках к учебным программам. Однако, как это делать, учитель не всегда знает. Нередко это приводит к тому, что развитие логического мышления в значительной мере идет стихийно, поэтому большинство учащихся, даже старшеклассников, не овладевает начальными приёмами логического мышления (анализ, сравнение, синтез, абстрагирование и др.)

Цель проекта: теоретически разработать и проверить эффективность системы упражнений, способствующих развитию творческих способностей младших школьников в процессе обучения математике.

Задачи проекта:

1. Изучить психолого – педагогическую литературу по проблеме исследования.

2. Выявить уровень развития логического мышления.

3. Составить систему упражнений, способствующих развитию логического мышления на уроках и во внеурочное время.

Ожидаемый результат:

- развитие мыслительных операций: сравнение, анализ, синтез, классификация, абстракция и обобщение;

- знакомство учащихся с приемами решения нестандартных заданий;

- развитие интеллектуальных способностей;

- повышение интереса учащихся к изучению математики.

Введение

Термин «логика» происходит от греческого слова «логос», что означает «мыслить», «разум». Логика – есть наука о законах и формах правильного мышления. Она изучает формы рассуждений, отвлекаясь от конкретного содержания, устанавливает, что из чего следует, ищет ответ на вопрос: как мы рассуждаем? Основоположником логики как науки является древнегреческий философ и ученый Аристотель. Он впервые разработал теорию логического вывода.

Одна из важнейших задач современной школы - создание в системе обучения таких условий, которые бы способствовали развитию у ребенка логического мышления. Дорог каждый день жизни детей, начиная с самого рождения, а тем более нельзя упустить время в первые школьные годы. Усвоение знаний – большой и нелегкий труд. Он требует от учащихся максимальной отдачи и интеллектуальных сил, длительных и напряженных усилий, постоянной мобилизации воли и внимания. Учение требует особой мотивации, создание у учащихся побудительных сил и потребностей в приобретении знаний, то есть того, из чего складываются умения и желание учиться в школе, а затем самостоятельно овладевать знаниями. От нас, учителей, требуется определение условий, обеспечивающих высокую познавательную активность учащихся в процессе обучения. Важно не только разработать учебный материал, но и тщательно отобрать средства усвоения, обеспечив способ организации усвоения. Известно, что младший школьный возраст – благоприятный период для развития мыслительных операций: сравнение, анализ, синтез, классификация, абстракция и обобщение, то есть развития логического мышления

От того, насколько сформировано мышление у ребёнка, будет во многом зависеть успешность обучения вообще, и математике в частности. Ведущую роль в развитии логического мышления играет работа в начальной школе.

Возникает вопрос, а как же улучшить мыслительную деятельность учащихся, сделать их ум более гибким, научить мыслить, какие средства использовать.

Развитие логического мышления младших школьников

Мышление детей младшего школьного возраста значительно отличается от мышления дошкольников. Для мышления дошкольников характерно такое качество, как непроизвольность, малая управляемость и в постановке мыслительной задачи и в её решении, они чаще и легче задумываются над тем, что им интересно, что их увлекает. Младшие школьники, когда возникает необходимость регулярно выполнять задания в обязательном порядке, учатся управлять своим мышлением, думать тогда, когда это нужно, а не только тогда, когда интересно, когда нравится то, о чём надо думать.

Конечно, в 6-7 лет понятийное мышление еще не сформировалось, и все же задатки этого вида мышления уже есть.

Логическое мышление, по мнению А.А.Люблинской, обнаруживается, прежде всего, в протекании самого мыслительного процесса. В отличие от практического, логическое мышление осуществляется только словесным путём. Человек должен рассуждать, анализировать и устанавливать нужные связи мысленно, отбирать и применять к данной ему конкретной задаче известные ему подходящие правила, приёмы, действия. Он должен сравнивать и устанавливать искомые связи, группировать разное и различать сходное, и всё это выполняется лишь посредством умственных действий.

Огромное значение в учебной деятельности младшего школьника имеет операция сравнения. Ведь большая часть материала именно в младших классах построена на сравнении. Эта операция лежит в основе классификации явлений и их систематизации. Для овладения операций сравнения человек должен научиться видеть сходное в разном и разное в сходном.

Исследования показали также, что для логического мышления младших школьников характерна еще одна особенность – однолинейное сравнение, т.е. они, устанавливают либо только различие, не видя сходства (чаще всего), либо только сходное и общее, не устанавливая различного. К тому же выступает заметная разница между практическим установлением сходства и различия и умением доказывать, обосновать свое суждение, т.е. объяснить, что такое “сравнение” и что означает “сравнить”.

Если практически в начале года 38% учащихся I класса называли либо 1-2 признака сходства, либо столько же признаков различий, то только 3-9% из числа учащихся могли объяснить, что они делают, когда находят сходные или различительные признаки

Совершенствование логических умозаключений сохраняется и в других мыслительных процессах: в установлении причинно-следственных связей, в классификации и ответах на поставленные взрослыми вопросы, требующие планирования, догадки, поиска решения.

Таким образом, говоря об особенностях мышления младшего школьника и, опираясь на всё указанное выше, можно сделать следующие выводы:

1.Особенности логического мышления младших школьников проявляются и в самом протекании мыслительного процесса, и в каждой его отдельной операции (сравнении, классификации, обобщении, совершающихся в разных формах суждения и умозаключения).

2.Для мышления младших школьников характерно однолинейное сравнение (они устанавливают либо только различие, либо только сходное и общее).

3.Для мышления маленького ребенка характерен процесс, идущий путем “короткого замыкания”, минуя развёрнутый этап анализа.

4.Детям 7-10 лет доступны логические суждения, оперирования понятиями, переходы к обобщениям и выводам.

Для познания окружающего мира недостаточно лишь заметить связь между явлениями, необходимо установить, что эта связь является общим свойством вещей. На этой обобщённой основе человек решает конкретные познавательные задачи. Логическое мышление даёт ответ на такие вопросы, которые нельзя разрешить путём непосредственного, чувственного отражения. Благодаря развитию индивидуальных качеств мышления, человек правильно ориентируется в окружающем мире, используя ранее полученные обобщения в новой, конкретной обстановке.

Развивая своё логическое мышление, мы способствуем работе интеллекта, а интеллект – это гарантия личной свободы человека и самодостаточности его индивидуальной судьбы. Чем в большей мере человек использует свой интеллект в анализе и оценке происходящего, тем в меньшей мере он податлив к любым попыткам манипулирования им извне.

На сегодняшний день общеобразовательная школа выступает в качестве того общественного учреждения, которое самым непосредственным образом отвечает за качество человеческой истории.

Каждое поколение людей предъявляет свои требования к школе. Раньше первостепенной задачей считалось вооружение учащихся глубокими знаниями, умениями и навыками. Сегодня задачи общеобразовательной школы иные. Обучение в школе не столько вооружает знаниями, умениями, навыками. На первый план выходит формирование универсальных учебных действий, обеспечивающих школьникам умение учиться, способность в массе информации отобрать нужное, саморазвиваться и самосовершенствоваться.

Появились новые Федеральные образовательные стандарты общего образования второго поколения, в которых прописано, что главной целью образовательного процесса является формирование универсальных учебных действий, таких как: личностные, регулятивные, познавательные, коммуникативные. В соответствии стандартам второго поколения познавательные универсальные действия включают: общеучебные, логические, а также постановку и решение проблемы.

К логическим универсальным действиям относятся:

- анализ объектов с целью выделения признаков (существенных, несущественных);

- синтез - составление целого из частей, в том числе самостоятельное достраивание с восполнением недостающих компонентов;

- выбор оснований и критериев для сравнения, сериации, классификации объектов;

- подведение под понятие, выведение следствий;

- установление причинно-следственных связей;

- построение логической цепи рассуждений;

- доказательство;

- выдвижение гипотез и их обоснование.

Из вышесказанного следует, что уже в начальной школе дети должны овладеть элементами логических действий (сравнения, классификации, обобщения и др.). Поэтому одной из важнейших задач, стоящих перед учителем начальных классов, является развитие всех качеств и видов мышления, которые позволили бы детям строить умозаключения, делать выводы, обосновывая свои суждения, и, в конечном итоге, самостоятельно приобретать знания и решать возникающие проблемы. Никто не будет спорить с тем, что каждый учитель должен развивать логическое мышление учащихся.

Опыт показывает, что именно на уроках математики может происходить целенаправленное, систематическое формирование логических понятий и действий, т. к. именно в ней, в силу её специфических особенностей, содержатся большие потенциальные возможности для развития логического мышления младших школьников.

В связи с введением ФГОС одним из требований к выпускникам начальной школы является готовность школьника «самостоятельно действовать». Умение решать задачи повышенной сложности может способствовать развитию качеств, удовлетворяющих требованию стандарта. Одним из показателей умения действовать творчески является успешное выступление на олимпиадах, где ученик должен проявить сообразительность в нестандартной ситуации. Опыт показывает, что можно способствовать развитию мыслительной деятельности на уроках и во внеурочной деятельности. Включение задач повышенной сложности в учебный материал уроков математики способствует усилению развивающей функции обучения. В то время как в факультативном курсе по внеурочной деятельности создаются условия для развития у детей творческого потенциала, познавательной активности, мыслительной деятельности. Поэтому в своей работе практикую проведение занятий курса «Математическая шкатулка», где основной целью является обучение детей решению задач повышенной трудности. При этом важно, чтобы эти занятия не превратились в хаотичное решение заданий разных типов, а носили упорядоченный характер, где существует строгая логика построения учебного содержания. Важно, чтобы задания могли быт систематизированы по общему способу их решения и представлены в виде модели (знаковой, геометрической, диаграммы, алгоритма действий и т. д.).

Известно, что большие трудности для учащихся представляет решение текстовых задач. Известно и то, какой этап решения особенно труден. Это самый первый этап – анализ текста задачи. В тексте важно всё: и действующие лица, и их действия, и числовые характеристики. При работе с математической моделью задачи (числовым выражением или уравнением) часть этих деталей опускается. Но мы именно и учим умению абстрагироваться от некоторых свойств и использовать другие.

Существует различные методы решения задач:

- алгебраический;

- арифметический;

- графический;

- практический;

- метод предположения;

- метод перебора.

Они могут применяться при решении нестандартных задач. К нестандартным задачам относятся: «отгадывание чисел», «логические концовки», «задачи-парадоксы с неожиданными ответами», «занимательные задачи на расстановку чисел» и др.

Например: - Задумайте число, меньшее 10, но большее 0. Умножьте его на 10, прибавьте 6. Зачеркните первую цифру (число десятков зачеркнули). Получилось 6!

- Дом короче сарая, значит сарай …..

- Саша вышел из дома раньше, чем Серёжа, значит Серёжа …..

- Требуется уменьшить число 9 на 3. Как получить ответ, не используя никаких знаков? (Достаточно повернуть цифру 9, и ответ готов: получилась цифра 6!)

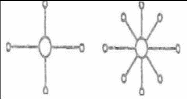
- Расставить числа так, чтобы сумма чисел вдоль каждого луча была равна одному и тому же числу – 10.

Мало уделяется внимания решению задач разными способами в основном из-за нехватки времени. А ведь умение решать задачи разными способами свидетельствует о достаточно высоком математическом развитии. Например, детям предлагается решить задачу разными способами. При решении задачи определенным способом дети аргументируют выбор способа.

Задача. На первой грядке росло в 5 раз больше кустов клубники, чем на вто-

рой. Когда с первой грядки пересадили 22 куста на вторую грядку, то на грядках стало поровну. Сколько кустов клубники было на каждой грядке?

Решение.

Первый способ

1) 5+1=6 (частей) – всего;

2) 6:2=3 (части) – приходится на каждую грядку;

3) 5-3=2 (части) – пересадили с первой грядки на вторую;

4) 22:2=11 (к.) – столько кустов приходится на одну часть (было на второй

грядке);

5) 11х5=55 (к.) – столько кустов было на первой грядке.

Второй способ

1) 22+22=44 (к.) – на столько меньше кустов на второй грядке, чем на первой;

2) 44:4=11(к.) – столько кустов приходится на одну часть;

3) 11х5=55 (к.) – столько кустов было на первой грядке.

Третий способ

Построим графическую модель условия задачи.

На первой грядке 􀀀 􀀀 􀀀 􀀀 􀀀

􀀀 22 куста

1) 22:2=11(к.) – приходится на 1/5 всех кустов

2) 11х5=55 (к.) – столько кустов было на первой грядке.

В своей работе использую геометрический материал. Ребятам предлагается назвать предложенные геометрические фигуры, а потом разделить их на группы. Далее задания усложняются.

2.«Танграмм» - несложный «геометрический конструктор». Квадрат 8х8 см из картона, разрезают на 7 частей (2 больших квадрата, 1 средний, 2 маленьких треугольника, квадрат и параллелограмм). Используя все 7 частей, плотно присоединяя их одну к другой, можно составить очень много различных изображений по образцам, а потом и по собственному замыслу.

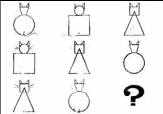
3.Даны 3 ряда изображений кошек, составленных из геометрических фигур. Недостающую в третьем ряду нужно найти на основе анализа, сравнения и обобщения. После выполнения таких заданий, ребята стараются составить свои аналогичные задания.

В работе с детьми я часто использую дидактические игры. На первый план при этом выдвигается умственная задача, для решения которой следует прибегнуть к сравнению, анализу и синтезу. В этих играх дети должны делать умозаключения и высказывать суждения. Это будет содействовать не только формированию логического мышления младших школьников, но и правильной, четкой, краткой речи. Логические игры являются именно такими, в которых путем цепочки несложных умозаключений можно предвидеть, предугадать необходимый результат, ответ. В этом их притягательная сила.

В играх ребенок проявляет инициативность и развивает находчивость, приучается к труду, к точности, аккуратности и настойчивости в преодолении препятствий. В играх развивается и укрепляется чувство товарищеской солидарности, честность, правдивость и другие качества, необходимые для коллективной работы и воспитания сознательной дисциплины.

Создание игровой атмосферы на уроке развивает познавательный интерес и активность учащихся, снимает усталость, позволяет удерживать внимание. В игре дети непроизвольно закрепляют, совершенствуют навыки вычисления. Младшие школьники очень любят соревноваться. Даже самые обычные упражнения, заданные в игровой форме, вызывают у них интерес.

«Узнай, какого цвета колпак на голове»

Из цветной бумаги изготовляют 3 колпака: красный, синий и зеленый. Учащиеся делятся на три команды. По одному ученику от каждой команды становятся спиной друг к другу. На них надевают колпаки. Затем играющие поворачиваются, и каждый, глядя на колпак другого, пытается догадаться, какой колпак на нем. После ответа они должны объяснить, как рассуждали. Ученик, который сумел объяснить свой ответ, получает 2 балла, а тот, кто просто отгадал, – 1 балл.

«Молодцы и хитрецы»

Каждый из присутствующих ребят мысленно называет себя «молодцом» или «хитрецом». При ответе на любой вопрос «молодцы» говорят только правду, а «хитрецы» всегда говорят неправду. Игра заключается в том, что один из учеников должен угадать, кто из ребят «молодец», кто «хитрец». Отгадывающий ученик выходит из класса, а все оставшиеся должны сказать друг другу, кто из них «молодец», а кто «хитрец». Затем отгадывающий входит в класс и говорит: «Оля, пусть Маня скажет тебе тихо, кто она: молодец или хитрец». (Маня что-то шепчет Оле.) Далее отгадывающий просит ответить на вопрос «Что сказала Маня?» По ответу Оли отгадывающий выясняет, кто Оля – молодец или хитрец.

Объяснение. По ответу Оли можно узнать безошибочно, кто она. Если Оля ответит: «Маня мне сказала, что она молодец», то и Оля назвала себя.

Игры с палочками развивают у детей умение самостоятельно осуществлять поиск способа решения. Они содержат задания на преобразование одних фигур в другие. Для их решения надо ставить фигуру по отдельным условиям или видоизменить ее: переложить, убрать указанное количество палочек с целью получения новой фигуры той же структуры, но с другим количеством квадратов или треугольников.

Более простыми являются задания на составление фигуры из палочек.

Составить из пяти палочек флажок; лопатку; два равных треугольника и

один четырехугольник.

Из шести палочек – домик, прямоугольник.

На втором этапе задания усложняются. Используются те решения, для которых нужно изменить положение палочек, убрав или переложив их. И цель здесь другая: учить детей рациональному способу решения задач (преобразованию). Необходимо проанализировать задачу, высказать предположение, прежде чем действовать практически.

В фигуре, состоящей из 6 квадратов, убрать 2 палочки, чтобы осталось 4

квадрата.

Третий этап обучения направлен на то, чтобы постепенно подводить детей к

решению задач в уме, направлен на развитие творческой мыслительной деятельности. Даются задания на более сложное преобразование путем перекладывания палочек.

В фигуре, состоящей из 4 квадратов, переложить 2 палочки, чтобы квадратов

стало 5.

Одна из форм внеурочной работы олимпиада. Она способствует воспитанию познавательного интереса, развитию творческих способностей, учит самостоятельно добывать знания, логически и нестандартно мыслить. 
Олимпиада–это соревнование и праздник. 
Олимпиада 4 класс 
I вариант 
1. Тройка лошадей бежала со скоростью 12 км/час. С какой скоростью 
бежала каждая лошадь? Обведи правильный ответ. 
12 км/час 24 км/час 4 км/час 36 км/час 
2. Нужно распилить 5 брёвен на 6 частей каждое. Сколько времени на это 
потребуется, если на один распил уходит 4 минуты? Обведи правильный 
ответ. 
20 мин 1 час 120 мин 1 час 40 мин 
3. Верна ли запись? Обведи правильный ответ. 
78249 х 342 х (22 — 11 х 2) 1 да нет 
4. Сколько груш и сколько яблок купила мама, если всего груш и яблок 25 
штук, при этом груши составляют пятую часть из них? Напиши ответы. 
Груш- ______________ яблок — ____________ 
5. У Оли и Тани было поровну вырезано цветов из бумаги. Оля сделала ещё 
один цветок, а потом ещё столько же, сколько получилось. А Таня — 
столько же, сколько было, а потом ещё один цветок. У кого из девочек 
стало бумажных цветов больше? Напиши имя девочки. ________________
6. Юра выставил свои 8 машинок в колонну. Какой длины получилась 
колонна, если длина каждой машинки 10см, а дистанция между 
машинками 2 см? Напиши ответ. _____________________________ 
7. Один ослик вёз 10 кг сахару, а другой ослик — 10 кг попкорна. У кого 
поклажа была тяжелее? Напиши ответ.________________________ 
8. В хозяйстве Попа было 13 работников. Каждый работник съедал в день 
каравай хлеба. Поп принял на работу Балду. 
Живет Балда в поповом доме, 
Спит себе на соломе, 
Ест за четверых, 
Работает за семерых. 
Поп прогнал лишних работников. Сколько караваев хлеба стал Поп 
экономить ежедневно? Напиши ответ.________________________________ 
9. В первом ряду ребята поставили 6 солдатиков на расстоянии 5 см один от 
другого, а во втором ряду солдатиков на расстоянии 3 см один от другого. 
Какой ряд длиннее? ___________________________________________ 
10. Играя, каждая из трёх подруг: Даша, Ира и Вика опустили в волшебный 
мешочек одну из своих игрушек: медвежонка, зайчика и слоника. 
Известно, что Даша не прятала зайчика. Вика не прятала зайчика и 
медвежонка. . Кто какую игрушку спрятал? Напиши ответы. 

Даша — _________________ 
Ира— __________________ 
Вика — __________________ 
Логические упражнения – представляют собой одно из средств, с помощью которого в опоре на жизненный опыт строятся правильные суждения, учатся сравнивать математические объекты, выполнять простейшие виды анализа и синтеза. 
II класс 
1. Которая из этих фигур лишня? Почему? 
2. Указать два признака различия в данных примерах: 
8 + 2 = 8 – 2
3. Если Оля сидит левее Тони, то, как сидит Тоня по отношению к Оле? 
4. Зина и Вера имеют фамилии Орлова в Скворцова. Какую фамилию имеет каждая из них, если известно, что Зина на два года моложе Орловой? 
Методический совет. Предлагая последнее задание, полезно на классной доске в один столбик записать оба имени и фамилии. 
5. Сколько разных четырехугольников на чертеже? 
6. Ответьте на вопрос: 
Все ученики II класса живут в деревне Ореховка. Толя — ученик II класса. Где живет Толя? Почему вы так думаете? 
7. Нина живет на пятом этаже, Катя — на восьмом. Петя и Коли - ниже Кати, но выше Нины. Петя живет ниже Коли. На каких этажах живут Петя и Коли? 
8. Толя ниже Юры, а Володя с Мишей одинаковые по росту. Юра ниже Миши. Кто выше — Толя или Володя? Кто ниже — Юра или Володя? 
9. В одну из недель в кинотеатре показали 9 новых кинокартин. Был ли на этой неделе такой день, когда показали сразу 2 или 3 новые картины? 
«Викторина» – произошло от латинского слова «виктория» - победа, одна из форм внеклассной работы по математике. Предлагается система вопросов, задач, примеров, доступных данной группе. Организация викторины требует не так уж много времени. Викторины проводятся с целью повышения интереса учащихся к математике. 
III класс 
1. Во сколько раз больше число, выраженное четырьмя единицами 5го 
разряда, чем число, выраженное четырьмя единицами разряда? (2 очка.) 
2. На сколько единиц больше наименьшее шестизначное число, чем 
наибольшее пятизначное число? (1 очко.) 
3. Как изменится разность двух чисел, если из вычитаемого вычесть 5 
единиц, а к уменьшаемому столько же единиц прибавить? (2 очка.) 
4. Задача (решить способом составления уравнения). 
На пришкольном участке росло 30 кустов смородины, расположенных 
рядами, по 6 кустов в каждом. Когда школьники собрали ягоды с 
нескольких кустов, то осталось собрать ягоды еще с 12 кустов 
последних рядов. Со скольких рядов с кустами смородины были 
собраны ягоды? (3 очка.) 
5. Начертить круг радиусом 2 см, затем начертить квадрат так, чтобы круг 
находился внутри его и касался сторон. Вычислить периметр квадрата и 
его площадь. (2 очка.) 
6. Найти все цифры, пропущенные в примере: 
3 * 5 - * 3 * = 137 (2 очка) 
7. При каких значениях буквы х верно неравенство: 
х : 6 8. При каких значениях букв выражение c - b имеет наибольшее значение 
и при каких значениях букв наименьшее значение? (2 очка). 
Загадки. 
Служили и служат увлекательным материалом для размышления. Загадки – это своеобразное логические задания на выявления предмета по некоторым предметам. 
Загадки. 
1.Одна нога в шапке, а головы нет. Что это такое? (Ответ: гриб.) 
2. Штучка-одноручка, носик стальной, а хвостик льняной. Что это? (Ответ: игла.) 
3. Под двумя дугами 
Два яблока с кругами. Что это? (Ответ; брови и глаза.) 
4. Когда сухо— клин, 
Когда мокро — блин. 
Одна нога— и та без сапога. Что это? (Ответ: зонт.) 
5. Две они кленовые, Подошвы — двухметровые. 
На них поставишь две ноги— по большим снегам беги. (Ответ: лыжи.) 
6. Возле елок 
Из иголок 
Летним днем 
Построен дом. 
За травой не виден он, 
И жильцов в нем — миллион. (Ответ: муравейник.) 
7. Под крышей - четыре ножки, а на крыше—суп да ложки. Что это такое? (Ответ: стол.) 
8. Два брюшка, четыре ушка. Что это такое? (Ответ: подушка) 
9. Шестиногая на потолке, а восьминогий ждет ее в уголке. Кто это? (Ответ: муха и паук.) 
Ребусы – загадка, в которой искомое слово или фраза изображены 
комбинацией фигур, букв, знаков. 
Занимательная математика может использоваться в начале урока, в конце, в минуты отдыха, на занятиях кружка «Решение нестандартных задач». Умело подобранные задания повышают интерес детей к математике. Для возбуждения и поддержки интереса задания должны соответствовать следующим условиям: 
- быть непохожими на обычные математические задания, предлагаемые на уроках; 
- смысл заданий должен быть понятен детям; 
- решение задания должно быть доступно каждому из присутствующих ребят; 
- ответы должны получаться быстро, вычисления должны выполняться только устно. 
Минуты занимательной математики должны проводиться систематически, запланированы учителем в связи с поставленной целью урока. 

Заключение 
Ребенок – не кувшин, который надо наполнить, а лампада, которую надо зажечь. Важным условием развития творческих способностей является настойчивость и инициатива человека, без чего не может быть поиска. Исследования, проводимые в этом направлении, позволяют указать основные условия, необходимые для развития творческих способностей школьников. 
-раннее начало (рисование, лепка, конструктор); 
-окружение ребенка такой средой, такой системой отношений, которые бы
стимулировали самую раннюю творческую силу; 
-максимальное напряжение сил, то есть ребенок должен добираться до потолка своих возможностей и постепенно поднимать этот потолок; 
-большая свобода в выборе деятельности, в чередовании дел; 
-умная помощь взрослых; 
-эмоциональная сторона дела. 
За годы работы в школе стали для меня принципами, а может и девизом пословицы. 
Кто ищет, тот найдет. 
Под лежащий камень вода не потечет. 
Известный советский писатель Василий Белов писал: «Каждый ребенок хочет играть, то есть жить творчески. Почему же с годами творчество понемногу исчезает из нашей жизни, почему творческое начало сохраняется и развивается не в каждом?» 
Пробудить заложенные в каждом ребенке творческое начало, научить трудиться, помочь понять и найти себя, сделать первые шаги в творчестве для радостной, счастливой и наполненной жизни – к этому и стремимся мы в меру своих сил и способностей, организуя наши уроки. Конечно, эту задачу не под силу решить одному педагогу. Но если каждый из нас задастся этой целью и будет стремиться к нему, то выиграют, в конечном счете, наши дети, наше будущее. 

В нашей жизни все неповторимо, 
Так ведется издавна, в веках. 
Только лишь одно бесспорно, зримо, 
Кто учил – живет в учениках. 
Учит, значит видит в жизни бег. 
Верю я, что истинный учитель, 
На земле счастливый человек! 

Список использованной литературы.

1. Башмаков М.И., Нефёдова М.Г. «Математика» 1-4 классы. Учебник. Москва: АСТ: Астрель, 2015.

2. Истомина Н.Б.,Нефедова М.Г. Первые шаги в формировании умения решать задачи. Журнал «Начальная школа» №11, 2008г.

3. Левитас Г.Г. Нестандартные задачи по математике. Москва, ИЛЕКСА, 2017.

4. Пупышева О.Н. Олимпиадные задания. Москва, «ВАКО», 2012

5. http://nsportal.ru/nachalnaya-shkola/raznoe/

10