Макет математического уголка

МАКЕТ «МАТЕМАТИЧЕСКИЙ УГОЛОК"

Зоны оформления:

1. Стена (где будет расположено название уголка занимательной математики в виде больших красочных букв, красочные иллюстрации математического содержания)

2. Полки и шкафчики (где будет храниться весь дидактический материал, который должен быть доступным для детей)

3. Стол (где ребёнок один, вместе со взрослым или со сверстниками сможет работать)

В математическом уголке хранят и по необходимости выдают различные инструменты (измерительные, чертежные), материалы (бумага, краски, кисточки и др.), отдельные наглядные пособия для внеклассной работы.

В уголке вывешиваются красочно оформленные плакаты с сообщениями о викторинах, олимпиадах, об учениках класса, ставших победителями математических соревнований, победителях в математических соревнованиях в классе и др.

Содержание математического уголка в начальной школе:

• Математические логические, развивающие и интеллектуальные игры: «Подбери по цвету», «Развивающее лото»;

• Дидактические игры с наглядным материалом, знакомые детям по занятиям: «Где больше», пазл с примерами, журналы «Школа малышей», «Математика», «Весёлый счёт»;

• Математические развлечения: игры-головоломки, счёты, «Матрёшка», «Пирамидка»;

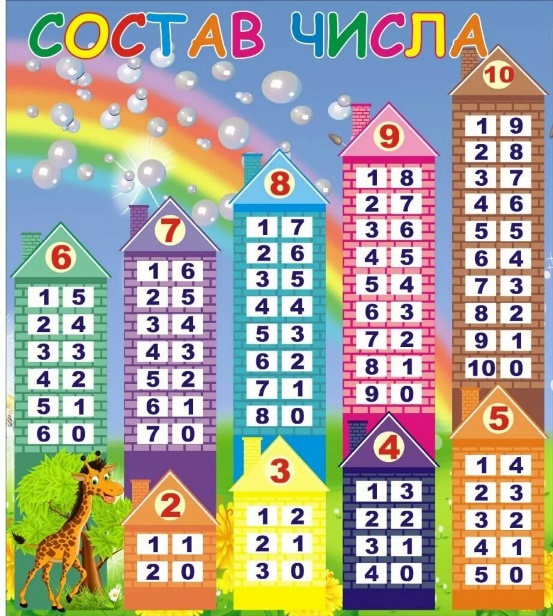
• Дидактические пособия (модели, плакаты «Состав чисе», «Таблица сложения», «Меры величин», «Компоненты сложения», «Компоненты вычитания», «Меры времени», вкладыши и т.д.;

• Настольные игры: «Цифры», «Домино», «Математика», «Время», «Учимся считать», «Сколько не хватает» и т.д.;

• Дополнительный рабочий материал (набор магнитных цифр, счётный материал, касса счётных материалов, цветные карандаши, ручки, фломастеры, веер, бумага и т.д.).

ЗАНИМАТЕЛЬНЫЕ ЗАДАЧИ

1. Шесть пирожных разделили между братьями и сестрами так, что у братьев их оказалось на два меньше, чем у сестер. Сколько у кого?

Решение. Задача может быть решена угадыванием. Однако желательно дать и решение с вопросами. Этого можно добиться, если нарисовать два отрезка, один из которых на две клетки больше другого. Как узнать, сколько клеток должно быть в каждом отрезке? Сумма этих трех отрезков должна равняться 6 клеткам. Значит, сумма двух равных отрезков равна 6 – 2 = 4, а каждый из них 2. Когда учащимся покажется, что это рассуждение ими понято, нужно записать его по вопросам и действиям. Нужно подсказать первый вопрос:

1) Сколько было бы пирожных, если бы у сестер было столько же, сколько у братьев? 6 – 2 = 4.

2) Сколько было пирожных у братьев? 4 : 2 = 2.

3) Сколько было пирожных у сестер? 2 + 2 = 4 (или 6 –2 = 4).

Ответ: у братьев 2, у сестер 4.

2. Ваня живет в 12-этажном доме, на 9 этаже, если считать сверху. На каком этаже живет Ваня?

Решение. Можно нарисовать дом, а можно решить задачу и без рисунка, узнав, сколько этажей дома находится ниже Вани (12 – 9 = 3).

Ответ: На 4 этаже.

3. В коробке лежит 15 шариков: черных, белых и красных. Красных шариков в 7 раз больше, чем белых. Сколько в коробке черных шариков?

Решение. Белых шариков не может быть больше одного, так как если бы их было хотя бы 2, то красных шариков было бы не меньше 14, а шариков всего 15. Значит, белый шарик всего один, а красных в семь раз больше, то есть семь. Черных шариков 15 – (1 + 7) = 7.

4. Пес Тузик на 6 кг тяжелее кота Барсика, а Барсик втрое легче Тузика. Сколько весит Барсик?

Решение можно сопроводить рисунком. 6 : 2 = 3 (кг) – вес Барсика.

Ответ: 3 кг.

5. Расшифруй предложение, в котором каждая буква заменена ее номером в русском алфавите и все слова написаны слитно:

(15)1(14)(17)6(19)(15)(33)(19)(20)(18)(16)(10)(20)(30)

(10)8(10)(20)(30)(17)(16)(14)(16)4(1)6(20).

Ответ: Нам песня строить и жить помогает.

6. Придумай возможное продолжение этой последовательности чисел: 1, 1, 2, 3, 5, …

Решение. 1 + 1 = 2; 1 + 2 = 3; 2 + 3 = 5. Одно из правил, по которому может быть составлена эта последовательность, таково: первые два числа – единицы, а каждое число, начиная с третьего, равно сумме двух предыдущих чисел.

Ответ: Возможно такое продолжение: 8, 13, 21, …

7. У Васи и Коли вместе 15 марок. Вася подарил из них Коле 2 марки. Сколько стало у них вместе марок после этого?

Это – задача-шутка. Марок осталось, сколько было, – 15.

8. Какой вес можно взвесить гирями 1 кг, 2 кг и 4 кг на чашечных весах, если гири можно класть на одну чашу весов?

Решение можно сопроводить рисунками.

Ответ: Любой вес от 1 до 7 кг.

9. В коробке лежит 4 шарика: черных, белых и красных. Красных шариков столько же, сколько белых и черных вместе. Сколько черных шариков в коробке?

Решение. Красные шарики составляют половину всех шариков, то есть их 2. Черных и белых шариков вместе 2. Значит, их по одному каждого цвета.

Ответ: Черных 1, белых 1, красных 2.

10. У котенка на лапе 5 когтей, а у цыпленка 4. Во дворе находятся 10 котят и цыплят, а когтей у всех у них 104. Сколько котят во дворе?

Решение.

1) Сколько когтей у одного котенка?

5 х 4 = 20 (к.).

2) Сколько когтей у одного цыпленка?

4 х 2 = 8 (к.).

3) Сколько было бы когтей, если бы во дворе было 10 цыплят?

8 х 10 = 80 (к.).

4) Сколько когтей "лишние"?

104 – 80 = 24 (к.).

5) На сколько когтей у одного котенка больше, чем у одного цыпленка?

20 – 8 = 12 (к.).

6) Сколько было котят?

24 : 12 = 2 (кот.).

Ответ: 2 котенка.

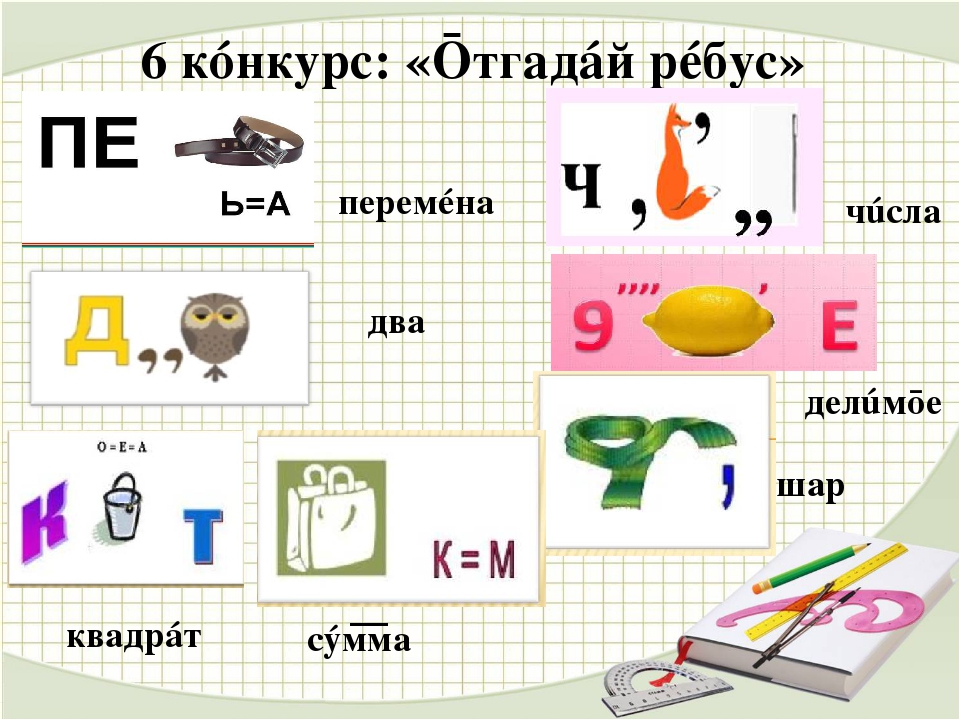
МАТЕМАТИЧЕСКИЕ РЕБУСЫ

МАТЕМАТИЧЕСКИЕ КРОССВОРДЫ

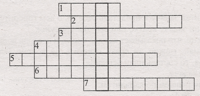
По горизонтали: 3. Период в 100 лет. 4. Результат сложения. 6. Четырехугольник, у которого все углы прямые. 8. Что получится, если к разности прибавить вычитаемое? 9. Результат вычитания.

По вертикали: 1. Прямоугольник, у которого все стороны равны. 2. Промежуток времени, равный 60 минутам. 4. Что получится, если из суммы вычесть слагаемое. 5. Прибор для измерения длины предметов. 7. Промежуток времени, равный 12 месяцам.

Ответы:

По горизонтали: 3. Век. 4. Сумма. 6. Прямоугольник. 8. Уменьшаемое. 9. Разность.

По вертикали: 1. Квадрат. 2. Час. 4. Слагаемое. 5. Линейка. 7. Год.

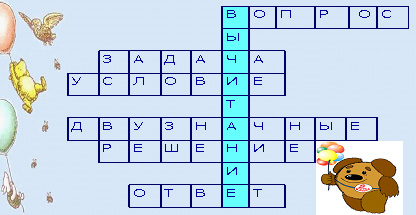
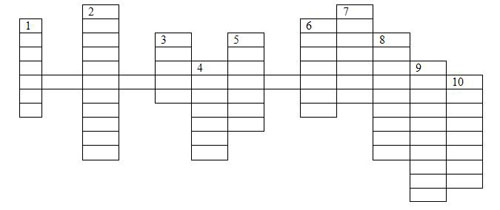
1. Часть задачи, в которой сообщается о том, что нужно узнать (вопрос).

2. Рассказ, в котором есть числа и вопрос, на который нужно ответить, выполнив арифметические действия (задача)

3. Часть задачи, в которой рассказывается, что в ней известно (условие)

4. Как называются числа 11, 23, 48, 97 (двузначные).

5. Часть задачи, в которой находят ответ на вопрос задачи (решение).

6. Искомое число в задаче (ответ).

7. Арифметическое действие (вычитание).

1. Результат действия сложения. (Сумма.)

2. Название компонента действия умножения. (Множитель.)

3. Фигура, полученная пересечением двух прямых. (Угол.)

4. Результат действия деления. (Частное.)

5. Число, полученное при умножении. (Произведение.)

6. Очень плохая оценка знаний. (Единица.)

7. Действие, обратное сложению. (Вычитание.)

1. Прямоугольник, у которого все стороны равны (квадрат);

2. Если к значению разности прибавить вычитаемое, то получим…(уменьшаемое);

3. Стороны прямоугольника попарно…(равны);

4. Великий философ, его именем назвали таблицу умножения (Пифагор);

5. Чтобы узнать, на сколько одно число больше или меньше другого, надо из большего меньшее…(вычесть);

6. Прямая, которая имеет начало и конец, называют…(отрезок);

7. В выражениях со скобками в первую очередь выполняем действие в…(скобках);

8. Чтобы узнать, во сколько раз одно число больше или меньше другого, надо…(разделить);

9. Царица наук (математика);

10. Результат деления называют значение…(частного).

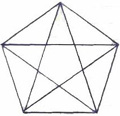
МАТЕМАТИЧЕСКИЕ ГОЛОВОЛОМКИ

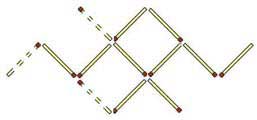
1. Сколько треугольников изображено в геометрической фигуре? (35)

2. В три хода.

Положить на стол 3 кучки спичек. В одну кучку положить 11 спичек, в другую - 7, и в 3-ью - 6. Перекладывая спички из любой кучки в любую другую, надо сравнять все три кучки, чтобы в каждой было по 8 спичек.

Это возможно, так как общее число спичек - 24 - делится на 3 без остатка. При этом необходимо соблюдать правило: к любой кучке необходимо добавлять ровно столько спичек, сколько в ней есть. Например, если в кучке 6 спичек, то и добавить к ней можно только 6, если в кучке 4 спички, то и добавить к ней можно только 4. Задача решается в 3 хода.

Примечание: Вместо спичек могут быть использованы счетные палочки, пуговицы, другие предметы.

Ответ:

1) Из кучки где находится 11 спичек, берем 7 и перекладываем в кучку к 7 спичкам; в первой кучке осталось 4 спички;

2) Из второй кучки, где у нас получилось 14 спичек, берем 6 спичек и перекладываем в 3-тью кучку где имеется 6 спичек. В третьей кучке у нас получилось 12 спичек, во второй - 8 (первый результат);

3) Из третьей кучки, в которой 12 спичек берем 4 спички и перекладываем их к 4-ем спичкам, оставшимся в первой кучке. Во всех трех кучках получилось одинаковое число спичек - по 8.

3. Раздробить на части.

Раздробите число 45 на четыре части так, что если к первой части прибавить 2, от второй отнять 2, третью умножить на 2, а четвертую разделить на 2, то все результаты будут равными.

Ответ: Искомые части 8, 12, 5 и 20.

4. Какой знак надо поставить между написанными рядом цифрами 2 и 3, чтобы получилось число, большее двух, но меньшее трех?

Ответ: Запятую; получится 2,3.

5. Из спичек (счетных палочек) выложена цифра 14. Как превратить ее в цифру 5, переложив только одну спичку (счетную палочку)?

Ответ:

6. Сколько раз можно прочитать слово "ОРХИДЕЯ" в представленной фигуре?

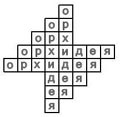
Ответ: 128 раз.

7. Берем 12 спичек (палочек) и выкладываем из них "равенство", как показано на рисунке. Как видите, "равенство" 6 - 4 не может равняться 9. Как переложить одну спичку так, чтобы получилось правильное равенство? Задача решается несколькими способами.

Первый ответ:

Второй ответ:

8. На рисунке изображен «жук» из 10 спичек. Необходимо изменить направление движения жука, переложив всего три спички (счетные палочки).

Ответ:

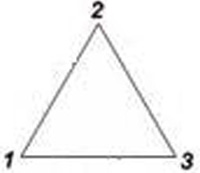
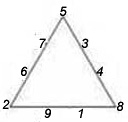
9. В вершинах треугольника помещены числа 1, 2 и 3. Разместите числа 4, 5, 6, 7, 8 и 9 по сторонам треугольника (по две цифры на каждой стороне) так, чтобы сумма всех чисел вдоль каждой стороны треугольника равнялась 17. Это нетрудно, так как известны числа в вершинах треугольника.

А попробуйте разместить числа 1, 2, 3, 4, 5, 6, 7, 8 и 9 вдоль сторон треугольника (по четыре цифры на стороне) так, чтобы сумма чисел на каждой стороне треугольника равнялась 20.

Числа в вершинах треугольника будут другие. В первом и втором случаях числа не повторяются и должны размещаться только по одному разу. Расположение чисел по сторонам треугольника может быть разнообразным.

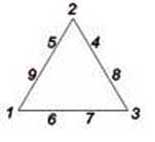
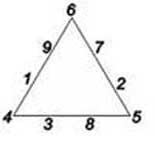
Ответ:

10. На рисунке расположено 9 точек. Необходимо перечеркнуть их четырьмя прямыми линиями, не отрывая карандаш от бумаги.