Начальные геометрические сведения. Прямая и отрезок.

ГЛАВА 1. Начальные геометрические сведения.

Геометрия – это раздел математики, изучающий фигуры на плоскости, тела в пространстве, а также их свойства.

В школьном курсе изучаются два раздела геометрии:

• П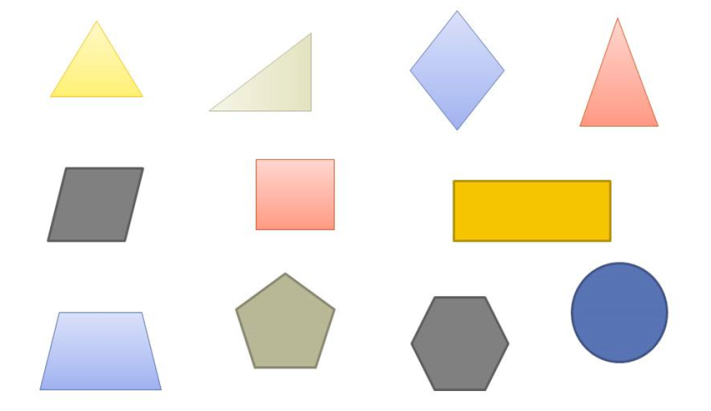 ланиметрия – это раздел геометрии, который изучает фигуры и их свойства на плоскости.

• С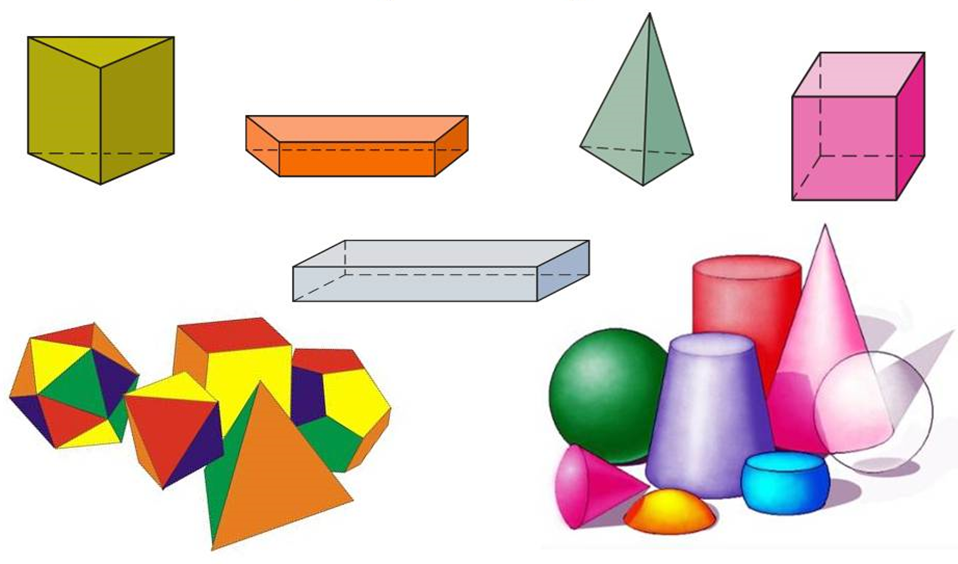 тереометрия - это раздел геометрии, который изучает тела и их свойства в пространстве.

Мы начинаем с изучения планиметрии.

§ 1. Прямая и отрезок.

1. Точки, прямые, отрезки.

Темнота. Никого и ничего. А так бывает? Если существую я, значит, существует ещё кто-то, или, по крайней мере, что-то. Напрягаю зрение и, кажется, что-то вижу. О! Да! Вижу! Вижу! Маленькая, ничем неприметная, совсем одинокая ТОЧКА!

- Как зовут тебя, долгожданная незнакомка?

- Да, как хочешь! Хочешь – буду А, а не понравится, буду В, С, D. У меня может быть много имён, только не называй меня Ц, Ы, Й, Щ, … . Догадался почему?

- Ну, наверное, догадался. Твои имена латинские?

- Супер!

- Я буду звать тебя А.

- Замётано! Как мне называть тебя?

- Зови меня просто: Ученик.

- Тебе не тоскливо быть одной?

- А я не одна. Нас много, очень много.

Что-то мелькнуло справа, слева, впереди, и даже, кажется, сзади. Очень медленно и плавно становилось светлее. И, наконец, всё пространство вокруг заполнилось такими же маленькими, сияющими точками. Даже под ногами их было бесконечное множество! От этого зрелища захватило дух! Это же целая ВСЕЛЕННАЯ!

- Как же вас много! Ну, ладно, а какой смысл в таком количестве? Дальше-то что? Что вы можете?

- Смотри сам.

И тут точки начали передвигаться, сближаться, выстраиваться по какому-то, одним им известному, закону. У меня на глазах совершалось почти чудо. Это было так просто и, в то же время, так завораживающе! Произошла трансформация и я увидел, на что способны эти маленькие, но, как оказалось, очень могущественные ТОЧКИ!

- Фантастика! А что это?

- Говоря на твоём языке, это геометрические фигуры, состоящие из бесконечного множества точек.

- И как эти фигуры называются?

- ПРЯМЫЕ.

- Они же разные, как вы их отличаете?

- У каждой прямой есть имя. Оно образуется от имени двух любых точек, из которых состоит прямая. Например, АВ или ВА.

И тут начался какой-то шум, недовольные возгласы. Точки что-то самозабвенно обсуждали.

- Что случилось?

- Прямые заявили свои права на самостоятельность и хотят иметь другие имена.

- Есть варианты?

- Да, они предлагают называться одной буквой.

- Но ведь одной буквой называетесь вы, точки!

- Есть компромисс! Пусть у них будет маленькая буква.

- Прямые, вы согласны?

- Единственно правильное решение!

- Ну, так тому и быть. Тогда мы будем называть вас либо АВ (ВА), либо а.

Так, наверное, начинается жизнь любой Вселенной. Из очень маленького получается что-то большое. Ну, или, не очень большое.

- А что получится, если на пути прямой встанет какая-нибудь весомая точка?

- Это будет часть прямой, ограниченная одной точкой.

- И как мы её назовём?

- Можно назвать её ПОЛУПРЯМОЙ, потому что она часть прямой, а можно назвать ЛУЧОМ, потому что она похожа на луч солнца.

- Мне кажется, что оба названия логичны и имеют право на существование.

- Принято.

- Какие имена дадим полупрямым?

- Поскольку полупрямая – это часть прямой, то пусть называется также. Либо двумя заглавными буквами, либо одной маленькой буквой.

- Ну, тогда первая буква должна означать начало луча, а маленькая буква должна находиться на продолжении полупрямой. Т.е. АВ или а.

- Логично.

- Ну, а если на пути прямой встанут две точки?

- Тогда от прямой будет отрезан кусочек. И эту часть прямой, ограниченную двумя точками, будем называть ОТРЕЗОК.

- Дай догадаюсь! Имя у отрезка будет однозначно состоять из двух заглавных букв, потому что они обозначают точки (концы отрезка)! Верно?

- Ты делаешь успехи!

Я стал осознавать, что включился в создание этой Вселенной. И мне было приятно, что могу дать ей имя. Я назвал её ГЕОМЕТРИЧЕСКОЙ ВСЕЛЕННОЙ. Фантазия моя разыгралась не на шутку! Ведь сколько всего можно в ней построить! Какие неограниченные возможности!

Итак, подведём итоги.

1. Простейшей геометрической фигурой является точка. Точка обозначается заглавной латинской буквой.

2. Прямая – это геометрическая фигура, состоящая из бесконечного множества точек. Прямые обозначаются либо двумя заглавными латинскими буквами, либо одной маленькой латинской буквой.

3. Отрезок – это часть прямой, ограниченная двумя точками. Отрезок обозначается двумя заглавными латинскими буквами, определяющими его начало и конец.

Между всеми фигурами существует определённое правило взаимного расположения и зависимости друг от друга. Простейшие правила, которые не нужно доказывать, они очевидны, называются аксиомами.

Аксиома I. Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей. Через любые две точки плоскости можно провести прямую, и только одну.

Аксиома II. Из трёх точек, лежащих на прямой, одна и только одна лежит между двумя другими.

Две прямые либо имеют одну общую точку (тогда говорят, что они пересекаются), либо не имеют общих точек (тогда говорят, что они параллельны), либо имеют бесконечно много общих точек (тогда они совпадают).

1. П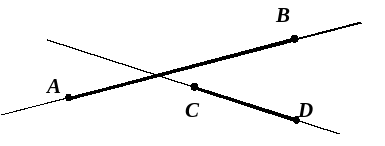 ересекаются ли отрезки AB и CD?

2. Пересекаются ли прямые AB и CD?

3. Отметьте точку М так, чтобы она лежала на прямой CD, но не лежала ни на отрезке AB, ни на отрезке CD.

4. Отметьте точку N, которая лежит на прямой CD между точками A и B. Как вы назовёте такую точку?

1. П ересекает ли прямая KL отрезок EF?

2. Пересекает ли прямая KL прямую EF?

3. Отметьте точку А, которая лежит на прямой EF, но не лежит на прямой KL.

4. Существуют ли точки, которые одновременно лежат на отрезке EF и прямой LK?

1. С колько существует различных отрезков с концами в точках A, B, C и D?

2. Пересекаются ли прямые AB и CD?

3. Какая из точек, A или D, лежит между точками B и C?

4. Отметьте точку М, которая лежит на прямой AD, но не лежит на отрезке BC.

5. Проведите прямую, проходящую через точку Е, которая пересекает прямые AB и BC, но не пересекает отрезок AD.

1. С колько существует различных отрезков с концами в точках E, F, M и N?

2. Пересекаются ли прямые EN и FM?

3. Какая из точек, A или N, лежит между точками E и F?

4. Отметьте точку B, которая лежит на отрезке MN, но не лежит на прямой EF.

5. Проведите прямую, проходящую через точку A, которая пересекает прямые EF и MN, но не пересекает отрезок FM.

1. Начертите две пересекающиеся прямые и расположите на них два отрезка, не имеющие общих точек.

2. Сколько точек надо взять между точками A и B, чтобы вместе с отрезком AB получилось шесть различных отрезков?

3. Даны отрезок AB, точка E, не лежащая на прямой AB, и точка C, лежащая на прямой AB. Каково взаимное расположение прямой EC и отрезка AB?

4. М ожно ли провести прямую, не проходящую через точку A, так, чтобы она пересекала одновременно прямые AB, AC и AD.

1. Начертите две пересекающиеся прямые и расположите на них два непересекающиеся отрезка так, чтобы точка пересечения прямых принадлежала одному из них.

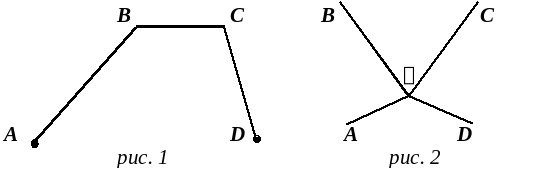
2. Проведите прямую, которая пересекает некоторые из указанных на рис. 1 отрезков, так, чтобы вместе с данными отрезками образовалось шесть отрезков.

3. Дана прямая EF, A∉EF, B∉EF. Может ли прямая AB не пересекать отрезок EF?

4. Может ли прямая, не проходящая через точку O, одновременно пересекать прямые OA, OB, OC и OD (рис. 2)?

1. Сколько различных прямых можно провести через 4 точки? Сделайте чертежи.

2. По рисунку определите число отрезков с концами в обозначенных точках.

1. Сколько точек пересечения могут иметь четыре попарно пересекающиеся прямые? Для каждого случая сделайте рисунок.

2. По рисунку определите число отрезков с концами в обозначенных точках.

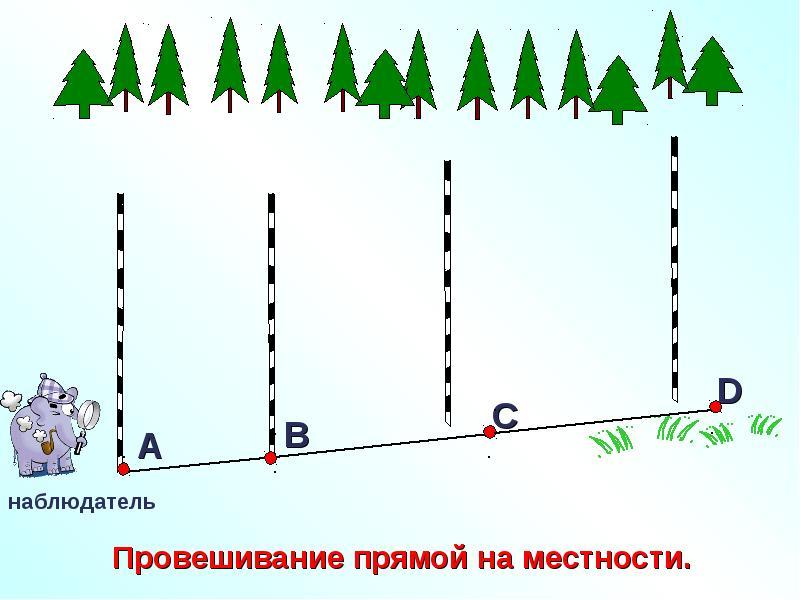
2. Провешивание прямой на местности.

Знание геометрии, и умение применять эти знания на практике, полезно в любой профессии. Традиционно построения на местности производят для съёмки плана земельного участка и для закладки фундаментов. Однако, такие знания бывают нужны и в других областях деятельности.

Можно подумать, что работа на местности ничем не отличается от работы циркулем и линейкой на бумаге. Но это не так. На местности расстояния между точками довольно велики и нет таких линеек и циркулей, которые смогли бы помочь в измерении этих расстояний. Таким образом, построения на местности имеют свою специфику.

• Во-первых, все прямые не проводятся на земле, а прокладываются, т.е. отмечаются, например, колышками (вехами) достаточно густая сеть точек. Прокладку прямых на местности называют провешиванием.

• В о-вторых, запрещается при построениях проводить какие-либо дуги. Поэтому, расстояния между колышками (вехами) измеряются шагами, или любыми, подходящими для этих целей, предметами.

Веха – это вертикальная прямая жердь, которая устанавливается для обозначения точки на местности; имеет длину около 2 м; заострена на одном конце, чтобы её можно было воткнуть в землю.

Чтобы веха стояла прямо, применяют какой-нибудь отвес (грузик, подвешенный на нитке).

Провешивание широко используется при вырубке лесных просек, при прокладывании трассы шоссейной или железной дороги, линий высоковольтных передач.

7