Обобщающий урок по теме «Четырёхугольники»
(геометрия – 8)
Синаева Роза Ивановна
МАОУ «СОШ №19»
Пояснительная записка:
Данная разработка урока по геометрии предназначена для обучающихся 8 класса. Рассчитана на 2 урока.
Цель урока:
Образовательная: формирование умений применять полученные ранее знания, систематизировать и ориентироваться в них, применять свойства четырехугольников при решении задач.
Воспитательная: формирование интереса к познавательному процессу, навыков самоконтроля и взаимоконтроля.
Развивающая: развитие наблюдательности, памяти, логического мышления, умения рассуждать и аргументировать свои действия.
Тип урока: комбинированный.
Оборудование: Карточки с заданиями.
План урока:
Организованный момент.
Загадки по теме «Четырехугольники».
Самостоятельная работа в парах.
«Чёрный ящик».
Физминутка.
Решение задач.
«Встали-сели».
Практическая работа исследовательского характера.
Закрепление теоретического материала.
Практическая работа.
«Угадай-ка».
Домашнее задание.
Итог урока «Сказка».
Содержание.
1. Организационный момент.
Приветствие учителя.
Добрый день! Добрый час!
Как я рада видеть вас.
Прозвенел уже звонок
Начинается урок.
Улыбнулись. Подровнялись.
Друг на друга поглядели
И тихонько дружно сели.
2. Загадки по теме «Четырёхугольники».
2.1 Хоть стороны мои попарно и равны, и параллельны
Всё ж я в печали, что не равны мои диагонали
Да и углы они не делят пополам.
Но всё ж скажи, дружок, кто я? (параллелограмм).
2.2 Хочу сказать я, хоть меня не называли
И у меня равны диагонали.
И хоть я не зовусь квадратом
Он мне приходится родимым братом. (прямоугольник)
2.3 Мои хоть не равны диагонали,
По значимости всем я уступлю едва ли,
Ведь под прямым углом они пересекаются,
И каждый угол делят пополам,
И очень важная фигура я, скажу я вам. (ромб)
2.4 Знаете ли вы меня, хочу проверить
Любую площадь я могу измерить,
Ведь у меня четыре стороны
И все они между собой равны.
И у меня ещё равны диагонали,
Углы они мне делят пополам,
И ими на части равные разбит я сам. (квадрат)
Учитель: Ребята! Сегодня на уроке вы должны показать:
свои знания по КАКОЙ теме? «Четырехугольники»;
как вы умеете по виду определять четырехугольники;
умение применять полученные знания на практике.
3. Самостоятельная работа в парах.
Ученики в тетрадях записывают только ответы.
1) Четырёхугольник, у которого диагонали пересекаются и точкой пересечения делятся пополам, является ……..(параллелограммом)
2) Четырёхугольник, у которого только две стороны параллельны, называется ……… (трапецией)
3) Параллелограмм, у которого диагонали равны, является… (прямоугольником)
4) отрезок, соединяющий две несоседние вершины n-угольника, называется …..(диагональю)
5) если диагонали ромба равны, то он является ….(квадратом);
6) параллельные стороны трапеции называются …….(основаниями)
7) сумма длин всех сторон n-угольника называется …..(периметром)
Ученики сверяют свои ответы с эталонными (на слайде).
4. «Чёрный ящик»
Выходит к доске 1 ученик, вынимает из черного ящика карточку и выполняет устно задание, написанное на ней.



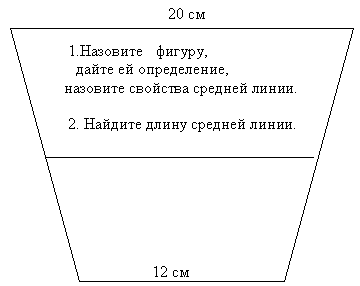

Физминутка
Учитель говорит и показывает движение, ученики повторяют движение
Я – человек (показать рукой на себя)
Всегда готов встать рядом (шаг в сторону)
Или чуть впереди (шаг вперед)
Протянуть руку помощи (протянуть руку вперед)
Легко нагнуться к малому или слабому (наклониться вниз)
Подставить плечо под груз тревог и забот (поднимаем плечи)
Обернуться к отставшим (поворот назад)
Балансировать между желаниями и возможностями (наклоны в стороны)
Перепрыгнуть через усталость и боль (прыжок вперед)
Подняться после неудачи (присесть и встать)
Пронести через всю жизнь дружбу и любовь (обнять себя)
Дотянуться до мечты (подтянуться вверх)
Глубоко вздохнуть по несбывшемуся (глубокий вдох)
И верить в победу!
6. Применяем знания для решения задач на тему «Четырехугольники».
Задача №1. Разность углов, прилежащих к одной стороне параллелограмма, равна 40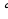 . Найдите меньший угол параллелограмма. Ответ.
. Найдите меньший угол параллелограмма. Ответ. 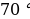 .
.
(Что показывает разность углов? Что мы знаем об углах, прилежащих к одной стороне параллелограмма?)
Задача №2. Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 75° и 50°. Найдите меньший угол параллелограмма. Ответ. 550
Задача №3. Сторона ромба равна 34, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков? Ответ. 17 и 17.
Задача №4. Периметр параллелограмма равен 82. Одна сторона параллелограмма на 29 больше другой. Найдите меньшую сторону параллелограмма. Ответ. 6.
(Что мы знаем о противоположных сторонах параллелограмма?)
7. «Встали-сели».
(Если высказывание истинно – встаем, если ложно- сидим).
1. Если в четырехугольнике диагонали равны и перпендикулярны, то этот четырехугольник квадрат. (нет)
2. Если в четырехугольнике две стороны параллельны, то этот четырехугольник – параллелограмм. (нет)
3. Если диагонали параллелограмма делят его угол пополам, то этот параллелограмм – ромб. (да)
4. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник – параллелограмм. (да)
5. Диагонали ромба в точке пересечения делятся пополам. (да)
6. Если в четырехугольнике два угла – прямые, то этот четырехугольник – параллелограмм. (нет)
7. Диагонали прямоугольника перпендикулярны. (нет)
8. Если сумма трех углов выпуклого четырехугольника равна 200о, то четвертый угол равен 160о. (да)
9. Сумма двух противоположных углов параллелограмма равна 180о. (нет)
10. Если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник. (да)
11. Если один из углов параллелограмма равен 60о, то противоположный ему угол равен 120о. (нет)
12. Если один из углов, прилежащих к стороне параллелограмма, равен 50о, то другой угол, прилежащий к той же стороне, равен 50о. (нет)
13. Диагонали параллелограмма делят его углы пополам. (нет)
14. Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм — квадрат. (да)
15. Если один из углов параллелограмма равен 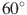 , то противоположный ему угол равен
, то противоположный ему угол равен  . (нет)
. (нет)
16. Если один из углов параллелограмма прямой, то и остальные его углы прямые. (да)
17. В любом ромбе все стороны равны. (да)
18. У четырехугольника, все стороны которого равны, диагонали перпендикулярны. (да)
19. Диагонали любого прямоугольника равны. (да)
20. Ромб не является параллелограммом. (нет)
21. Существует параллелограмм, который не является прямоугольником. (да)
22. Не существует прямоугольника, диагонали которого взаимно перпендикулярны. (нет)
8 . Практическая работа исследовательского характера.
. Практическая работа исследовательского характера.
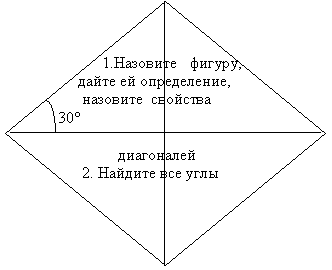
В школьном курсе геометрии изучаются только 5 видов четырехугольников. Сегодня на уроке предлагаю выйти за рамки школьной программы и познакомиться с еще одним четырехугольником. Для этого мы проведем небольшое исследование.
Перед вами четырехугольник, который называется ромбоид или дельтоид. Ваша задача: изучить свойства данного четырехугольника
(1ряд изучает стороны, 2 ряд – углы, 3 ряд - диагонали).
Давайте обсудим ваши предположения и запишем его определение и свойства в тетрадь.
Ромбоид ( дельтоид ) – это четырехугольник, у которого две стороны, прилежащие к одной вершине, попарно равны.
Свойства:
Меньшая диагональ точкой пересечения делится пополам.
Диагонали перпендикулярны.
Большая диагональ является биссектрисой углов.
Меньшая диагональ делит его на два равнобедренных треугольника.
9. Закрепление теоретического материала.
9.1 Повторим определения
Параллелограмм с равными сторонами и взаимно перпендикулярными диагоналями…
Параллелограмм с прямым углом …
Параллелограмм с равными сторонами…
Четырехугольник, у которого две противоположные стороны параллельны и равны…
Ромб с прямым углом…
Параллелограмм с равными сторонами…
Четырехугольник, у которого только две стороны параллельны…
Выбрать нужное
Параллелограмм
Прямоугольник
Ромб
Квадрат
Трапеция
9.2 Свойства диагоналей
Диагонали ромба…
В прямоугольнике диагонали точкой пересечения …
Диагонали равнобедренной трапеции…
Общее свойство диагоналей прямоугольника и квадрата…
Выбрать нужное
равны
пересекаются
делятся пополам
перпендикулярны
делят углы пополам
9.3 Свойства углов
В параллелограмме сумма углов 180 градусов
В равнобокой трапеции эти углы равны
В любом параллелограмме эти углы равны
В параллелограмме равны не только углы, но и …
В прямоугольной трапеции есть такие углы
У квадрата и прямоугольника углы…
Выбрать нужное
Все углы равны
Прилежащие к одной стороне
Противоположные
Углы при основании
Прямые углы
Стороны
10. Практическая работа.
«А теперь посмотрим, как свойства и признаки параллелограммов помогут нам решить некоторые практические задачи»
1. Паркетчик, вырезая квадраты из дерева, проверял их так: он сравнивал длины сторон, и если все четыре стороны были равны, то считал квадрат вырезанным правильно. Надежна ли такая проверка?
(Такая проверка недостаточна. Четырехугольник мог выдержать такое испытание, не будучи квадратом, ромб тоже имеет равные стороны)
2. Другой паркетчик проверял свою работу иначе: он мерил не стороны, а диагонали. Если обе диагонали оказывались равными, паркетчик считал квадрат вырезанным правильно. Вы тоже так думаете?
(Эта проверка ненадежна. В квадрате, конечно, диагонали равны, но не всякий четырехугольник с равными диагоналями есть квадрат. Равные диагонали могут быть у прямоугольника и у равнобокой трапеции).
3. Третий паркетчик при проверке квадратов убеждался в том, что все 4 части, на которые диагонали разделяют друг друга, равны между собой. По его мнению, это доказывало, что вырезанный четырехугольник есть квадрат. А по-вашему?
(Этим свойством обладают не только диагонали квадрата, но и диагонали прямоугольника).
11. «Угадай-ка».
Учитель нарисовал на доске четырехугольник и спросил у учеников, что это за фигура?
Иванов сказал, что это квадрат. Петров считает, что это трапеция.
Сидоров ответил, что нарисован ромб. Фёдоров решил, что это параллелограмм.
Оказалось, что из четырёх ответов только три были верные, а один - неверный.
Что за фигуру изобразил учитель?
Ребята, вы замечательно справились с поставленными задачами.
12. Домашнее задание.
Решить задачи, в прикрепленном файле в электронном журнале.
Один из углов параллелограмма в два раза больше другого. Найдите меньший угол.
Ответ. 60
(О каких углах идет речь в задаче?)
Один из углов параллелограмма на 46о больше другого. Найдите больший из углов.
Ответ. 67
(О каких углах идет речь в задаче?)
3. Найдите меньшую диагональ ромба, стороны которого равны 49, а острый угол равен 60о.
Ответ. 49
(На какие треугольники делит меньшая диагональ ромб?)
В параллелограмме АВСD диагональ АС является биссектрисой угла А. Найдите сторону ВС, если периметр АВСD равен 32 см.
Ответ. 8
(Когда в параллелограмме диагональ является биссектрисой угла?)
Сторона ромба равна его диагонали. Найдите больший угол ромба.
Ответ. 120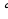
В прямоугольнике угол между диагоналями равен 68о. Найдите угол между диагональю и большей стороной прямоугольника.
Ответ. 34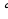
В прямоугольнике диагональ делит угол в отношении 1:2, меньшая его сторона равна 33. Найдите диагональ данного прямоугольника.
Ответ. 66
(Чему равны углы в прямоугольнике? На какие два угла делит диагональ угол? Какое свойство прямоугольного треугольника надо вспомнить?)
Наш урок подходит к концу и наступает момент творчества.
13. Послушайте сказку, которая закончится вопросами.
Собрались все четырехугольники на лесной поляне и стали обсуждать вопрос о выборе своего короля. Долго спорили и не могли прийти к единому мнению. И вот один старый параллелограмм сказал: «Давайте все отправимся в царство четырехугольников. Кто первым придет, тот и будет королем!» Все согласились.
Рано утром отправились в далекое путешествие. На пути фигур встретилась широкая река, которая сказала: «Переплывут меня только те, у кого диагонали пересекаются и точкой пересечения делятся пополам». Часть четырехугольников остались на берегу, а остальные благополучно переплыли и пошли дальше. На пути им встретилась высокая гора, которая сказала, что даст пройти только тем, у кого диагонали равны. Несколько путешественников остались у горы, а остальные пошли дальше. Дошли до большого обрыва, где был узкий, неустойчивый мост. Мост сказал, что пропустит тех, у кого диагонали пересекаются под прямым углом. По мосту прошел только один четырехугольник, который первым добрался до царства и стал королем.
Вопросы:
Кто стал королем? (квадрат)
Кто был основным его соперником? (прямоугольник)
Кто первым вышел из соревнования? (трапеция).













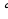 . Найдите меньший угол параллелограмма. Ответ.
. Найдите меньший угол параллелограмма. Ответ.  .
. . Практическая работа исследовательского характера.
. Практическая работа исследовательского характера.









