План-конспект урока алгебры и начал анализа 11 класс
кУРНИК л.м.
Формула перехода
к новому основанию логарифма
Цели: вывести формулу перехода к новому основанию логарифма и сформировать представление о связи логарифмических функций с разными основаниями логарифма; вывести два следствия из указанной формулы; формировать умение использовать формулу перехода для решения задач.
Ход урока
I. Организационный момент.
II. Устная работа.
1. Вычислить.
а) log 2 16; б) 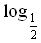 32; в) lg 0,0001;
32; в) lg 0,0001;
г) log 3 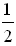 + log 2 18; д) lg 500 – lg 5; е) log 5 254.
+ log 2 18; д) lg 500 – lg 5; е) log 5 254.
2. Замените * соответствующим числом.
а) log * 4 = –2; б) 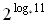 = 11; в) log 2 16* = 20;
= 11; в) log 2 16* = 20;
г) log 2 100 – log 2 * = 1; д) 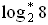 = 81; е)
= 81; е) 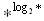 = 1.
= 1.
III. Объяснение нового материала.
1. Актуализация знаний.
Вспоминаем, как связаны графики функций y = f (x), y = f (x) + b,
y = k · f (x), y = f (x + a) и y = f (mx). Механические преобразования предполагают параллельный перенос либо сжатие (растяжение) вдоль осей координат графика исходной функции.
2. На рисунке 215 учебника представлены графики функций y = log 2 x, y = log 3 x. Замечаем, что график функции y = log 2 x получен растяжением графика функции y = log 3 x вдоль оси Oу. Но возможно это только видимость, доказать можно вывод, если верно равенство log 2 x = k · log 3 x, где k – некоторое число. Возникает проблемная ситуация.
3. Для решения поставленной проблемы нам необходима теорема:
log a b = 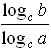 , где a 0, b 0, c 0, a 1.
, где a 0, b 0, c 0, a 1.
Пусть x = log a b, y = log c b, z = log c a, тогда ax = b; cy = b; cz = a, значит, ax = cy. Так как a = cz, то (cz)x = cy, то есть czx = cy. Следовательно, zx = y, то есть x = 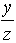 или log a b =
или log a b = 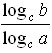
Необходимо провести это доказательство с учащимися в классе. Это позволит еще раз проследить связь взаимообратных функций y = log a x и y = ax.
4. На основании доказанной теоремы мы можем подтвердить свою догадку:
log 3 x = 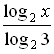 log 2 x = log 2 3 · log 3 x.
log 2 x = log 2 3 · log 3 x.
Значит, коэффициент растяжения k = log 2 3.
5. Предлагаем учащимся самостоятельно вывести следствия из доказанной теоремы. На доску выносим запись всех трех формул.
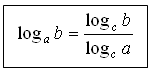
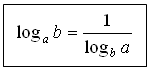
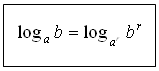
Третью формулу можно также выписать в виде:
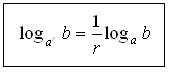
IV. Формирование умений и навыков.
1. Упражнения, выполняемые на этом уроке, направлены как на закрепление самой формулы перехода к новому основанию логарифма, так и на применение её и её следствий для вычисления значений выражений и сравнения чисел. В каждом примере возникает необходимость обоснования выбора нового основания логарифма, к которому осуществляется переход.
2. № 46.1 (а; б), № 46.2, № 46.4 (а; б)
Решение:
№ 46.1.
а) log 2 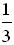 + log 4 9 = log 2
+ log 4 9 = log 2 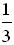 +
+ 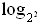 32 = log 2
32 = log 2 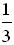 + log 2 3 =
+ log 2 3 =
= log 2 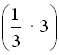 = log 2 1 = 0.
= log 2 1 = 0.
б) 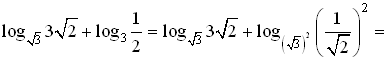
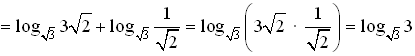 = 2.
= 2.
№ 46.2.
log 2 3 = a.
а) log 3 2 = 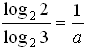 ;
;
б) log 3 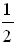 = log 3 2–1 = –1 · log 3 2 = –1 ·
= log 3 2–1 = –1 · log 3 2 = –1 · 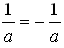 ;
;
в) log 3 4 = log 3 22 = 2 log 3 2 = 2 · 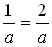 ;
;
г) log 3 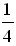 = log 3 4–1 = – log 3 4 =
= log 3 4–1 = – log 3 4 = 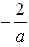 .
.
№ 46.4.
log 2 3 = a.
а) log 4 9 = 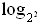 32 = log 2 3 = a;
32 = log 2 3 = a;
б) log 8 18 = log 8 2 + log 8 9 = 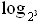 2 +
2 + 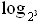 32 =
32 = 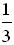 log 2 2 +
log 2 2 +
+ 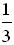 · 2 · log 2 3 =
· 2 · log 2 3 = 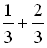 a =
a = 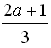 ;
;
в) log 4 81 = log 4 92 = 2 log 4 9 = 2a;
г) log 8 54 = log 8 (18 · 3) = log 8 18 + log 8 3 = 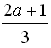 +
+ 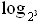 3 =
3 =
= 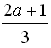 +
+ 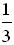 · log 2 3 =
· log 2 3 = 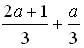 = a +
= a + 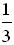 .
.
3. № 46.5 (а; б), № 46.6 (а; б).
Для сравнения чисел необходимо привести логарифмы к одному основанию. Кроме того, необходимо учитывать характер монотонности логарифмической функции.
Решение:
№ 46.5 (а).
log 2 7 и log 7 4.
Приведем второй логарифм к основанию 2.
log 7 4 = 2 log 7 2 = 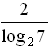 .
.
Оценим полученные выражения:
2 2 7
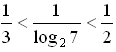 ;
;
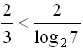
Значит, 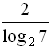 2 7, или log 7 4 2 7.
2 7, или log 7 4 2 7.
№ 46.6 (б).
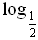 3 и
3 и 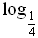 1,5.
1,5.
Имеем: 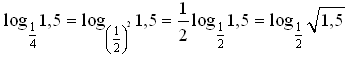 .
.
Функция y = 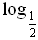 x – монотонно убывает. Так как 3
x – монотонно убывает. Так как 3 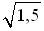 , то
, то 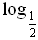 3
3 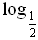
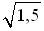 , значит,
, значит, 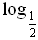 3
3 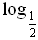 1,5.
1,5.
4. № 46.9 (а; б), № 46.10*.
Для решения упражнений данной группы учащимся необходимо применять все ранее изученные свойства логарифмов и формулу перехода к новому основанию логарифма.
Необходимо побуждать ребят использовать разные следствия теорем о переходе к новому основанию в зависимости от задачной ситуации.
Решение:
№ 46.9
а) 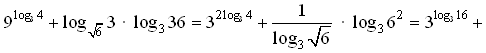
+ 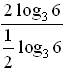 = 16 + 4 = 20;
= 16 + 4 = 20;
б) log 3 8 · log 2 27 – 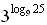 = log 3 23 · log 2 33 –
= log 3 23 · log 2 33 – 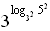 =
=
= 3 · log 3 2 · 3 · log 2 3 – 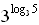 = 9 – 5 = 4.
= 9 – 5 = 4.
Ответ: а) 20; б) 4.
№ 46.10
а) 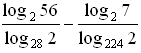 = log 2 56 · log 2 28 – log 2 7 · log 2 224 =
= log 2 56 · log 2 28 – log 2 7 · log 2 224 =
= (log 2 7 + log 2 8)(log 2 4 + log 2 7) – log 2 7 (log 2 7 + log 2 32) =
= (log 2 7 + 3)(2 + log 2 7) – log 2 7 (log 2 7 + 5) = 2 log 2 7 + 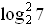 +
+
+ 6 + 3 log 2 7 – 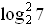 – 5 log 2 7 = 6.
– 5 log 2 7 = 6.
б) 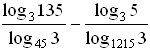 = log 3 135 · log 3 45 – log 3 5 · log 3 1215 =
= log 3 135 · log 3 45 – log 3 5 · log 3 1215 =
= (log 3 5 + log 3 27)(log 3 5 + log 3 9) – log 3 5 (log 3 5 + log 3 243) =
= (log 3 5 + 3)(log 3 5 + 2) – log 3 5 (log 3 5 + 5) = 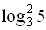 + 2 log 3 5 +
+ 2 log 3 5 +
+ 3 log 3 5 + 6 – 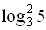 – 5 log 3 5 = 6.
– 5 log 3 5 = 6.
Ответ: а) 6; б) 6.
V. Итоги урока.
Вопросы учащимся:
– Каким образом связаны графики различных логарифмических функций?
– Назовите формулу перехода к новому основанию логарифма.
– Какие следствия существуют из теоремы о переходе к новому основанию логарифма?
Домашнее задание: № 46.1 (в; г), № 46.3, № 46.4 (в; г), № 46.5 (в; г), № 46.6 (в; г), № 46.9 (в; г).






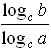 , где a 0, b 0, c 0, a 1.
, где a 0, b 0, c 0, a 1.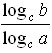
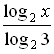 log 2 x = log 2 3 · log 3 x.
log 2 x = log 2 3 · log 3 x.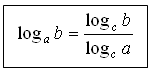
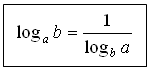
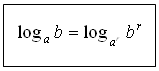
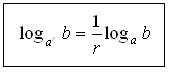
 = log 2 1 = 0.
= log 2 1 = 0.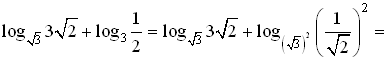
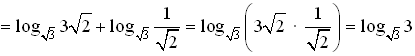 = 2.
= 2.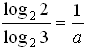 ;
;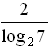 .
.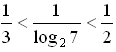 ;
;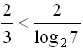
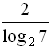 2 7, или log 7 4 2 7.
2 7, или log 7 4 2 7.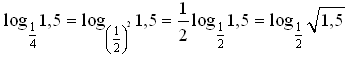 .
.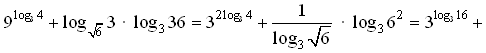
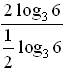 = 16 + 4 = 20;
= 16 + 4 = 20;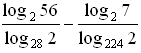 = log 2 56 · log 2 28 – log 2 7 · log 2 224 =
= log 2 56 · log 2 28 – log 2 7 · log 2 224 =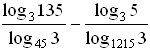 = log 3 135 · log 3 45 – log 3 5 · log 3 1215 =
= log 3 135 · log 3 45 – log 3 5 · log 3 1215 =



















