Дата проведения:
Группа:
Тема: «Логарифмы и их свойства».
Цели и задачи урока:
Образовательная: рассмотреть понятие логарифма числа и свойства логарифмов;
овладеть знаниями и умениями использовать основное логарифмическое тождество, формулы перехода от одного основания к другому в процессе решения упражнений;
Развивающая: развивать мышление учащихся при выполнении упражнений;
научить учащихся определять логарифм числа и его свойства;
Воспитательная: воспитать интерес к уроку.
Тип урока: усвоение новых знаний.
Методическое обеспечение: учебники, индивидуальные карточки.
Литература: учебник математики 10 кл. Колмогоров А.Н.
Ход занятия
1. Организационный момент
Перед началом урока преподаватель проводит проверку подготовленности кабинета к занятию.
Сообщается тема и цель урока.
2. Актуализация знаний
В кратком вступительном слове преподаватель акцентирует внимание студентов о важной
роли логарифмов в курсе математики.
3. Повторение ранее изученного материала
Опрос
Преподаватель задает вопросы:
1) Что такое степень; что такое основание степени; что такое показатель степени.
2) Работа над основными свойствами степеней. Рассмотреть связь между показателями степеней в равенствах

3) Решить устно примеры:

4. Изучение нового материала
План
1. Логарифм числа. Основные свойства логарифмов.
2. Основное логарифмическое тождество.
3. Формула перехода одного основания логарифмов к другому.
Преподаватель излагает новый учебный материал
Логарифм числа
Понятие логарифма числа связано с решением показательных уравнений.
Остановимся на решении двух показательных уравнений. Решение уравнения  не вызывает труда. Так как
не вызывает труда. Так как  то данное уравнение примет вид
то данное уравнение примет вид  Поэтому уравнение имеет единственное решение
Поэтому уравнение имеет единственное решение 
А теперь попробуем решить уравнение  По теореме о корне это уравнение также имеет единственное решение. Однако, в отличие от предыдущего уравнения, это уравнение является иррациональным числом. Докажем, что корень данного уравнения является числом рациональным, т.е.
По теореме о корне это уравнение также имеет единственное решение. Однако, в отличие от предыдущего уравнения, это уравнение является иррациональным числом. Докажем, что корень данного уравнения является числом рациональным, т.е. Тогда выполняется равенство
Тогда выполняется равенство  или
или  Но
Но  в любой натуральной степени будет числом четным, а
в любой натуральной степени будет числом четным, а  в любой натуральной степени – число нечетное. Получаем противоречие, которое и доказывает, что корень уравнения – число иррациональное. Обдумывая, ситуацию с показательным уравнением
в любой натуральной степени – число нечетное. Получаем противоречие, которое и доказывает, что корень уравнения – число иррациональное. Обдумывая, ситуацию с показательным уравнением  математики ввели в рассмотрение новый символ – логарифм. С помощью этого символа корень уравнения
математики ввели в рассмотрение новый символ – логарифм. С помощью этого символа корень уравнения  записали так:
записали так:  (читается : логарифм числа
(читается : логарифм числа  по основанию
по основанию 
Остановимся теперь на понятии логарифма числа. Очень часто приходится решать задачу: известно, что  необходимо найти показатель степени
необходимо найти показатель степени  т.е. решить задачу, обратную возведению числа в степень. При нахождении этого показателя степени
т.е. решить задачу, обратную возведению числа в степень. При нахождении этого показателя степени  и возникает понятие логарифма числа
и возникает понятие логарифма числа  по основанию
по основанию 

дается определение логарифма
Например
а) log 3 81 = 4, так как 34 = 81;
б) log 5 125 = 3, так как 53 = 125;
в) log 0,5 16 = -4, так как (0,5)-4 = 16;
г)  , так как
, так как  =
= =
=
Введение основного логарифмического тождества
Из определения логарифма следует основное логарифмическое тождество:
( где b >0, a > 0 иa ≠ 1)
Согласно тождеству:
=5; .
Рассмотрим  =8
=8
Обратите внимание на то, что  является корнем уравнения
является корнем уравнения  , а поэтому
, а поэтому  =8
=8
Таким образом и получается основное логарифмическое тождество

Это равенство является краткой символической записью определения логарифмов.
Решить примеры согласно тождеству:  ;
;
 =5;
=5; 

 .
.
Подчеркнем, что  и
и  одна и та же математическая модель
одна и та же математическая модель
Операцию нахождения логарифма числа называют ЛОГАРИФМИРОВАНИЕМ. Эта операция является обратной по отношению к возведению в степень с соответствующим основанием.
По определению соотношения y = ax и x = loga y при условии, что a > 0 и a ≠ 1, эквиваленты. Переход от первого равенства ко второму называется логарифмированием , а переход от второго к первому – потенцированием.
Например:
- логарифмируя равенство:
 ,получаем log 1/2
,получаем log 1/2
- потенцируя равенство:
 , log2 8 = 3, будем иметь 23 = 8
, log2 8 = 3, будем иметь 23 = 8
Сравните.
Основные свойства логарифмов
Эти свойства вытекают из определения логарифма и свойств показательной функции.
При любом a > 0 (a  1) и любых положительных x и y выполнены равенства:
1) и любых положительных x и y выполнены равенства:
- loga 1 = 0.
- loga a = 1.
- loga xy = loga x + loga y.
- loga = loga x - loga y.
- loga xp = p loga x
для любого действительного p.
Решить примеры устно. Найти x
 Ответ:
Ответ: 
 Ответ:
Ответ: 
 Ответ:
Ответ:
 Ответ:
Ответ: 
 Ответ:
Ответ:
Упростить выражения:
a) 
б)
в) 
Ответ. a)  ; б)
; б) ; в)
; в) 
5. Закрепление изученного материала
Найти логарифм по основанию a числа представленного в виде степени с основанием a

Упростите выражения, пользуясь основным логарифмическим тождеством.
Выполнить упражнения. Работа по индивидуальным карточкам.











Просмотр содержимого документа
«Логарифмы и их свойства»
Дата проведения:
Группа:
Тема: «Логарифмы и их свойства».
Цели и задачи урока:
Образовательная: рассмотреть понятие логарифма числа и свойства логарифмов;
овладеть знаниями и умениями использовать основное логарифмическое тождество, формулы перехода от одного основания к другому в процессе решения упражнений;
Развивающая: развивать мышление учащихся при выполнении упражнений;
научить учащихся определять логарифм числа и его свойства;
Воспитательная: воспитать интерес к уроку.
Тип урока: усвоение новых знаний.
Методическое обеспечение: учебники, индивидуальные карточки.
Литература: учебник математики 10 кл. Колмогоров А.Н.
Ход занятия
1. Организационный момент
Перед началом урока преподаватель проводит проверку подготовленности кабинета к занятию.
Сообщается тема и цель урока.
2. Актуализация знаний
В кратком вступительном слове преподаватель акцентирует внимание студентов о важной
роли логарифмов в курсе математики.
3. Повторение ранее изученного материала
Опрос
Преподаватель задает вопросы:
1) Что такое степень; что такое основание степени; что такое показатель степени.
2) Работа над основными свойствами степеней. Рассмотреть связь между показателями степеней в равенствах
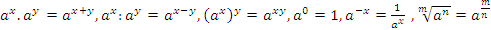
3) Решить устно примеры:
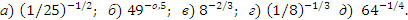
4. Изучение нового материала
План
1. Логарифм числа. Основные свойства логарифмов.
2. Основное логарифмическое тождество.
3. Формула перехода одного основания логарифмов к другому.
Преподаватель излагает новый учебный материал
Логарифм числа
Понятие логарифма числа связано с решением показательных уравнений.
Остановимся на решении двух показательных уравнений. Решение уравнения  не вызывает труда. Так как
не вызывает труда. Так как 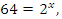 то данное уравнение примет вид
то данное уравнение примет вид  Поэтому уравнение имеет единственное решение
Поэтому уравнение имеет единственное решение 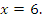
А теперь попробуем решить уравнение 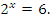 По теореме о корне это уравнение также имеет единственное решение. Однако, в отличие от предыдущего уравнения, это уравнение является иррациональным числом. Докажем, что корень данного уравнения является числом рациональным, т.е.
По теореме о корне это уравнение также имеет единственное решение. Однако, в отличие от предыдущего уравнения, это уравнение является иррациональным числом. Докажем, что корень данного уравнения является числом рациональным, т.е.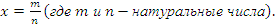 Тогда выполняется равенство
Тогда выполняется равенство  или
или  Но
Но  в любой натуральной степени будет числом четным, а
в любой натуральной степени будет числом четным, а 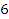 в любой натуральной степени – число нечетное. Получаем противоречие, которое и доказывает, что корень уравнения – число иррациональное. Обдумывая, ситуацию с показательным уравнением
в любой натуральной степени – число нечетное. Получаем противоречие, которое и доказывает, что корень уравнения – число иррациональное. Обдумывая, ситуацию с показательным уравнением  математики ввели в рассмотрение новый символ – логарифм. С помощью этого символа корень уравнения
математики ввели в рассмотрение новый символ – логарифм. С помощью этого символа корень уравнения  записали так:
записали так:  (читается : логарифм числа
(читается : логарифм числа 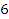 по основанию
по основанию 
Остановимся теперь на понятии логарифма числа. Очень часто приходится решать задачу: известно, что  необходимо найти показатель степени
необходимо найти показатель степени 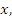 т.е. решить задачу, обратную возведению числа в степень. При нахождении этого показателя степени
т.е. решить задачу, обратную возведению числа в степень. При нахождении этого показателя степени 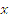 и возникает понятие логарифма числа
и возникает понятие логарифма числа  по основанию
по основанию 

дается определение логарифма
Например
а) log 3 81 = 4, так как 34 = 81;
б) log 5 125 = 3, так как 53 = 125;
в) log 0,5 16 = -4, так как (0,5)-4 = 16;
г)  , так как
, так как 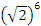 =
= =
=
Введение основного логарифмического тождества
Из определения логарифма следует основное логарифмическое тождество:
( где b 0, a 0 иa ≠ 1)
Согласно тождеству:
=5; .
Рассмотрим  =8
=8
Обратите внимание на то, что 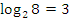 является корнем уравнения
является корнем уравнения  , а поэтому
, а поэтому  =8
=8
Таким образом и получается основное логарифмическое тождество

Это равенство является краткой символической записью определения логарифмов.
Решить примеры согласно тождеству: 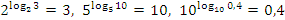 ;
;
 =5;
=5; 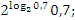
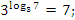
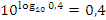 .
.
Подчеркнем, что  и
и  одна и та же математическая модель
одна и та же математическая модель
Операцию нахождения логарифма числа называют ЛОГАРИФМИРОВАНИЕМ. Эта операция является обратной по отношению к возведению в степень с соответствующим основанием.
По определению соотношения y = ax и x = loga y при условии, что a 0 и a ≠ 1, эквиваленты. Переход от первого равенства ко второму называется логарифмированием , а переход от второго к первому – потенцированием.
Например:
логарифмируя равенство:  ,получаем log 1/2
,получаем log 1/2
потенцируя равенство:  , log2 8 = 3, будем иметь 23 = 8
, log2 8 = 3, будем иметь 23 = 8
Сравните.
Основные свойства логарифмов
Эти свойства вытекают из определения логарифма и свойств показательной функции.
При любом a 0 (a 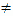 1) и любых положительных x и y выполнены равенства:
1) и любых положительных x и y выполнены равенства:
для любого действительного p.
Решить примеры устно. Найти x
 Ответ:
Ответ: 
 Ответ:
Ответ: 
 Ответ:
Ответ:
 Ответ:
Ответ: 
 Ответ:
Ответ:
Упростить выражения:
a) 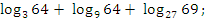
б)
в) 
Ответ. a) 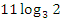 ; б)
; б) ; в)
; в) 
5. Закрепление изученного материала
Найти логарифм по основанию a числа представленного в виде степени с основанием a

Упростите выражения, пользуясь основным логарифмическим тождеством.
Выполнить упражнения. Работа по индивидуальным карточкам.





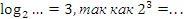
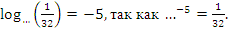
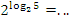

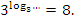
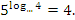


6. Подведение итогов, домашнее задание








 не вызывает труда. Так как
не вызывает труда. Так как  то данное уравнение примет вид
то данное уравнение примет вид  Поэтому уравнение имеет единственное решение
Поэтому уравнение имеет единственное решение 
 По теореме о корне это уравнение также имеет единственное решение. Однако, в отличие от предыдущего уравнения, это уравнение является иррациональным числом. Докажем, что корень данного уравнения является числом рациональным, т.е.
По теореме о корне это уравнение также имеет единственное решение. Однако, в отличие от предыдущего уравнения, это уравнение является иррациональным числом. Докажем, что корень данного уравнения является числом рациональным, т.е. Тогда выполняется равенство
Тогда выполняется равенство  или
или  Но
Но  в любой натуральной степени будет числом четным, а
в любой натуральной степени будет числом четным, а  в любой натуральной степени – число нечетное. Получаем противоречие, которое и доказывает, что корень уравнения – число иррациональное. Обдумывая, ситуацию с показательным уравнением
в любой натуральной степени – число нечетное. Получаем противоречие, которое и доказывает, что корень уравнения – число иррациональное. Обдумывая, ситуацию с показательным уравнением  математики ввели в рассмотрение новый символ – логарифм. С помощью этого символа корень уравнения
математики ввели в рассмотрение новый символ – логарифм. С помощью этого символа корень уравнения  (читается : логарифм числа
(читается : логарифм числа 
 необходимо найти показатель степени
необходимо найти показатель степени  т.е. решить задачу, обратную возведению числа в степень. При нахождении этого показателя степени
т.е. решить задачу, обратную возведению числа в степень. При нахождении этого показателя степени  и возникает понятие логарифма числа
и возникает понятие логарифма числа  по основанию
по основанию 

 , так как
, так как  =
= =
=
 =8
=8 является корнем уравнения
является корнем уравнения  , а поэтому
, а поэтому 
 ;
; =5;
=5; 

 .
. и
и  одна и та же математическая модель
одна и та же математическая модель ,получаем log 1/2
,получаем log 1/2 , log2 8 = 3, будем иметь 23 = 8
, log2 8 = 3, будем иметь 23 = 8 1) и любых положительных x и y выполнены равенства:
1) и любых положительных x и y выполнены равенства: Ответ:
Ответ: 
 Ответ:
Ответ: 
 Ответ:
Ответ:
 Ответ:
Ответ: 
 Ответ:
Ответ:



 ; б)
; б) ; в)
; в) 























