В данной разработке имеются карточки задания для самостоятельной работы, для устной работы, задания к зачету обязательный и повышенный уровень.
Просмотр содержимого документа
«Практический материал к ОГЭ по математике. "Уравнения"»
УРАВНЕНИЯ. ПРАКТИЧЕСКИЙ МАТЕРИАЛ
К ОГЭ ПО МАТЕМАТИКЕ.
КЛАСС
Содержание.
Уравнения. Карточки-задания (обязательный уровень).
Задания для устной работы.
Алгоритмы решения уравнений (обязательный уровень).
Ответы (обязательный уровень).
Задания к уроку практикуму. Алгоритмы решения уравнений (повышенный уровень).
Задания к зачёту (повышенный уровень).
Ответы (повышенный уровень).
Приложение. Таблицы контроля.
Уравнения. Карточки-задания. Обязательный уровень.
| К. № 1 ОУ Решите уравнения:  + + 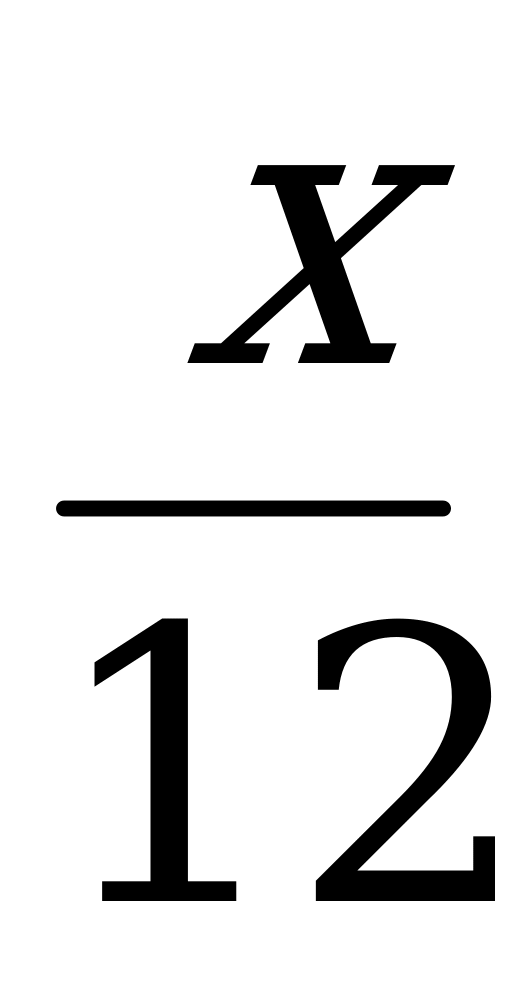 = =  2 − 3(x + 2) = 5 − 2x 10x2 + 5x = 0 4 − 36x2 = 0 2x2 + 3x − 5 = 0 12 − x2 = 11 (10x − 4)(3x + 2) = 0  = = 
| К. № 2 ОУ Решите уравнения:  + +  = =  3 − 5(x + 1) = 6 − 4x x2 − 10x = 0 2x2 − 10 = 0 2x2 + 3x − 2 = 0 x2 + 3 = 3 − x (3x + 1)(6 − 4x) = 0  = = 
|
| К. № 3 ОУ Решите уравнения:  + +  = 4 = 4 0,2 − 2(x + 1) = 0,4x x2 + 6x = 0 2x2 − 8 = 0 3x2 + 2x − 5 = 0 3x2 + 9 = 12x − x2 (5x − 4)(x + 8) = 0 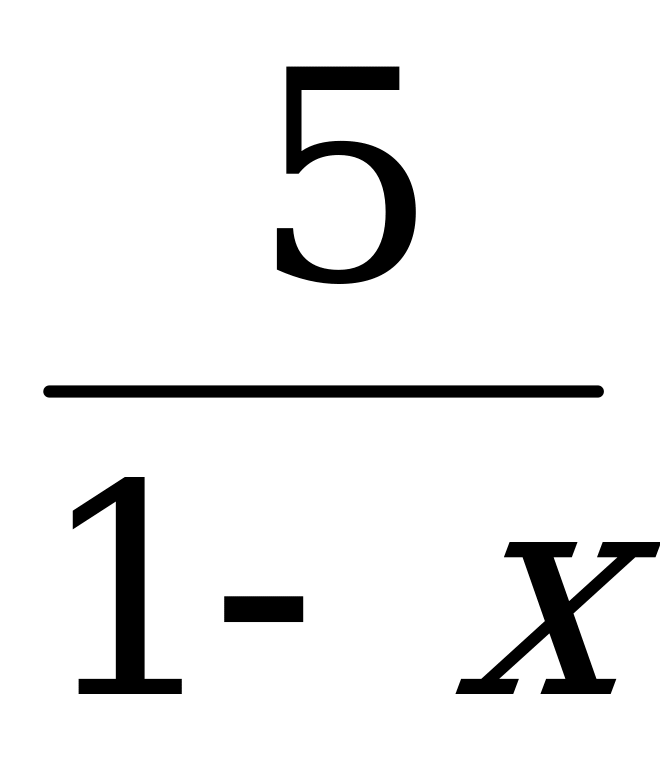 = = 
| К. № 4 ОУ Решите уравнения:  = =  0,4x = 0,4 − 2(x + 2) 4x2 + 20x = 0 3x2 − 75 = 0 9x2 − 6x + 1 = 0 5x2 + 1 = 6x − 4x2 (6x + 3)(9 − x) = 0  = = 
|
| К. № 5 ОУ Решите уравнения:  − −  = −3 = −3 4x − 5,5 = 5x − 3(2x − 1,5) 3x2 − 12x = 0 3x2 − 15 = 0 5x2 − 3x − 2 = 0 x(x + 2) = 3 (x + 5)(2x −  ) = 0 ) = 0  = = 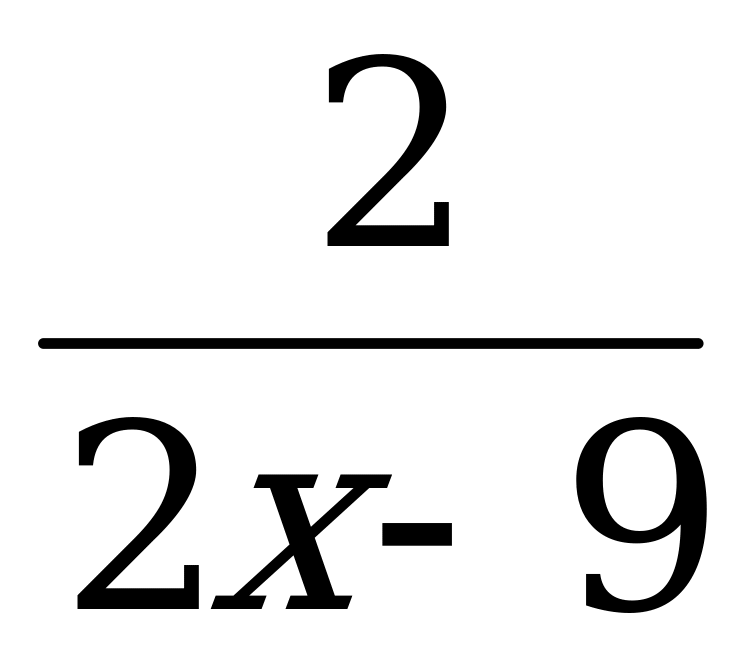
| К. № ОУ Решите уравнения:  − −  = − 1 = − 1 4 − 5(3x + 2,5) = 3x + 9,5 2x2 + x = 0 4x2 − 12 = 0 6x2 + x − 1 = 0 x(x + 3) = 4 (x − 1)(5x + 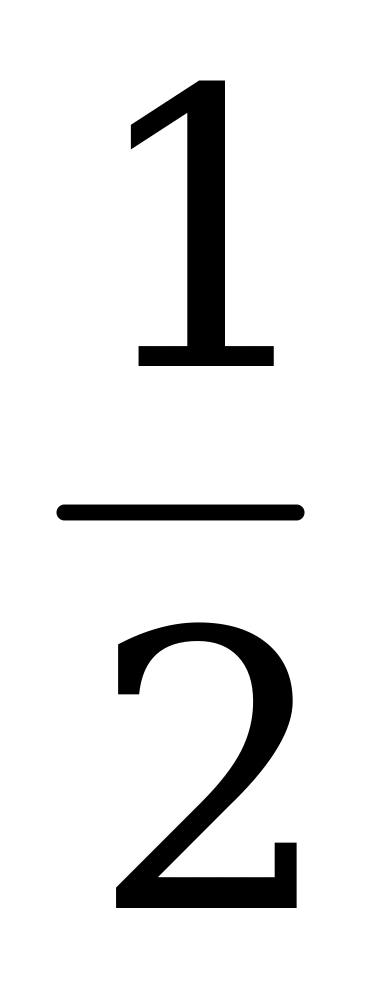 ) = 0 ) = 0  = = 
|
| К. № 7 ОУ Решите уравнения:  = =  5(2 + 1,5x) − 0,5x = 24 4x2 − x = 0 2x2 − 32 = 0 5x2 − 8x + 3 = 0 x(2x + 1) = 3x + 4 6(10 − x)(3x + 4) = 0  = 3 = 3
| К. № 8 ОУ Решите уравнения:  − −  = 3 = 3 3(0,5x − 4) + 8,5x = 18 25 − 100x2 = 0 3x2 − 27 = 0 7x2 + 9x + 2 = 0 x2 + 2x = 16x − 49 2(5x − 7)(1 + x) = 0  = = 
|
Задания для устной работы.
1. Решите неполное квадратное уравнение:
| 1)  | 6)  | 11)  | 16)  |
| 2)  | 7)  | 12)  | 17)  |
| 3) 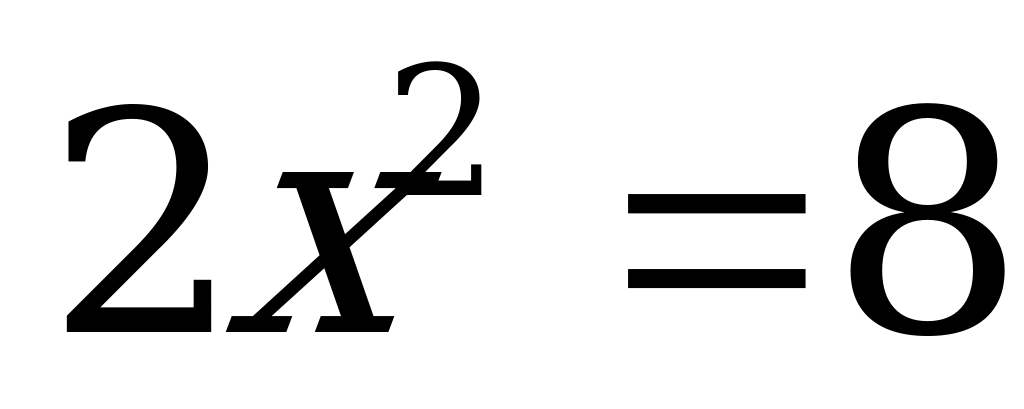 | 8) 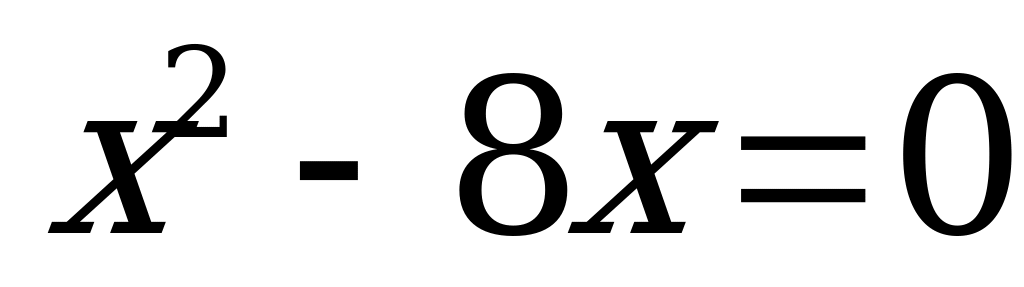 | 13)  | 18)  |
| 4)  | 9)  | 14)  | 19)  |
| 5)  | 10)  | 15)  | 20)  |
2. Решите квадратное уравнение, используя теорему Виета:

| 1)  | 6)  | 11)  | 16)  |
| 2) 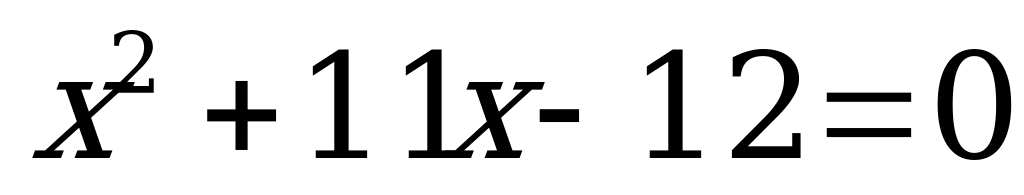 | 7)  | 12)  | 17)  |
| 3)  | 8)  | 13)  | 18)  |
| 4)  | 9)  | 14)  | 19)  |
| 5)  | 10)  | 15)  | 20)  |
3. Решите квадратное уравнение, используя формулу 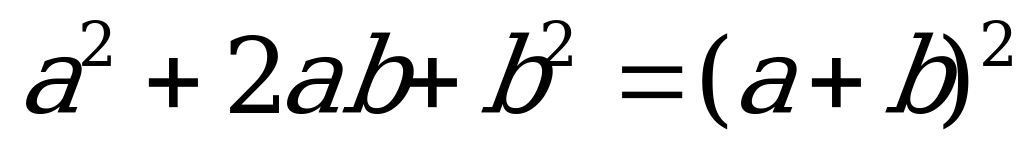 :
:
| 1)  | 6)  | 11)  | 16) 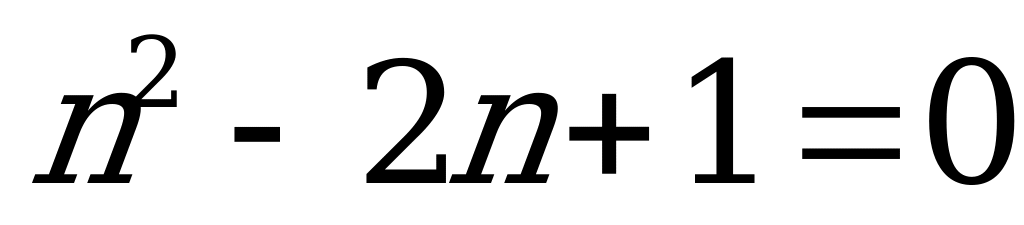 |
| 2)  | 7)  | 12) 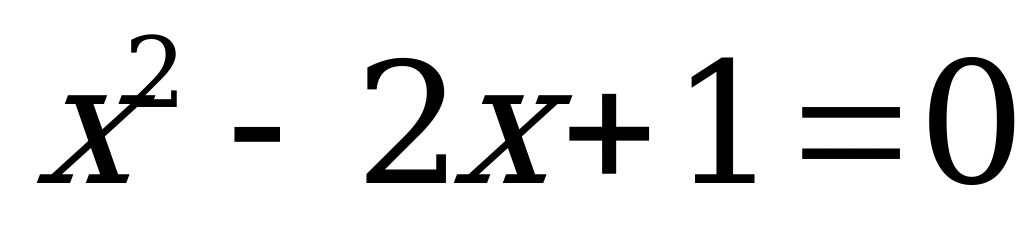 | 17)  |
| 3)  | 8)  | 13)  | 18)  |
| 4)  | 9)  | 14)  | 19)  |
| 5)  | 10)  | 15) 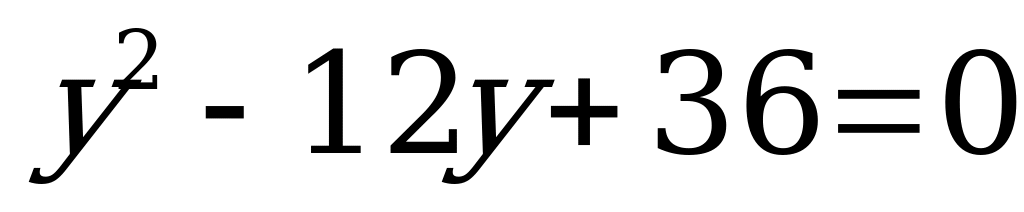 | 20)  |
4. Найдите дискриминант квадратного уравнения по формуле  :
:
| 1)  | 6) 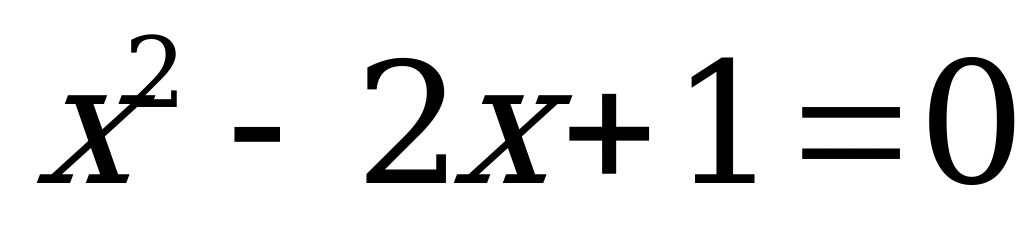 | 11)  | 16)  |
| 2)  | 7)  | 12) 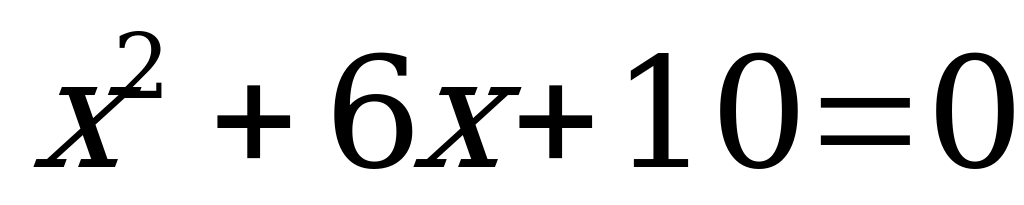 | 17)  |
| 3)  | 8)  | 13)  | 18)  |
| 4)  | 9) 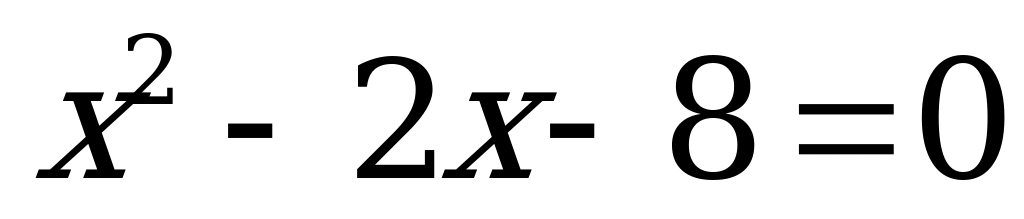 | 14)  | 19)  |
| 5)  | 10)  | 15)  | 20)  |
 5. Сколько корней имеет квадратное уравнение, если
5. Сколько корней имеет квадратное уравнение, если  равно:
равно:
| 1)  | 6)  | 11)  | 16)  |
| 2)  | 7)  | 12)  | 17)  |
| 3)  | 8)  | 13)  | 18)  |
| 4)  | 9)  | 14)  | 19)  |
| 5)  | 10)  | 15)  | 20) 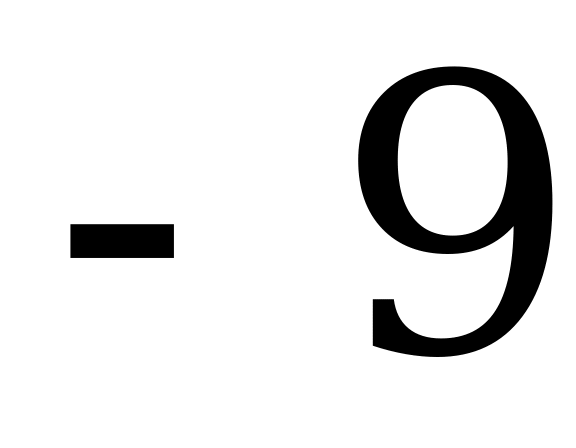 |
6. Решите квадратное уравнение:
| 1)  | 6) 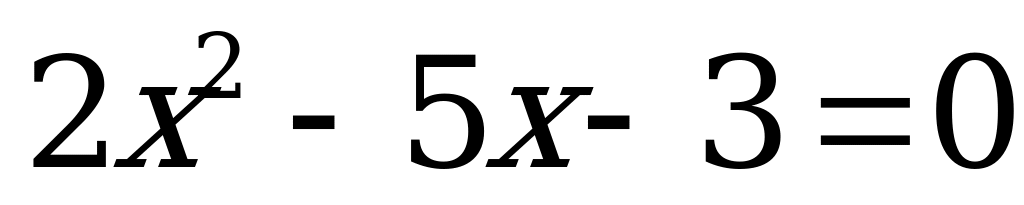 | 11)  | 16)  |
|
| 2)  | 7)  | 12)  | 17)  |
|
| 3)  | 8)  | 13)  | 18)  |
|
| 4)  | 9)  | 14)  | 19)  |
|
| 5)  | 10)  | 15)  | 20)  |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 Уравнения ОУ. Алгоритмы решения уравнений.
Уравнения ОУ. Алгоритмы решения уравнений.
Ответы. Уравнения. Обязательный уровень.
|
| К.№ 1 | К.№ 2 | К.№ 3 | К.№ 4 | К.№ 5 | К.№ 6 | К.№ 7 | К.№ 8 |
| 1 | 9 | 4 | 5,4 | -11 | 10 | 12 | 4 | 16 |
| 2 | -9 | -8 | -0,75 | -1,5 | 2 | -1 | 2 | 3 |
| 3 | -0,5; 0 | 0; 10 | -6; 0 | -5; 0 | 0; 4 | -0,5; 0 | 0; 025 | 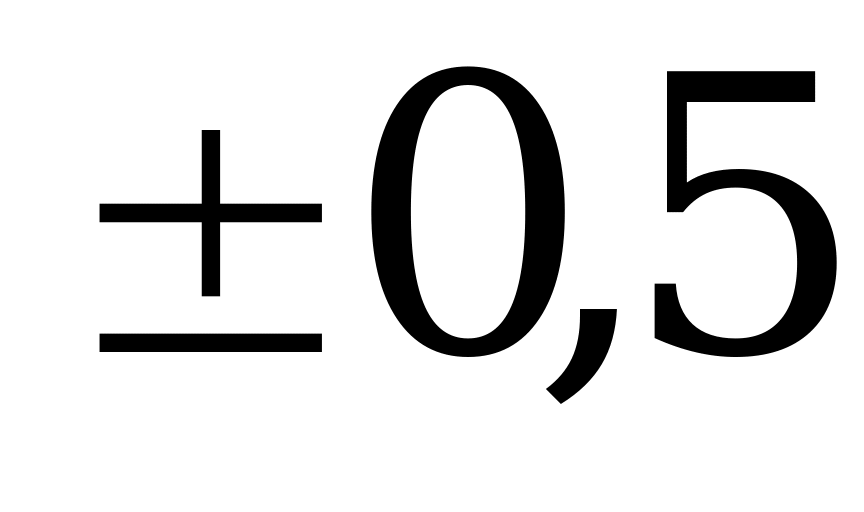
|
| 4 | 
| 
| 
| 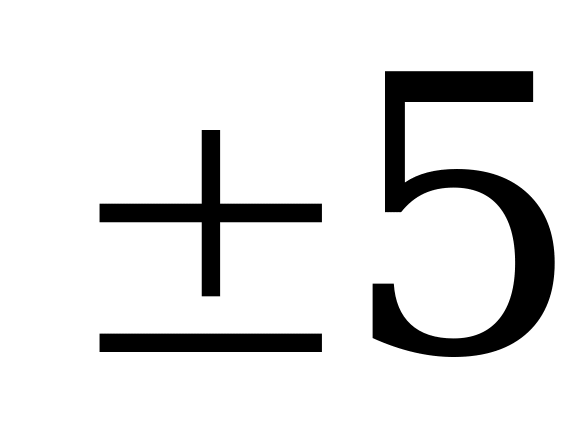
| 
| 
| 
| 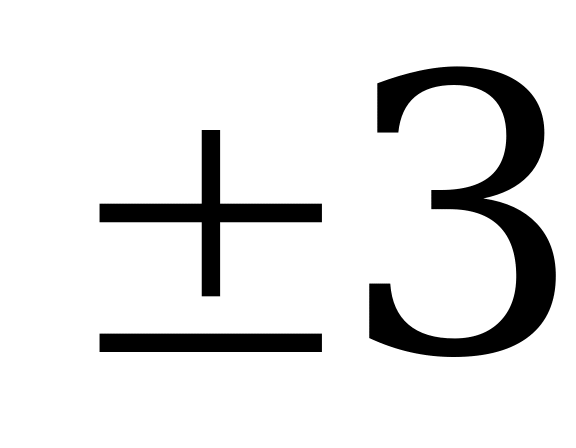
|
| 5 | -2,5; 1 | -2; 0,5 |  ; 1 ; 1
| 
| -0,4; 1 | 
| 
| 
|
| 6 | 
| -1; 0 | 1,5 | 
| -3; 1 | -4; 1 | -1; 2 | -1; 1,4 |
| 7 | 
| 
| -8; 0,8 | -0,5; 9 | -5; | -0.1; 1 | 10;  | -1; 1,4 |
| 8 | 4,6 | -0,2 | 26 | -6 | 3,75 | -2,6 | 3,75 | 2,6 |
Уравнения. Практикум. Задания повышенного уровня.
Уравнения. Повышенный уровень. Задания к зачёту.
| Задания. Решите уравнения: |
| 1.Биквадратные уравненния |
| 1) ; 2) ; 2)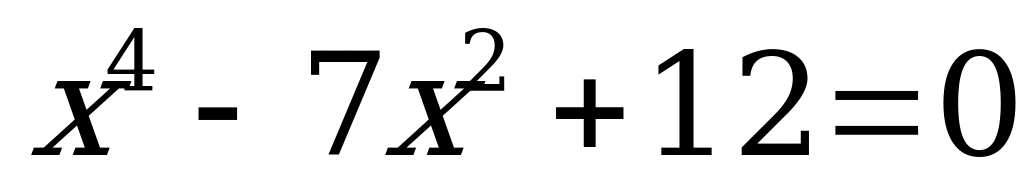 ; ; 3) : 4) : 4) . . |
| 2.Метод разложения на множители |
| 1)  ; 2) ; 2)  ; ; 3) 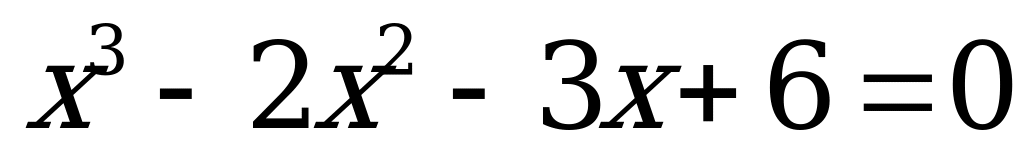 ; 4) ; 4)  |
| 3.Метод замены переменной |
| 1) ; 2) ; 2) 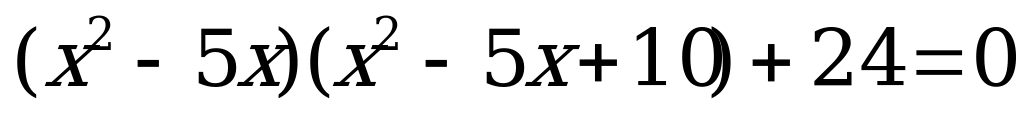 . . 3)  ; 4) ; 4)  |
| 4. Дробные рациональные уравнения |
| 1)  ; 2) ; 2)  ; ; 3)  ; 4) ; 4)  . .
|
| *5. Дробные рациональные уравнения |
| 1)  ; 2) ; 2)  ; ; 3)  ; 4) ; 4)  . . |
| * 6.Метод замены переменной |
| 1)  ; 2) ; 2)  ; ; 3) ; 4) ; 4)  . . |
| **7 Уравнения с параметром |
| 1) При каких значениях а корни уравнения: x2 – 2ax + (a + 1)(a – 1) = 0 принадлежат промежутку [− 5; 5]? 2) При каких значениях p корни уравнения: x2 – 2(p + 1)x + p(p + 2) = 0 принадлежат промежутку [− 1; 3]? 3) При каких значениях b уравнение x2 + 2(b + 1)x + 9 = 0 имеет два различных положительных корня? 4) При каких значениях k уравнение x2 – 4x + (2 – k)(2 + k) = 0 имеет корни разных знаков? |
| **Уравнения |
| 1)Не вычисляя корней x1 и x2 уравнения x2 − 7x − 21 = 0, найдите значение выражения: x12 + x22. 2) x1 = −3 является корнем уравнения 5x2 + 12x + q = 0. Найдите x2, q. 3) Сумма квадратов корней уравнения x2 + px − 3 = 0 равна 10. Найдите значение числа p. 4)Не вычисляя корней x1, x2 уравнения x2 − 7x + 12 = 0, найдите значение выражения: x12 + x22. Указание: 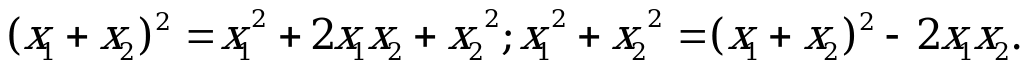   прив.ур. или прив.ур. или  ). ). |
Уравнения. Повышенный уровень. Ответы
.
Приложение.
Контроль знаний.
Уравнения Обязательный уровень.
| № п/п
| Фамилия имя | № зад.
№ К. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Контроль знаний.
Уравнения Повышенный уровень.
| № п/п
| Фамилия имя | № зад.
№ К. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
















