Презентация "Без знания дробей..."

« Без знания дробей никто не может признаваться знающим арифметику!..» Цицерон

Ученика 6 «А» класса МБОУ СОШ № 43

Терёхина Михаила

Учитель: Гончарова Светлана Алексеевна

2019 год

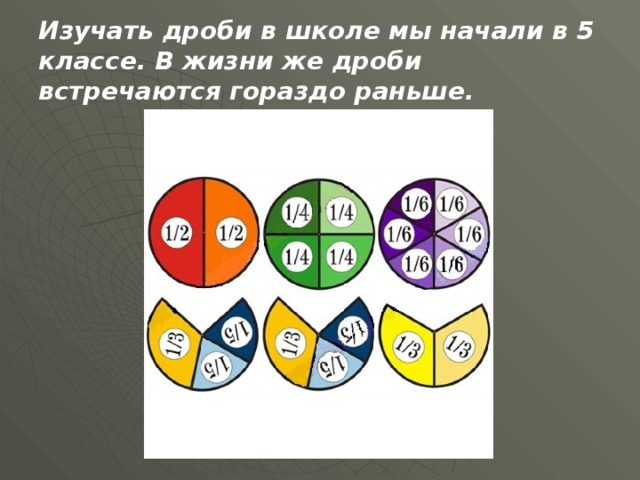
Изучать дроби в школе мы начали в 5 классе. В жизни же дроби встречаются гораздо раньше.

Цель исследования: изучить историю возникновения и практическую значимость дробей в жизни людей.

Задачи:

• Собрать материалы и изучить литературу по данной теме;
• Выяснить особенности возникновения дробей у разных народов в разные времена;

3. Проследить, как поменялась запись дроби на протяжении нескольких веков;

4. Убедиться в важности дробей.

Объект исследования: дроби

Гипотеза: Дроби необходимы в практической жизни человека. Без дробей не могла бы развиваться математика.

Методы исследования:

1. Поиск информации о дробях в различных источниках: интернете, художественной литературе, учебниках.

2. Анализ, сравнение, обобщение и систематизация информации.

О причинах возникновения дробей.

• Счет – самое древнее математическое действие.
• Необходимость в дробных числах возникла у человека на весьма ранней стадии развития.

• Как поделить добычу между участниками охоты, когда число животных оказывалось не кратным числу охотников?

•   Наряду с необходимостью считать предметы появилась потребность измерять длину, площадь, объём, время и другие величины.

• Результат измерений не всегда удаётся выразить натуральным числом, приходится учитывать и части употребляемой меры.

Что такое дробь?

• Само слово "дробь" происходит от латинского "fractio", что значит «ломать», «раздроблять».

С древних времен в этом смысле мало что изменилось. Современное определение звучит следующим образом: дробь — это часть или сумма частей единицы.

Учение о дробях издавна считалось самым трудным разделом математики. Кто знал дроби, был в почете.

• «Человек подобен дроби: числитель - это он сам, а знаменатель то, что он о себе думает. Чем больше знаменатель, тем меньше дробь». Л.Н. Толстой

Система записи дробей, правила действий с ними заметно различались как у разных народов, так и в разные времена у одного и того же народа.

Впервые оперировать дробями начали на территории Египта и Вавилона. Подход математиков двух государств имел значительные отличия. Однако начало было положено одинаково. Первой дробью стала половина или 1/2. Дальше возникла четверть, треть и так далее.

ЕГИПЕТСКИЕ ДРОБИ

Египетские дроби представляют собой сумму нескольких слагаемых вида 1/n.

Числитель — всегда единица, а знаменатель — натуральное число.

При расчетах все доли старались записывать в виде таких сумм (например, 1/2 + 1/4 + 1/8). Отдельными обозначениями обладали только дроби 2/3 и 3/4, остальные разбивались на слагаемые.

Существовали специальные таблицы, в которых доли числа представлялись в виде суммы.

Египтяне умели складывать, делить и умножать доли числа. Дроби в долине Нила записывались с помощью иероглифов.

МАТЕМАТИКА ВАВИЛОНСКОГО ЦАРСТВА

Система счисления в Вавилоне была шестидесятеричной. Каждый новый разряд отличался от предыдущего на 60. Такая система сохранилась в современном мире для обозначения времени и величин углов.

Дроби также были шестидесятеричными. Для записи использовали специальные значки. Как и в Египте, примеры с дробями содержали отдельные символы для обозначения 1/2, 1/3 и 2/3.

Вавилонская система не исчезла вместе с государством. Дробями, написанными в 60-тиричной системе, пользовались античные и арабские астрономы и математики.

ДРЕВНЯЯ ГРЕЦИЯ

• Греки свободно оперировали всеми арифметическими действиями с дробями, но числами их не признавали. Греческие ученые считали, что математика должна заниматься только целыми числами. Возиться с дробями они предоставляли купцам, ремесленникам, а также астрономам, землемерам, механикам и другому «черному люду».
• «Если ты захочешь делить единицу, математики высмеют тебя и не позволят это делать»,- писал основатель афинской академии Платон.

Но не все древнегреческие математики соглашались с Платоном.

• Пифагор с учениками понимали дроби как отношения или пропорции, а единицу считали также неделимой. построил общую теорию дробей, научился проводить все четыре арифметические операции, а также сравнение дробей путем приведения их к общему знаменателю.

Священная римская империя

• Римская система дробей была связана с мерой веса, называемой «асс». Она делилась на 12 долей. 1/12 асса называлась унцией. Для обозначения дробей существовало 18 названий.
• Например,

семис — половина асса; секстанте — шестая доля асса; семиунция — пол-унции или 1/24 асса.

Неудобство такой системы заключалось в невозможности представить число в виде дроби со знаменателем 10 или 100.

Древняя Индия

• Индийцы широко употребляли “обыкновенные” дроби. Наше обозначение обыкновенных дробей при помощи числителя и знаменателя было принято в Индии в VIII в.до н.э., однако

без дробной черты. Дробная черта стала применяться лишь в XIII в.

• Широко известны математики Древней Индии Ариабхатта (V в.), Брахмагупта (VII в.), изложивший правила действий с дробями, мало отличавшиеся от наших, и Бхаскара (XII в.). Последний написал книгу под названием “Лилавати”, т. е. “Прекрасная” (наука арифметика).
• Индийские ученые нередко излагали арифметические задачи в стихах.

Дроби на Руси

На Руси первым математиком, изложившим деление целого на части, стал новгородский монах Кирик.

Само слово «дробь» появилось на Руси в VIII веке. Для названия дробей наши предки использовали специальные слова.

1/2 - половина, полтина

1/3 – треть

1/4 – четь

1/6 – полтреть

1/8 - полчеть

1/12 –полполтреть

1/16 - полполчеть

1/24 – полполполтреть (малая треть)

1/32 – полполполчеть (малая четь)

1/5 – пятина

1/7 - седьмина

1/10 – десятина.

Магницкий Леонтий Филиппович.

Полная теория дробей, мало чем отличающаяся от современной, была изложена Л.Ф.Магницким в первом учебнике по арифметике, написанном в 1701 году. Магницкий приводит операции с «ломанными» числами, разные их обозначения.

Современная запись дроби

Знаете ли вы, что привычных для нас дробей, которые мы используем сегодня, не существовало в Европе вплоть до XVII века!

В Античности дроби уже писали знакомым нам образом: одно число над другим. Однако было одно существенное отличие. Числитель располагался под знаменателем . Впервые так писать дроби начали в древней Индии.

Современный нам способ стали использовать арабы. Первым дробную черту стал применять арабский ученый Ал-Халар.

Но никто из названных народов не применял горизонтальную черту для разделения числителя и знаменателя. Впервые она появляется в трудах итальянского математика Леонардо Пизанского , более известного как Фибоначчи, в 1202 году.

• Исторические
• задачи
• с обыкновенными
• дробями

• Древнеиндийская
• задача о цветах и пчелах

• Задача из "Арифметики"
• Леонтия Филипповича
• Магницкого

• Древнегреческая задача
• о статуе Миневры
• (богини мудрости,
• покровительнице наук,
• искусств и ремесел).

Древнегреческая задача о статуе Минервы

• Задача:

Я изваяние из злата, поэты то злато в дар принесли.  Хоризий принес половину сей жертвы. Фестия часть восьмую дала, десятую — Солон.  Часть двадцатая — жертва певца Фемисона. А девять — все завершивших талантов —  Обет, Аристоником данный. Сколько же злата поэты все вместе в дар принесли?

• Решение.

НОК (2,8,10,20) = НОК (8,20) = 40

• Ответ: 40.

Староиндийская задача с цветами и пчелами.

• “ Есть “кадамба” цветок, На один лепесток Пчелок пятая часть опустилась. Рядом тут же росла Вся в цвету сименгда И на ней третья часть поместилась. Разность их ты найди, Ее трижды сложи И тех пчел на Кутай посади. Лишь одна не нашла Себе места нигде Все летала то взад, то вперед и везде Ароматом цветов наслаждаясь. Назови теперь мне, Подсчитавши в уме, Сколько пчелок всего здесь собралось”.
• Решение.

•   Ответ: 15.

Задача из "Арифметики" Леонтия Филипповича Магницкого. Эта задача трехвековой давности.

Один человек выпьет бочонок за 14 дней, а с женой выпьет тот же бочонок за 10 дней. За сколько дней жена его отдельно выпьет этот бочонок?

• Решение 1 способом.

Весь бочонок принят за - 1.

1)1:14=бочонка пьёт один человек в день.

1:10=бочонка пьёт муж и жена в день.

2) пьёт жена в день.

3)1:дней понадобится жене чтобы выпить бочонок.

Ответ:35 дней понадобится жене чтобы выпить бочонок.

• Решение 2 способом.

За 140 дней человек выпьет 10 бочонков кваса, а вдвоем с женой за 140 дней они выпьют 14 бочонков кваса. Значит, за 140 дней жена выпьет 14-10 = 4 бочонка кваса, а тогда один бочонок она выпьет за 140:4 = 35 дней.

Ответ: за 35 дней выпьет жена.

Где еще, кроме математики, мы встречаемся со словом «дробь»?

• Мелкие свинцовые шарики для стрельбы из охотничьего ружья - дробь.
• Частые, прерывистые звуки - барабанная дробь.
• На флоте, команда «дробь!» — прекращение огня.
• Нумерация домов. Номер через дробь ставят у домов, пронумерованных по двум пересекающимся улицам.
• Дробь в танце. Русский народный танец невозможно представить без дробей и бега.
• Выбивать дробь зубами – стучать зубами (дрожа от холода, испуга).
• В моде присутствовали дроби. Всегда актуален фасон рукава три четверти, укороченные брюки 7/8

С дробями мы встречаемся на уроке географии

• Во времена существования СССР, Россия занимала одну шестую часть суши. Теперь Россия занимает одну девятую часть суши.
• Участки земной поверхности изображаются на карте в уменьшенном виде, для этого используется понятие масштаба: отношение длины отрезка на карте к длине соответствующего отрезка на местности.

Дроби в музыке.

• Я учусь в музыкальной школе, и я знаю, длинная нота –целая – делится на половинки(вдвое короче), четверти, шестнадцатые и тридцать вторые; что 6/8 – это три четверти, и что в одной половине восемь шестнадцатых.
• Таким образом, ритмичный рисунок любого музыкального произведения, каким бы он сложным ни был, определяется обыкновенными дробями.

ВЫВОДЫ:

• Всегда учение о дробях вырастало из практических наблюдений и благодаря насущным проблемам.
• Особенности применения дробей и математических операций с ними зависели от системы счисления в государстве и от общего уровня развития математики.
• Учение о дробях – самый сложный раздел математики. Немцы говорят про человека, попавшего в затруднительное положение, что он «попал в дроби».
• Сегодня нет такой области знаний, где в той или иной степени не использовались бы математические понятия о дробях.

СПАСИБО ЗА ВНИМАНИЕ

Источники.

Личные наблюдения.

Литература:

1. М.Я.Выгодский “Арифметика и алгебра в Древнем мире”(М. Наука,1967г)

2. Г.И.Глейзер “История математики в школе”(М. Просвещение,1964г)

3. И.Я.Депман “История арифметики” (М. Просвящение, 1959г)

4. И. Депман «Рассказы о математике» , издательство «Детгиз», г. Ленинград, 1954 год.

5. Л.В. Гончарова «Предметные недели в школе. МАТЕМАТИКА» , издательство «Учитель», г. Волгоград, 2000 год.

6. С.М. Никольский «Арифметика» , издательство «Наука», г. Москва, 1988 год.

Интернет источники:

• http://fb.ru/article/236507/drobi-istoriya-drobey-istoriya-vozniknoveniya-obyiknovennyih-drobey
• https://pandia.ru/text/78/053/30631.php
• http://book-science.ru/exact/maths/proishozhdenie-drobej.html
• https://cyberpedia.su/3x6de.html
• https://school-science.ru/3/7/33498