Презентация по теме "Вероятность"

Классическое определение вероятности

Определение вероятности

Вероятностью события A называют отношение числа m благоприятствующих этому событию исходов к общему числу n всех равновозможных несовместимых событий, которые могут произойти в результате одного испытания или наблюдения:

m

Р =

n

Пусть k – количество бросков монеты, тогда количество всевозможных исходов: n = 2 k .

Пусть k – количество бросков кубика, тогда количество всевозможных исходов: n = 6 k .

Свойства вероятности

Свойство 1. Вероятность достоверного события равна единице: Р(А) = 1 .

Свойство 2. Вероятность невозможного события равна нулю: Р(А) = 0 .

Свойство 3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей: 0 ≤ Р(А) ≤ 1 .

В сборнике билетов по биологии всего 55 билетов, в 11 из них встречается вопрос по ботанике. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по ботанике.

285926

Решение:

Вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по ботанике, равна 11/55 =1/5 = 0,2.

Ответ: 0,2.

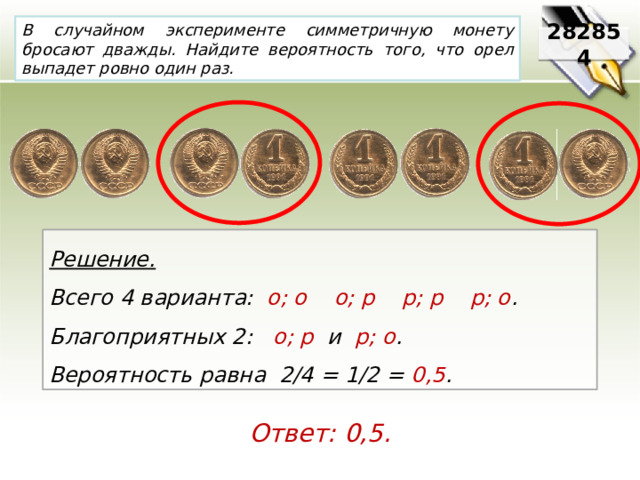
В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз.

282854

Решение.

Всего 4 варианта:   о; о    о; р    р; р    р; о .    

Благоприятных 2:   о; р  и р; о .  

Вероятность равна 2/4 = 1/2 = 0,5 .

Ответ: 0,5.

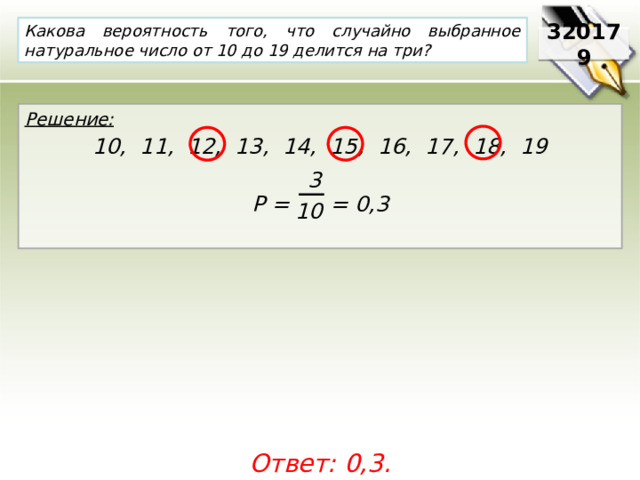
Какова вероятность того, что случайно выбранное натуральное число от 10 до 19 делится на три?

320179

Решение:

10, 11, 12, 13, 14, 15, 16, 17, 18, 19

Р = = 0,3

3

10

Ответ: 0,3.

Вася, Петя, Коля и Лёша бросили жребий – кому начинать игру. Найдите вероятность того, что начинать игру должен будет Петя.

320169

Решение:

Вероятность того, что игру должен будет начинать любой из мальчиков равна

1/4 = 0,25.

В том числе и для Пети.

Ответ: 0,25.

В чемпионате по гимнастике участвуют 20 спортсменок: 8 из России, 7 из США, остальные − из Китая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Китая.

282855

Решение.

Всего участвует 20 спортсменок,

из которых 20 – 8 – 7 = 5 спортсменок из Китая.

Вероятность того, что спортсменка, выступающая первой, окажется из Китая, равна 5/20 = 1/4 = 0,25.

Ответ: 0,25.

В среднем из 1000 садовых насосов, поступивших в продажу, 5 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.

282856

Решение:

1000 – 5 = 995 – насосов не подтекают.

Вероятность того, что один случайно выбранный для контроля насос не подтекает, равна

995/1000 = 0,995.

Ответ: 0,995.

Фабрика выпускает сумки. В среднем на 100 качественных сумок приходится восемь сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.

282857

Решение:

100 + 8 = 108 – сумок всего (качественных и со скрытыми дефектами).

Вероятность того, что купленная сумка окажется качественной, равна 100/108 = 0,(925) ≈ 0,93.

Ответ: 0,93.

В соревнованиях по толканию ядра участвуют 4 спортсмена из Финляндии, 7 спортсменов из Дании, 9 спортсменов из Швеции и 5 − из Норвегии. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, который выступает последним, окажется из Швеции.

282858

Решение:

Всего участвует 4 + 7 + 9 + 5 = 25 спортсменов. Вероятность того, что спортсмен, который выступает последним, окажется из Швеции, равна

9/25 = 36/100 = 0,36.

Ответ: 0,36.

Научная конференция проводится в 5 дней. Всего запланировано 75 докладов − первые три дня по 17 докладов, остальные распределены поровну между четвертым и пятым днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?

285922

Решение:

В последний день конференции запланировано

(75 – 17 × 3) : 2 = 12 докладов.

Вероятность того, что доклад профессора М. окажется запланированным на последний день конференции, равна 12/75 = 4/25 = 0,16.

Ответ: 0,16.

Конкурс исполнителей проводится в 5 дней. Всего заявлено 80 выступлений − по одному от каждой страны. В первый день 8 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьёвкой. Какова вероятность, что выступление представителя России состоится в третий день конкурса?

285923

Решение:

В третий день конкурса запланировано

(80 – 8) : 4 = 18 выступлений.

Вероятность того, что выступление представителя России состоится в третий день конкурса, равна

18/80 = 9/40 = 225/1000 = 0,225.

Ответ: 0,225.

На семинар приехали 3 ученых из Норвегии, 3 из России и 4 из Испании. Порядок докладов определяется жеребьёвкой. Найдите вероятность того, что восьмым окажется доклад ученого из России.

285924

Решение:

Всего участвует 3 + 3 + 4 = 10 ученых.

Вероятность того, что восьмым окажется доклад ученого из России, равна 3/10 = 0,3.

Ответ: 0,3.

Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 бадминтонистов, среди которых 10 участников из России, в том числе Руслан Орлов. Найдите вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России?

285925

Решение:

Нужно учесть, что Руслан Орлов должен играть с каким-либо бадминтонистом из России. И сам Руслан Орлов тоже из России.

Вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России, равна 9/25 = 36/100 = 0,36.

Ответ: 0,36.

В сборнике билетов по математике всего 25 билетов, в 10 из них встречается вопрос по неравенствам. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по неравенствам.

285927

Решение:

25 – 10 = 15 – билетов не содержат вопрос по неравенствам.

Вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по неравенствам, равна

15/25 = 3/5 = 0,6.

Ответ: 0,6.

На чемпионате по прыжкам в воду выступают 25 спортсменов, среди них 8 прыгунов из России и 9 прыгунов из Парагвая. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что шестым будет выступать прыгун из Парагвая.

285928

Решение:

Всего участвует 25 спортсменов.

Вероятность того, что шестым будет выступать прыгун из Парагвая, равна 9/25 = 36/100 = 0,36.

Ответ: 0,36.

Даша дважды бросает игральный кубик. В сумме у нее выпало 8 очков. Найдите вероятность того, что при первом броске выпало 2 очка.

Решение.

В сумме на двух кубиках должно выпасть 8 очков. Это возможно, если будут следующие комбинации:

2 и 6

6 и 2

3 и 5

5 и 3

4 и 4

Всего 5 вариантов. Подсчитаем количество исходов (вариантов), в которых при первом броске выпало 2 очка.

Такой вариант 1.

Найдем вероятность:   1/5 = 0,2.

Ответ: 0,2.

На клавиатуре телефона 10 цифр, от 0 до 9. Какова вероятность того, что случайно нажатая цифра будет чётной?

320178

Решение:

Количество четных цифр на клавиатуре равно 5:

0, 2, 4, 6, 8

всего же цифр на клавиатуре 10, тогда вероятность что случайно нажатая цифра будет чётной равна

5/10 = 0,5.

Ответ: 0,5.

Ковбой Джон попадает в муху на стене с вероятностью 0,9, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,2. На столе лежит 10 револьверов, из них только 4 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.

320183

Решение:

Вероятность того, что Джон промахнется, если схватит пристрелянный револьвер равна:

0,4 · (1 − 0,9) = 0,04

Вероятность того, что Джон промахнется, если схватит непристрелянный револьвер равна:

0,6 · (1 − 0,2) = 0,48

Эти события несовместны, вероятность их суммы равна сумме вероятностей этих событий:

0,04 + 0,48 = 0,52.

Ответ: 0,52.

В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что наступит исход ОР (в первый раз выпадает орёл, во второй – решка).

320185

Решение.

Всего 4 варианта:   о; о    о; р    р; р    р; о .    

Благоприятных 1:   о; р .  

Вероятность равна 1/4 = 0,25 .

Ответ: 0,25.

На олимпиаде в вузе участников рассаживают по трём аудиториям. В первых двух по 120 человек, оставшихся проводят в запасную аудиторию в другом корпусе. При подсчёте выяснилось, что всего было 250 участников. Найдите вероятность того, что случайно выбранный участник писал олимпиаду в запасной аудитории.

320191

Решение:

Всего в запасную аудиторию направили

250 − 120 − 120 = 10 человек.

Поэтому вероятность того, что случайно выбранный участник писал олимпиаду в запасной аудитории, равна

P = 10 : 250 = 0,04.

Ответ: 0,04.

В классе 26 человек, среди них два близнеца – Андрей и Сергей. Класс случайным образом делят на две группы по 13 человек в каждой. Найдите вероятность того, что Андрей и Сергей окажутся в одной группе.

320192

Решение:

Пусть один из близнецов находится в некоторой группе.

Вместе с ним в группе окажутся 12 человек из 25 оставшихся одноклассников.

Вероятность того, что второй близнец окажется среди этих 12 человек, равна

P = 12 : 25 = 0,48.

Ответ: 0,48.

В фирме такси в наличии 50 легковых автомобилей; 27 из них чёрные с жёлтыми надписями на бортах, остальные – жёлтые с чёрными надписями. Найдите вероятность того, что на случайный вызов приедет машина жёлтого цвета с чёрными надписями.

320193

Решение:

Машин желтого цвета с черными надписями 23, всего машин 50. Поэтому вероятность того, что на случайный вызов приедет машина желтого цвета с черными надписями, равна:

P = 23 : 50 = 0,46.

Ответ: 0,46.

Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали ходить. Найдите вероятность того, что часовая стрелка застыла, достигнув отметки 10, но не дойдя до отметки 1 час.

320209

Решение:

На циферблате между десятью часами и одним часом три часовых деления. Всего на циферблате 12 часовых делений.

Поэтому искомая вероятность равна:

Ответ: 0,25.

Используемые материалы

• ЕГЭ 2012. Математика. Задача В10. Теория вероятностей. Рабочая тетрадь / Под ред. А.Л. Семенова и И.В. Ященко.− М.: МЦНМО, 2012. − 48 с.

• ЕГЭ: 3000 задач с ответами по математике. Все задания группы В / под ред. А.Л. Семенова, И.В. Ященко. – 3-е изд., перераб. и доп. – М.: Издательство «Экзамен», 2012. – 543 с.

• http://mathege.ru/or/ege/Main.html − Материалы открытого банка заданий по математике 2013 года

• http://reshuege.ru/ − Сайт Дмитрия Гущина