Презентация "Возведение в квадрат и в куб суммы и разности двух выражений"

На большом листе бумаги изображена карта с изображением эмоциональных "островов": о. Радости, о. Грусти, о. Недоумения, о. Тревоги, о. Ожидания, о. Просветления, о. Воодушевления, о. Удовольствия, о. Наслаждения, Бермудский треугольник и др.

На карте островов зарисуйте остров в соответствующем районе карты, который отражает душевное, эмоционально-чувственное состояние в начале урока, в течении урока и в конце урока.

О-в Грусти

Бермудский треугольник

О-в Воодушевления

О-в Просветления

О-в.Удовольствия

О-в Тревоги

О-в Радости

О-в Ожидания

О-в Недоумения

О-в Неопределенности

О-в Наслаждения

Ведется на протяжении всего урока.

Фамилия, имя ученика_____________________________

Вид задания

Количество ошибок

ВОЗВЕДЕНИЕ В КВАДРАТ И В КУБ СУММЫ И РАЗНОСТИ ДВУХ ВЫРАЖЕНИЙ .

7 КЛАСС

« Дороги не те знания, которые откладываются в мозгу, как жир; дороги те, которые превращаются в умственные мышцы»

Герберт Спенсер

ЦЕЛЬ: 1) обобщить знания учащихся по данной теме;

2) закрепить умение применять формулы

3) воспитать у учащихся любознательность;

4) развивать познавательный интерес, логическое мышление;

5) развивать навыки коллективной работы учащихся с самостоятельным умением анализировать, выделять главное, обобщать и делать выводы.

ПРЕОБРАЗУЙТЕ В МНОГОЧЛЕН

х 2 + 2ху + у 2

a 3 + 3 a 2 b + 3ab 2 + b 3

4m 2 - 4mn + n 2

у 3 - 9у 2 х + 9ух 2 - 27х 3

4a 2 + 1 2 a + 9

9 – 6b + b 2

a 2 + 4a + 4

(х + у) 2 =

( a + b ) 3 =

( 2m - n ) 2 =

(у – 3х) 3 =

( 2a + 3 ) 2 =

( 3 - b ) 2 =

( a + 2 ) 2 =

МОЛОДЕЦ!!!

Е

В

Куб разности двух выражений

К

Квадрат разности двух выражений

Куб суммы двух выражений

Л

И

(a - b) 3 = a 3 - 3a 2 b + 3ab 2 - b 3

(a - b) 2 = a 2 - 2ab + b 2

Д

(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3

Древнегреческий математик, автор знаменитого трактата «Начала»

А знаете ли вы,

что древнегреческий философ Евклид ещё за три века д.н.э. умел возводить в квадрат сумму двух выражений, геометрический смысл формулы был приведен Эвклидом в «Началах»: « Если отрезок как-либо разбит на два отрезка, то площадь квадрата, построенного на всем отрезке, равна сумме площадей квадратов, построенных на каждом из двух отрезков, и удвоенной площади прямоугольника, сторонами которого служат эти два отрезка .»

• А как вы думаете, в какой формуле сокращённого умножения, заключается эта фраза:

ПРОВЕРКА ЗНАНИЙ ФОРМУЛ:

Преобразуйте в многочлен:

1) ( m + n ) 2 = m 2 + 2mn + n 2

2) (х - у) 2 = х 2 - 4ху 2 + у 2

3) (у + 3) 2 = у 2 + 6у - 9

4) (2 - а) 2 = 4 – 4а + а 2

5) (х + 2,5) 2 = х 2 + 5х + 6,25

Представьте в виде квадрата двучлена:

6) у 2 + 10у + 25 = (у + 5) 2

7) 4х 2 - 4ху + у 2 = (2х + у) 2 8) у 3 - 9у 2 х + 9ух 2 - 27х 3 = (у – 3х) 3

9) 64х 2 + 48х – 9 = (8х + 3) 2 10) 100у 2 - 140ху + 49х 2 = (10у – 7х) 2

ПРОВЕРЯЕМ:

Преобразуйте в многочлен:

1) ( m + n ) 2 = m 2 + 2mn + n 2 - верно

2) (х - у) 2 = х 2 - 4ху 2 + у 2 - не верно

3) (у + 3) 2 = у 2 + 6у - 9 - не верно

4) (2 - а) 2 = 4 – 4а + а 2 - верно

5) (х + 2,5) 2 = х 2 + 5х + 6,25 - верно

Представьте в виде квадрата двучлена:

6) у 2 + 10у + 25 = (у + 5) 2 - верно

7) 4х 2 - 4ху + у 2 = (2х + у) 2 - не верно 8) у 3 - 9у 2 х + 9ух 2 - 27х 3 = (у – 3х) 3 – не верно

9) 64х 2 + 48х – 9 = (8х + 3) 2 - не верно 10) 100у 2 - 140ху + 49х 2 = (10у – 7х) 2 - верно

ФИЗКУЛЬТМИНУТКА

• Потереть ладонью о ладонь. Закрыть глаза и положить на них ладони. Отдых 10 – 15 сек.
• Быстро поморгать глазами. Закрыть глаза. Отдых 10 – 15 сек.
• Открыть глаза.

САМОСТОЯТЕЛЬНО:

1 УРОВЕНЬ

2 УРОВЕНЬ

( х - у ) ² - у ² =

( 2a + 3b ) ² - 8b(2a + b)=

( a + d ) ² - a² =

(5 х - 3 у ) ² + 30 х у =

(3 х - 2 у ) ² =

(6 a + 2 b ) ² - 24 ab =

( 3 х – 2у) ² + 5х ( 4у - х ) =

( 2a + 3b ) ² =

(2 + a) 3 =

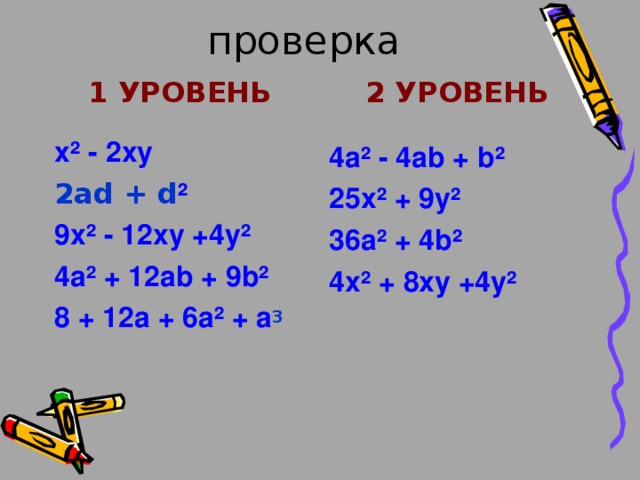
проверка

1 УРОВЕНЬ

2 УРОВЕНЬ

х ² - 2ху

2ad + d ²

9 х ² - 12ху +4у ²

4 a² + 12ab + 9b²

8 + 12a + 6a² + a 3

4 a² - 4ab + b²

25 х ² + 9 у ²

36a² + 4b²

4 х ² + 8 ху +4у ²

заполните таблицу

Квадрат

первого

выражения

( a+b ) ²

a²

Удвоенное

произведение

(m-n)²

(8-a)²

2ab

Квадрат

второго

выражения

Итог

2mn

64

(2x+3)²

b²

a²+2ab+ b²

9

m²-2mn+n²

n²

m²

64-16a+a²

16a

a²

4x²+12x+9

4x²

12x

П. 32. стр.153 – 154, выучить формулы и определения этих формул, выполнить

№ 817, № 831

СПАСИБО ЗА УРОК !!!