МКОУ «Ольховатская средняя общеобразовательная школа»
Научно-исследовательская работа
«Загадка чисел Фибоначчи»
Подготовил:
Бирюкова Ольга Юрьевна, обучающаяся 10 класса
Руководитель работы:
Никитина Оксана Анатольевна
учитель математики, МКОУ «Ольховатская средняя
общеобразовательная школа»
Курск, 2016
Оглавление
ВВЕДЕНИЕ…………………………………………………………………..4
ОСНОВНАЯ ЧАСТЬ
1. Биография Леонардо Пизанского (Фибоначчи).…………………………………………………………………6
2. История ряда Фибоначчи. …………………………………………………………………………….…..8
3. Числа Фибоначчи и их свойства. ………………………………………………………………………………..10
4. Числа Фибоначчи в окружающем нас мире
4.1. Числа Фибоначчи в растениях. …………………………………………………………………………..10
4.2. Числа Фибоначчи в строении животных.……………………………………………………………..12
4.3. Числа Фибоначчи в музыке. ………………………………………………………………………...12
4.4. Числа Фибоначчи в строении человека ………………………….......................................................................13
4.5. Числа Фибоначчи и золотой прямоугольник. ………………….……………………………………………………..14
5. Практическое исследование
5.1. Числа Фибоначчи в строении подсолнуха.……………………………………………………………..…15
5.2.Числа Фибоначчи в строении еловой и сосновой шишек…………………………………………………………….16
5.3.Числа Фибоначчи в строении ананаса……………………………………………………………16
5.4.Числа Фибоначчи в ветке дерева………………………………........................................….16
5.5.Числа Фибоначчи в строении кисти человека……………...………………………………………….17
5.6.Числа Фибоначчи в строении лица человека………………………………………………………...18
5.7.Числа Фибоначчи в спираль Фибоначчи в строении ракушки………………………………………………………...18
ЗАКЛЮЧЕНИЕ……………………………………………………........20
СПИСОК ЛИТЕРАТУРЫ………………………………………………………….22
ИНТЕРНЕТ РЕСУРСЫ………………………………………………………………..22
ПРИЛОЖЕНИЕ…………………………………………………………..24
ВВЕДЕНИЕ
«Неужели в каждом цветочке, и в молекуле, и в галактике,
числовые закономерности этой строгой «сухой» математики?».
Что такое числа Фибоначчи, где эти числа можно увидеть, где их можно встретить в нашей повседневной жизни, почему эта последовательность чисел столь распространена в нашем мире? Такие вопросы возникли, когда на уроке математики мы узнали о числах, которые называют «числами природы», образующих интересную последовательность, последовательность Фибоначчи.
Существует множество исследований, которые показывают где можно встретить последовательность Фибоначчи в самых разнообразных областях окружающей нас действительности. Нам захотелось прикоснуться к этим знаниям и провести своё исследование.
Результатом нашей теоретической и практической деятельности явилась данная исследовательская работа, тема которой «Загадка чисел Фибоначчи»».
Проблема, которую призвано разрешить наше исследование, заключается в том, что мы не знаем и не видим в окружающей нас жизни числовые закономерности, которые укладываются в ряд Фибоначчи.
Изучение этих чисел не предусмотрено уроками математики, поэтому чтобы познакомится с ними подробнее, необходимо использовать разнообразные источники информации: дополнительную литературу по предмету и интернет ресурсы.
Актуальность данного исследования заключается в том, что приобретаются новые знания, за рамками учебного предмета, знания которые необходимы каждому образованному человеку, потому что числа Фибоначчи встречаются ежедневно в окружающей нас действительности.
Цель исследования: изучение чисел Фибоначчи и их проявления в строении живых и неживых объектов.
Задачи работы:
Изучить литературу по данной теме.
Познакомиться с числами Фибоначчи и историей их создания.
Познакомиться с биографией итальянского математика Леонардо Пизанского (Фибоначчи).
Изучить свойства числового ряда Фибоначчи.
Найти описанные в литературе примеры чисел Фибоначчи в строении живых и неживых объектов.
Проверить на практике проявление чисел Фибоначчи в неживой природе, в строении человека и растений.
Познакомить с результатами исследования учащихся школы, учителей и родителей.
Объект исследования: числа Фибоначчи.
Предмет исследования: растения и тело человека.
Гипотеза: Мы предполагаем, что в окружающем нас мире многое построено с математической точностью и соответствует закономерности числового ряда Фибоначчи.
Методы исследования:
Теоретический.
Эмпирический (наблюдение, эксперимент, измерение).
Сравнение.
Классификация.
Математическое моделирование.
В теоретической части исследования мы изучили литературу по данной теме, узнали, как образуется этот ряд, историю его возникновения, какими свойствами он обладает. Рассмотрели разные объекты природы где, обнаруживает себя ряд Фибоначчи. Оказывается, эти числа можно найти в подсолнухах и сосновых шишках, в крыльях стрекозы и морских звёздах, в ритмах человеческого сердца и в музыкальных ритмах, в строении человеческого тела и в строении раковин моллюсков, в океане, в космосе и т.д. В проверке этих фактов заключается практическая часть нашего исследования.
Этапы исследования.
1. Подготовительный: выбор темы исследования, постановка проблемы, цели и задач исследования, выдвижение гипотезы, составление плана - графика работы,
2. Основной: изучение литературы по данной теме, сбор информации с использованием интернет ресурсов, проведение практических измерений и вычислений, анализ данных и их сравнение с уже известными научными фактами, выводы о состоятельности гипотезы и реализации задач исследования.
3. Заключительный: оформление исследовательской работы, создание слайдовой презентации, представление работы на школьной НПК и РНПК.
ОСНОВНАЯ ЧАСТЬ
1. Биография Леонардо Пизанского (Фибоначчи).
 Рис. 1.
Рис. 1.
Удивительные числа были открыты итальянским математиком средневековья Леонардо Пизанским, более известным под именем Фибоначчи. Леонардо Пизанский (Фибоначчи)– это первый крупный математик средневековой Европы. Более известен под прозвищем Фибоначчи, что в переводе с итальянского означает «хороший сын родился».
Точная дата его рождения неизвестна. Предположительно Фибоначчи родился в 1170г. в городе Пиза, в Италии. Леонардо из Пизы, известный как Фибоначчи, был первым из великих математиков Европы позднего Средневековья. Будучи рожденным в Пизе в богатой купеческой семье, он пришел в математику благодаря сугубо практической потребности установить деловые контакты [1].
Его отец был купцом и государственным вельможей, представителем нового класса бизнесменов. Тогда Пиза была одним из крупнейших коммерческих центров, активно сотрудничавших с исламским Востоком, и отец Фибоначчи энергично торговал на северном побережье Африки, по торговым делам часто бывал в Алжире. Благодаря этому ему удалось «устроить» своего сына в одну из арабских школ, где он смог получить превосходное для того времени математическое образование.
Леонардо изучал труды математиков востока, по арабским переводам он ознакомился также с достижениями античных и индийских математиков.
Все эти знания он впитывал в себя как губка. А потом принес их в Европу, он «открыл» арабские цифры вместо римских и десятичную систему счисления для европейцев. Значительную часть усвоенных им знаний он изложил в своей выдающейся «Книге абака» (Libег аЬасi, 1202; до наших дней сохранилась только дополненная рукопись 1228 г.). Эта книга содержит почти все арифметические и алгебраические сведения того времени, изложенные с исключительной полнотой и глубиной и одно из величайших открытий всех времён и народов – десятичную систему счисления.
На протяжении нескольких столетий по труду Фибоначчи ученые знакомились с двумя важнейшими разделами математики – арифметикой и алгеброй и черпали из него задачи и оригинальные методы решения, благодаря чему уже в XV – XVI в.в. те разошлись по многочисленным итальянским, французским, немецким, английским, а позже и русским рукописям, печатным книгам и учебникам.
Когда Леонардо вернулся в Италию, там правил император Фридрих II. Он не признавал рыцарские турниры, вместо них он проводил гораздо менее кровавые математические соревнования, на которых противники обменивались не ударами, а задачами. На таких турнирах и заблистал талант Леонардо Фибоначчи.
Предположительно Фибоначчи умер во время одного из Крестовых походов в 1228 году, сопровождая императора Фридриха II [1].
2. История ряда Фибоначчи.
Леонардо Фибоначчи совершил открытие чисел (впоследствии названных его именем) случайно. В 1202 году он пытался решить практическую задачу: какой максимальный приплод может дать одна пара кроликов за год и создать формулу, описывающую последовательность их размножения [1].
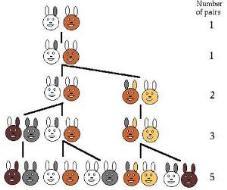 Рис. 2.
Рис. 2.
На второй месяц мы будем иметь одну пару, на третий месяц 1+1=2, на четвертый месяц 2+1=3 пары, на пятый месяц 3+2=5 пар, на шестой месяц 5+3=8 пар.
Разгадкой стал числовой ряд, каждое последующее число которого, является суммой двух предыдущих.
Отслеживая каждый месяц, количество пар кроликов получили такой ряд чисел:
1,1,2,3,5,8,13,21,34,55,89,144,233,377…
Таблица 1. Приплод кроликов по месяцам.
| Месяцы | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Пары кроликов | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 |
Ответ: 377 пар.
Числа, образующие данную последовательность называются "числами Фибоначчи", а сама последовательность - последовательностью Фибоначчи.
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, …
3. Числа Фибоначчи и их свойства.
После изучения исторических сведений, началась практическая часть нашего исследования.
Узнав, как образуется числовой ряд Фибоначчи, мы вычислили первые шестьдесят чисел. Получился следующий ряд:
1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 2584 4181
6765 10946 17711 28657 46368 75025 121393 196418 317811 514229 832040 1346269 2178309 3524578 5702887 9227465 14930352 24157817 39088169
63245986 102334155 165580141 267914296 433494437 701408733 1134903170
1836311903 2971215073 4807526976 7778742049 12586269025 20365011074
32951280099 53316291173 86267571272 139583862445 225851433717 36543529612 591286729879 956722026041 1548008755920 …
Установлены следующие свойства:
1 .Каждое следующее число, начиная с третьего, равно сумме двух предыдущих
3+5=8 13+21=34 и т.д.
Отношение каждого числа к последующему при увеличении порядкового номера всё более и более стремится к 0.618.
13:24=0.619 21:34=0.618
Частное от деления последующего числа Фибоначчи на предыдущее, по мере роста самих чисел, стремиться к 1,618.
233 / 144 = 1,618
377 / 233 = 1,618
610 / 377 = 1,618
987 / 610 = 1,618
1597 / 987 = 1,618
2584 / 1597 = 1,618
Сколько бы раз мы не делили одно на другое, соседнее с ним число, мы всегда получим 1, 618.
Каждое третье число Фибоначчи четное (выделено красным).
Каждое пятнадцатое оканчивается нулем (подчеркнуто).
4. Числа Фибоначчи в окружающем нас мире.
4.1. Числа Фибоначчи в растениях.
С тех пор, как Фибоначчи открыл свою последовательность, были найдены много явлений природы, в которых его последовательность чисел прослеживается очень четко. Природа дает нам многочисленные примеры расположения предметов, описываемых числами Фибоначчи. Спиралевидное расположение листьев на ветках деревьев подметили давно. Выяснилось, что в расположении листьев на ветке (филлотаксис - листорасположение), в числе оборотов на стебле, в числе листьев в цикле проявляет себя ряд чисел Фибоначчи [2].

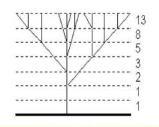 Рис. 3.
Рис. 3.
Чёткая, симметричная форма цветов также подчинена строгому закону.
У многих цветов количество лепесточков является числами из ряда Фибоначчи. Например:




Ирис. 3лепестка Лютик. 5 лепестков Златоцвет. 8 лепестков Дельфиниум.
13 лепестков



Цикорий.21лепесток Астра. 34 лепестка Маргаритка.55лепестков Рис. 4.
Встретить числовые закономерности в живой природе можно в различных спиральных формах, которыми так богат мир растений. Обычно можно усмотреть два вида спиралей. В одном спирали завиваются по часовой стрелке, а в другом против. Число "правых "и "левых" спиралей часто оказываются соседними числами Фибоначчи [2], [5].
Можно привести множество примеров.
Семена в подсолнухе распределяются по спирали (рис. 5). Они растут по и против часовой стрелки от центра цветка.. Количество этих спиралей – это два числа, идущих подряд в последовательности Фибоначчи 21 и 34 или 34 и 55. Особенно много спиралей можно наблюдать в расположении семечек крупного подсолнуха. Их число в каждом из направлений может достигать 55 и 89.


Подсолнечник. 21 и 34 спирали. Эхинацея. 34 и 55 спиралей. Рис.5.
Колючки ананаса образуют два множества спиралей: 8 спиралей идут по часовой стрелке, а 13 спиралей идут против часовой стрелки.


Рис. 6.
Чешуйки в хвойных шишках (рис. 6) "упакованы" по спиралям, завивающимся навстречу друг другу, причем их количество всегда выражается соседними числами Фибоначчи. В крупных шишках удается наблюдать 5 и 8 и даже 8 и 13 спиралей, на ананасе: обычно их бывает 8 и 13 [2], [5], [7], [9].
4.2. Числа Фибоначчи в строении животных.
Кроме растений, числа Фибоначчи проявляются в строении различных живых организмов. Например, морские звезды. Число лучей у них отвечает ряду чисел Фибоначчи и равно 5, 8, 13.
У хорошо знакомого комара – три пары ног, брюшко делится на 8 сегментов на голове 5 усиков – антенн (рис. 7). И опять мы видим числа 3,5,8, числа последовательности Фибоначчи.


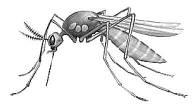 Рис. 7. Строение комара.
Рис. 7. Строение комара.
4.3. Числа Фибоначчи в музыке.
Числа Фибоначчи можно встретить и в музыке. Одна октава на клавишной панели пианино состоит из 13 клавиш: 8 белых и 5 чёрных, которые разбиты на группы по 3 и 2. Все эти числа являются числами Фибоначчи [2], [5].
4.4. Числа Фибоначчи в строении человека.
Числа Фибоначчи отражают основную закономерность роста организмов, следовательно проявляются и в строении человеческого тела. Рассмотрим это поподробнее.
У человека одно туловище, одна голова, одно сердце и т. д. Многие части тела и органы парные, например, руки, ноги, глаза, почки. Из трех частей состоят ноги, руки, пальцы рук. На руках и ногах по пять пальцев, а рука вместе с пальцами состоит из восьми частей.
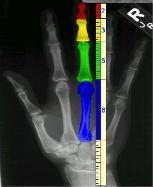 Рис.8.
Рис.8.
Можно рассмотреть части тела и с другой стороны (рис. 8.). У человека 2 руки, пальцы на каждой руке состоят из 3 фаланг (за исключением большого пальца). На каждой руке имеется по 5 пальцев, только 8 пальцев трехфаланговые. Все эти цифры 2, 3, 5 и 8 есть числа последовательности Фибоначчи.
Позвоночник человека состоит из 34 позвонков. Как видно из приведенного перечисления частей человеческого тела, в его членении на части присутствуют все числа Фибоначчи от 1 до 34.
Общее число костей скелета человека близко к 233, то есть отвечает еще одному числу Фибоначчи.
Числа Фибоначчи можно обнаружить и в «крови» у человека. Так распределение людей по трём группам крови отвечает отношениям чисел 8/ 21 /34.
Сердечная мышца сокращается до 0,618 от своей изначальной длины и нарушение этого числа при сокращении ведет к болезням сердца. А это число отражает одно из свойств чисел Фибоначчи.
В результате математической обработки экспериментальных медицинских данных, появились отношения чисел, характеризующих сердечный цикл: 0,050; 0,081; 0,131; 0,210; 0,340. Мы видим, что они отражают последовательность ряда чисел Фибоначчи 5, 8, 13, 21, 34.
В строении человеческого лица и кисти существуют и иные воплощения ряда Фибоначчи.
Этот ряд получается, если провести измерения длин фаланг пальцев (рис.9.) и расстояний между различными частями лица (рис.10.) [7], [10].
 Рис. 9 .
Рис. 9 .  Рис. 10.
Рис. 10.
4.5. Числа Фибоначчи и золотой прямоугольник.
Мы уже отмечали, что числа Фибоначчи тесно связаны со спиралевидным строением многих представителей живой и неживой природы. Чтобы рассмотреть еще несколько таких примеров, необходимо познакомиться с так называемым «золотым прямоугольником» (рис.11.). Золотой прямоугольник обладает многими необычными свойствами. Отрезав от золотого прямоугольника квадрат, сторона которого равна меньшей стороне прямоугольника, мы снова получим золотой прямоугольник меньших размеров.
Этот процесс можно продолжать до бесконечности. Продолжая отрезать квадраты, мы будем получать все меньшие и меньшие золотые прямоугольники. Причем располагаться они будут по спирали (рис.12.), которая называется спираль Фибоначчи.
 Рис.11.
Рис.11.  Рис.12..
Рис.12..
Эту спираль можно обнаружить в самых различных и неожиданных предметах и явлениях.

 Рис.13.
Рис.13.
У большинства улиток, которые обладают раковинами, раковина растет в форме спирали. Раковины улиток подчиняются последовательности и спирали Фибоначчи.
Паук плетет паутину спиралеобразно. Интересно, что спиралью закручиваются ураган, облака циклона и это хорошо видно из космоса [6], [10].
| 
| 
|
| Рис 14. Паутина. | Рис 15. Ураган.
|

Рис.16. Облака циклона
Числа Фибоначчи оказались и в спирали, описывающей изгиб гребня набегающей волны в океане, и в спирали, убегающей воды в раковине умывальника. Да и живём мы тоже в спирали, ведь галактика – это спираль, соответствующая спирали Фибоначчи (рис.19).
 Рис.17.
Рис.17.  Рис.18. .
Рис.18. . Рис. 19
Рис. 19
5. Практическое исследование.
Вторая часть нашего практического исследования заключается в конкретных подсчетах и измерениях.
5.1. Числа Фибоначчи в строении подсолнуха.
Первым для изучения мы взяли подсолнух и сосчитали количество спиралей, идущих в одну сторону и количество спиралей в другую сторону. Правых спиралей, они закрашены красным, получилось 34, левых, они закрашены синим – 55 (рис.20.). Эти числа 34 и 55 являются соседними в последовательности Фибоначчи.
. Рис. 20.
Рис. 20.
Расположение семян подсолнуха
5.2.Числа Фибоначчи в строении еловой и сосновой шишек.
Продолжая исследование, числа, входящие в ряд Фибоначчи мы увидели в сосновых и еловых шишках. Подсчет спиралей выявил следующие результаты. Замечаем две серии спиралей Фибоначчи: одна - по часовой стрелки, другая - против, их число 8 и 13.
 Фото 1. Еловая шишка.
Фото 1. Еловая шишка.  Рис. 21.Сосновая шишка.
Рис. 21.Сосновая шишка.
5.3.Числа Фибоначчи в строении ананаса.
На фотографиях показано как мы проводили подсчеты чешуек на кожуре ананаса. Нами получены числа: 8 и 13. Как мы снова можем убедиться, эти числа являются членами последовательности Фибоначчи.
 Фото 2. Фото 3. Работа с ананасом
Фото 2. Фото 3. Работа с ананасом
5.4.Числа Фибоначчи в ветке дерева.
Последовательность ответвлений, идущих по стволу растений, мы подсчитывали, рассматривая ветку дерева. Положив её на ватман, мы провели горизонтальные линии, соответствующие пазам выхода веток, и посчитали их количество. Получили следующие данные: 1,2,3,5,8… Полученный ряд является частью ряда Фибоначчи.
Фото 4. Работа с веткой дерева.  Фото 5.
Фото 5.
5.5.Числа Фибоначчи в строении кисти человека.
 Рис.22
Рис.22
В следующей части практических измерений мы исследуем строение кисти рук наших одноклассников и проверим справедливость равенства a = b+c (рис. 22). Для этого мы измеряли длину 1,2 и 3 фаланги пальцев и длину от 3 фаланги до запястья (фото 6.)

 Фото 6.
Фото 6.
Результаты измерений занесены в таблицу.
| Рука Имя | 1 фаланга (мм) | 2 фаланга (мм) | 3 фаланга (мм) | От 3 фаланги до запястья (мм) |
| Настя | 16 | 25 | 41 | 66 |
| Лиза | 23 | 25 | 48 | 72 |
| Тая | 20 | 25 | 45 | 70 |
| Кирилл | 20 | 25 | 45 | 71 |
Таблица 2. Результаты измерений кисти рук. Анализируя полученные результаты, можно заметить, что данные числа соответствуют правилу, по которому образуются числа Фибоначчи: каждое следующее число равно сумме двух предыдущих чисел. 16+25=41, 25+41=66, 23+28=48, 25+48=72, 20+25=45, 25+45=70 и т.д.
5.6.Числа Фибоначчи в строении лица человека.
Проверку соответствия ряду Фибоначчи строения лица человека, мы проводили на своих одноклассниках. У каждого из них мы измерили высоту подбородка, расстояние от верхней губы до носа, расстояние от носа до бровей, высоту лба. Результаты измерений представлены в таблице.
Таблица 3. Результаты измерений лица.
| Высота подбородка | Расстояние от верхней губы до носа | Расстояние от носа до бровей | Высота лба |
| 20 | 28 | 40 | 56 |
| 40 | 20 | 60 | 80 |
| 33 | 25 | 57 | 83 |
| 35 | 25 | 60 | 78 |
В результате проведенных опытов, мы еще раз убедились, что в строении лица человека также присутствует стремление к правилу, по которому образован ряд Фибоначчи.
5.7.Числа Фибоначчи в спираль Фибоначчи в строении ракушки.
На следующем этапе нашего практического исследования, мы рассматривали строение ракушки и её соответствие спирали Фибоначчи и золотому прямоугольнику. Сначала мы сами построили этот прямоугольник, для того, чтобы понять принцип его образования.
Затем получили его на фотографии ракушки. Мы рассматривали две различные раковины (фото 8.) и «уложили» их спирали в золотой прямоугольник (фото 9.). На последнем фото хорошо видно, что стороны прямоугольника образуют ряд чисел 3,5,8,13,21,34,55… , которые являются членами последовательности Фибоначчи.

 Фото 8.
Фото 8.  Рис.22
Рис.22
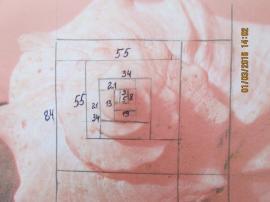
 Фото 9.
Фото 9.
ЗАКЛЮЧЕНИЕ
Исследование по теме «Загадка чисел Фибоначчи» состояло из двух частей: теоретической и практической. В теоретической части мы изучили литературу по данной теме. Узнали, какие числа образуют последовательность Фибоначчи, познакомились с историей их открытия. Вместе с тем мы изучили свойства числового ряда Фибоначчи и его закономерности. Познакомились с биографией итальянского математика Леонардо Пизанского (Фибоначчи), чьё имя носит эта замечательная последовательность. Используя различные источники информации, мы изучили проявление чисел Фибоначчи в окружающей нас действительности, в живой и неживой природе. Так мы узнали, что закономерности этого числового ряда проявляются в числе спиралей у растений, в расположении семян подсолнуха, в сосновых и еловых шишках, в строении кожуры ананаса, в расположении пазов веток деревьев. Этому же закону подчиняется количество лепестков в цветах растений. Неожиданным для нас в этом исследовании было то, что числа Фибоначчи проявляют себя и в музыке, и в ритме сердца, и в сокращении сердечной мышцы. Также мы увидели строгую математику в строении человеческого тела. Кроме этого узнали такое понятие как «золотой» прямоугольник, и как образуется спираль Фибоначчи. По этой спирали закручены раковины улиток, волны океана, ураган, облака циклона и галактики.
В практической части нашего исследования проводилась проверка на практике проявлений чисел Фибоначчи в неживой природе, в строении человека и в строении растений. Мы провели подсчеты количества спиралей в еловой и сосновой шишках, подсчитали их количество в расположении семян подсолнуха и в пазах ветки дерева, и опытным путем убедились, что все полученные числа образуют ряд Фибоначчи. Кроме этого мы провели измерения лица и кисти рук у четверых наших одноклассников. В результате получили ряд чисел, каждое из которых равно сумме двух предыдущих. А это основной принцип образования последовательности Фибоначчи. Последним этапом практической части исследования и самым трудным было установить соответствие между спиралью ракушки и размерами «золотого» прямоугольника. И здесь нам удалось «уложить» изображение ракушки в этот прямоугольник, и тем самым показать, что спираль ракушки является спиралью Фибоначчи.
В процессе исследования было установлено, что числовой ряд Фибоначчи характеризует структуру многих объектов живой и неживой природы. В результате мы реализовали все поставленные задачи и достигли основной цели исследования. Таким образом, наша гипотеза о том, что в окружающем нас мире многое построено с математической точностью и соответствует закономерности числового ряда Фибоначчи полностью подтвердилась. Строение многих встречающихся в природе живых организмов и неживых объектов, не имеющих связи между собой, обнаруживает удивительную математическую закономерность, которая описывается последовательностью чисел Фибоначчи.
Необходимо отметить практическая значимость работы: результаты данного исследования можно использовать как дополнительный материал на уроках математики, в кружковой работе и предметных неделях, в проектной деятельности по другим предметам. Приобретенные навыки исследовательской работы пригодятся при изучении других школьных предметов.
Самим творцом во все объекты
Заложен уникальный код,
И тот, кто дружен с математикой,
Его познает и пой
СПИСОК ЛИТЕРАТУРЫ
Воробьев Н. Н. Числа Фибоначчи. – М., Наука, 1984.
Гика М. Эстетика пропорций в природе и искусстве. – М., 1936.
Дмитриев А. Хаос, фракталы и информация. // Наука и жизнь, № 5, 2001.
Кашницкий С. Е. Гармония, сотканная из парадоксов // Культура и
жизнь. – 1982.– № 10.
Малай Г. Гармония – тождество парадоксов // МН. – 1982.– № 19.
Соколов А. Тайны золотого сечения // Техника молодежи. – 1978.– № 5.
Стахов А. П. Коды золотой пропорции. – М., 1984.
Урманцев Ю. А. Симметрия природы и природа симметрии. – М., 1974.
Урманцев Ю. А. Золотое сечение // Природа. – 1968.– № 11.
Шевелев И.Ш., Марутаев М.А., Шмелев И.П. Золотое сечение. Три
взгляда на природу гармонии.- М., 1990.
Шубников А. В., Копцик В. А. Симметрия в науке и искусстве. - М.:
Наука, 1972.
ИНТЕРНЕТ РЕСУРСЫ
1.http://www.chydesa-sveta.ru/en/chisla_fibonachchi.html
2.http://zagadkamozga.ru/node/630
3.http://magov.net/blog/3621.html
4.http://greenword.ru/2009/06/fibonacci-sequence.html
5.http://esopedia.ru/ChislaFibonachchi
6.http://reflection.org.ua/vselennaya/zagadka-chisel-fibonachi.html
7.http://dip-ref.ru/diplom/778.htm
8.http://evolutionoftruth.com/abennett
9.http://evolutionoftruth.com/goldensection/solarsys.htm
10.http://www.goldenmuseum.com/
11.http://www.mcs.surrey.ac.uk/Personal/R.Knott
12.http://goldennumber.net/
Приложение































 Рис. 10.
Рис. 10.
 Рис.12.
Рис.12.





 Рис.18. .
Рис.18. . Рис. 19
Рис. 19  Рис. 20.
Рис. 20. 
 Рис. 21.Сосновая шишка.
Рис. 21.Сосновая шишка.






 Рис.22
Рис.22

















