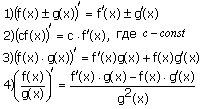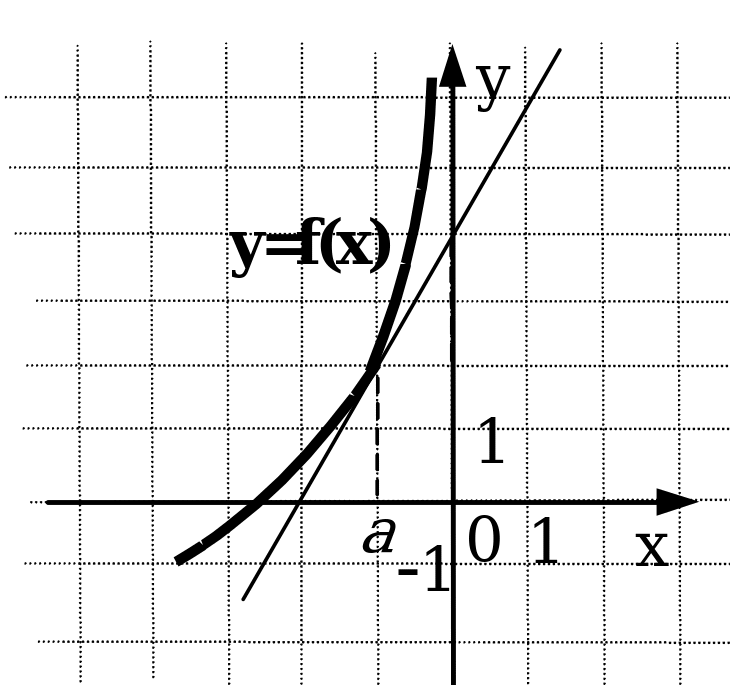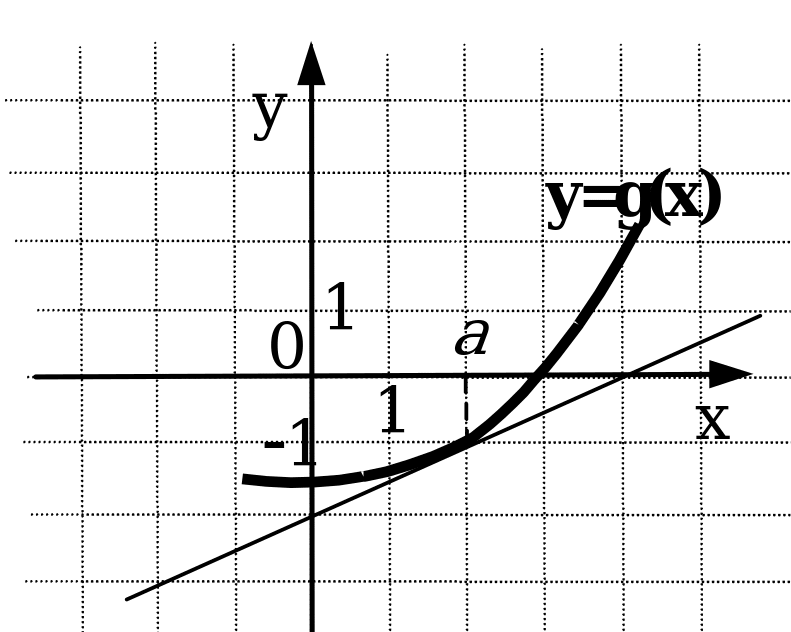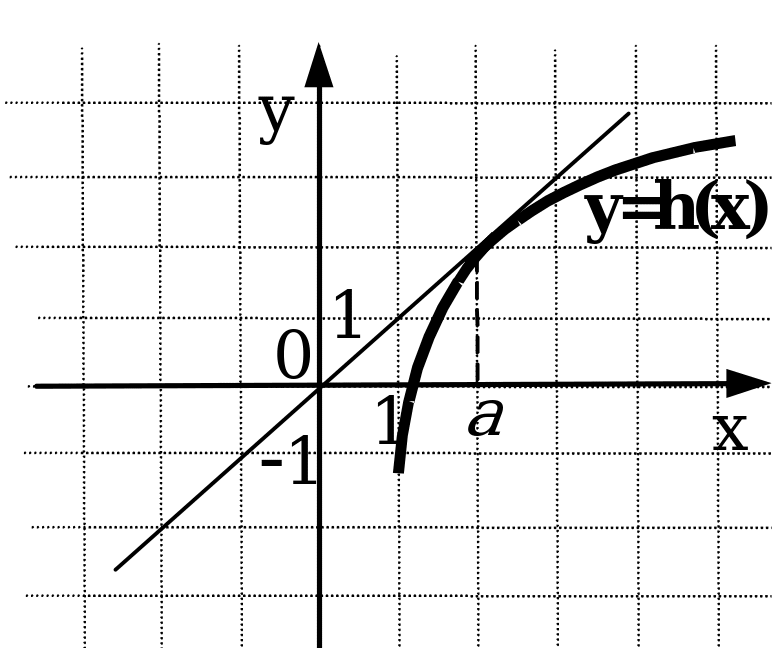Учитель математики сш им Досова Колесникова Л.А
"Вычисление производных"- открытый урок в 10 класс
Цели урока:
Обобщить и оценить знания учащихся по данной теме
Проверить умения учащихся применять формулы и правила вычисления производных
Развивать мышление, речь, умение комментировать, тренировать память
Воспитывать трудолюбие, чувство товарищества и взаимопомощи
Прививать интерес к предмету путем дружеского соперничества .
Методы и приемы: словесный, наглядный, практический.
По типу: урок обобщения и систематизации знаний.
Оборудование: раздаточный материал (разноуровневые карточки с практическими заданиями, листы учета знаний), интерактивная доска..

Ход урока
1 ЭТАП. Организационный момент
Эпиграфом к сегодняшнему уроку будут слова Ньютона “При изучении наук примеры не менее поучительны, нежели правила” и слова Ломоносова “Примеры
учат больше, чем теория”.




2.этап.
из истории математики.
Исторические сведения
Дифференциальное исчисление было создано Ньютоном и Лейбницем в конце 17 столетия на основе двух задач:
1) о разыскании касательной к произвольной линии
2) о разыскании скорости при произвольном законе движения
Еще раньше понятие производной встречалось в работах итальянского математика Тартальи (около 1500 - 1557 гг.) - здесь появилась касательная в ходе изучения вопроса об угле наклона орудия, при котором обеспечивается наибольшая дальность полета снаряда.
В 17 веке на основе учения Г.Галилея о движении активно развивалась кинематическая концепция производной. Различные изложения стали встречаться в работах у Декарта, французского математика Роберваля, английского ученого Л. Грегори. Большой вклад в изучение дифференциального исчисления внесли Лопиталь, Бернулли, Лагранж, Эйлер, Гаусс.

3 этап.
Актуализация опорных знаний.
На данном этапе предлагается следующее:
1. Электронный кроссворд " Мысли в фокус"
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 15 | | | | | | | |
|
|
|
|
| 11 |
|
|
|
|
| 1 |
|
|
|
| 9 |
|
|
|
|
|
|
|
| |
|
|
| 14 |
| |
| 8 | | | | | | | | |
|
|
| |
|
|
| |
| |
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
| |
| |
|
| 12 | | | | | | | |
| 3 |
| |
|
| 6 | | | | | |
|
| |
|
|
|
|
|
| |
| |
|
|
| |
| |
|
| 4 | | | | | | | 13 | | | | |
|
|
| |
| |
|
|
|
| |
|
|
|
|
|
| |
| |
|
|
|
|
| |
| 10 | | | | | | | | |
| |
|
|
|
|
|
|
| |
|
|
|
| |
|
|
|
|
|
| |
|
|
|
| 5 | | | | |
|
|
| | 2 | | | | | | | |
|
|
|
|
|
| |
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
|
| |
|
|
|
| | 7 | | | | |
| |
|
|
1. Угол ее наклона выражает геометрический смысл производной.
2. Великий немецкий ученый, философ, математик, физик, юрист, языковед,
создатель математического анализа, основоположник большой математической школы.
3. Раздел физики, помогающий понять смысл производной.
4. Точка интриганка, точка … .
5."Microsoft Windows в переводе на русский "Компания …"
6. Имя английского физика и математика, автора сочинения "Математические начала натуральной философии"
7. Маленькая, серенькая на коврике лежит. Что это?
8. Утверждение, которое в ходе исследовательской работы подтверждается или опровергается.
9. Синоним понятию "дифференциальное исчисление"
10. Производная- это….
11. Внешний носитель информации в компьютере.
12. Устройство вывода информации в компьютере.
13. Одна из эффективных форм проверки знаний учащихся.
14. "Любите … - источник знаний".
15. Соответствие, при котором каждому числу х из множества D сопоставляется по некоторому правилу число y, зависящее от х.
3 этап
"Своя игра".
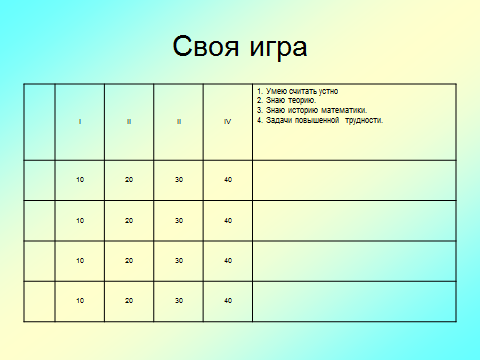
Умею считать устно.

1. Найти производную функции
) у = 4х2 + 5х + 8 и найти её значение в точке х0 = 2.
(ответ: 21)
2. Какой угол (острый или тупой) образует касательная, проведенная к графику функции 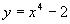 в точке с абциссой
в точке с абциссой 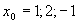 с осью ОХ (ответ: острый, острый, тупой).
с осью ОХ (ответ: острый, острый, тупой).
3. Дана функция 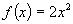 Решить уравнение:
Решить уравнение: 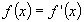 (ответ: 0; 2)
(ответ: 0; 2)
4. Найти производную функции у=2√х
Ответ 
Знаю теорию.
1. Что называется производной функции в точке?
Ответ: производной функции у = f(x) в точке х0 называется предел отношения
приращения функции в точке х0 к приращению аргумента, когда последнее стремится к нулю.
2. ) В чем заключается геометрический смысл производной?
Ответ: значение производной f '(x) при данном значении аргумента x равно тангенсу угла,
образованного с положительным направлением оси Ox касательной к графику функции f(x) в
точке M(x, f(x)). k = tg = f '(x0).
3. ) В чем заключается механический смысл производной?
Ответ: производная функции y = f(x) в точке x0 - это скорость изменения функции f (х) в
точке x0 x'(t). = (t)

4. Правила дифференцирования.
Если у функций f(x) и g(x) существуют производные, то
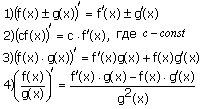
Знаю историю математики.
1. Кто ввел знак для обозначения производной? (Лагранж)
2. Назовите 2-3 фамилии ученых-математиков, с именами которых связаны исследования в области дифференциального исчисления (Ферма, Вейерштрасс, Нью тон, Лейбниц).
3. Когда возникло понятие производной и в связи с решением каких задач физики, математики? (В XVII в. в связи с решением двух задач: определения скорости прямолинейного неравномерного движения; построения касательной к произвольной плоской кривой).
4. Что такое “флюэнта” и “флюксия”? (По Ньютону “флюэнта” – функция, “флюксия” – производная функции).

Задачи повышенной трудности.
у = -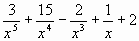 ответ.
ответ.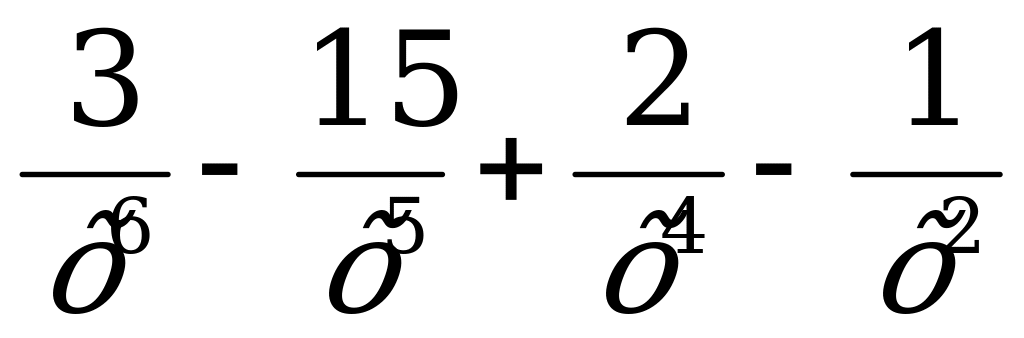
у= 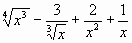
у = (х3 – 1)(х2 + х + 1 )
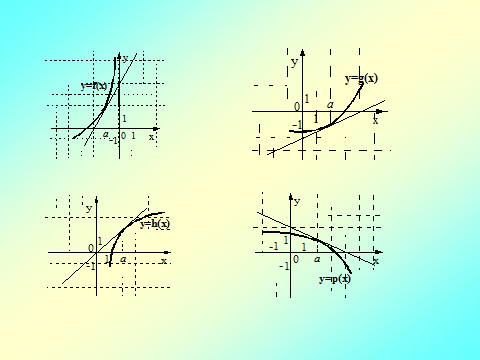
4. На рисунках изображены графики функций и касательные к ним в точке а. Укажите функцию, производная которой в точке а равна 1.
Ответ: (3)

|
| I | II | II | IV | |
| | 10 | 20 | 30 | 40 | |
| | 10 | 20 | 30 | 40 | |
| | 10 | 20 | 30 | 40 | |
| | 10 | 20 | 30 | 40 | |
3. Интерактивный тест
Учитель математики:
Найти соответствие между функцией и её производной.
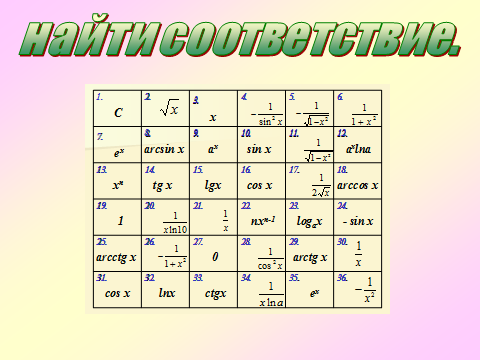
Ответ. 1-27, 2-17, 3-19, 13-22, 21- 30-36
Самостоятельная работа. ( приложение №1)
подведение итогов.
домашнее задание.