Разработка урока "Правильные многогранники" (11 класс).

Тема: Правильные многогранники

Контингент учащихся: 11 класс

Время проведения, общая продолжительность: 2 урока по 45 мин

Оборудование и материалы: компьютер, проектор, презентация, раздаточный материал, (приложения 1,2), клей, модели правильных многогранников, математическая энциклопедия, математический словарь для школьника, учебник Геометрия 10 - 11 класс.

Основная форма проведения занятия: семинар – практикум.

Методы и приемы обучения: групповая работа, самостоятельная работа, работа со справочной литературой, совместное принятие решений.

Цель учебного занятия: создание условий для формирования понятия правильного многогранника, для получения знаний о свойствах многогранников и представления о связи математики с окружающим миром. Способствовать развитию пространственного воображения у обучающихся Воспитывать   графическую культуру, умения работать в группе

Ожидаемые результаты – развиваемые компетенции:

1. Предметные: умение самостоятельно искать, анализировать, отбирать, преобразовывать необходимую информацию. Выполнять вычисления, преобразование формул. Заполнять таблицу.

2. Метапредметные: умение работать со справочной литературой, умение учиться и оперировать знаниями, навыки использования компьютерных технологий.

3. Личностные: готовность осуществлять интеллектуальное саморазвитие,

4. Коммуникативные: умение работать в группах, владение различными ролями в коллективе, умение задавать вопрос, вести дискуссию.

1. Содержание занятия

2.1 Мотивирующий этап (5 мин)

Учитель: Мне хотелось бы начать со слов Бертрана Рассела: "Математика владеет не только истиной, но и высшей красотой - красотой отточенной и строгой, возвышенно чистой и стремящейся к подлинному совершенству, которое свойственно лишь величайшим образцам искусства”. Есть в школьной геометрии особые темы, которые ждешь с нетерпением, предвкушая встречу с невероятно красивым материалом. К таким темам можно отнести тему "Правильные многогранники". Здесь не только открывается удивительный мир геометрических тел, обладающих неповторимыми свойствами, но и интересные научные гипотезы. Ни одни геометрические тела не обладают таким совершенством и красотой, как правильные многогранники. Сегодня на уроке мы узнаем и увидим много интересного, нам предстоит ответить на такие вопросы, как, например: Какие многогранники называются правильными? Сколько их существует? Что такое Эйлерова характеристика? И многие - многие другие. И, наконец: где, зачем и для чего нам нужны многогранники? Может быть, в жизни можно обойтись и без них? Данный материал пригодится нам при изучении темы "Объемы многогранников» и при решении задач на комбинацию геометрических тел.

Все правильные многогранники были известны еще в Древней Греции, и им посвящена заключительная, 13-я книга знаменитых "Начал” Евклида. Название "правильные” идет от античных времен, когда стремились найти гармонию, правильность, совершенство в природе и человеке. Как говорилось раньше, эти многогранники часто называют также платоновыми телами – в идеалистической картине мира, данной великим древнегреческим мыслителем Платоном, четыре из них олицетворяли 4 стихии: один – огонь, другой – землю, третий – воду, четвёртый – воздух, пятый же многогранник символизировал все мироздание – его по-латыни стали называть quinta essentia (квинта эссенция), означающее все самое главное, основное, истинную сущность чего-либо.

ПРАВИЛЬНЫЙ МНОГОГРАННИК - выпуклый многогранник, грани которого являются правильными многоугольниками с одним и тем же числом сторон и в каждой вершине которого сходится одно и тоже число ребер.(Презентация)

2.2 Основной этап (30 мин)

Работа в группах. Деление на группы производится заранее, учитывая уровень подготовки детей, так же их желание. Задания для групп: используя компьютер, справочную литературу, учебник и модели многогранников, находящихся в учебном кабинете ответить на вопросы, заполнить таблицу и создать презентацию. (приложение 1)

Основное оценочное средство: тесты действий.

1. Сколько существует правильных многогранников? Почему? Каковы их названия?

2. Из каких правильных многоугольников составлена их поверхность? Найти развертки правильных многогранников. Как найти площадь поверхности правильного многогранника?

3. В чём заключается теорема Эйлера?

4. Проверить теорему Эйлера для правильных многогранников. Заполнить таблицу.

5. Привести примеры существования правильных многогранников в окружающем мире.

Отчет групп о работе (20 минут). Один – два представителя группы отчитываются о результатах работы у доски поочерёдно по каждому вопросу, другие добавляют и исправляют.

Учащиеся делают соответствующие записи в тетради.

• теорему Эйлера;

• проверяют заполненную таблицу.

• формулы площади поверхности правильных многогранников ;

Число вершин минус число рёбер плюс число граней равно двум.

Число В-Р+Г называется эйлеровой характеристикой многогранника. Согласно теореме Эйлера, для выпуклого многогранника эта характеристика равна 2. То ,что эйлерова характеристика равна 2 для некоторых знакомых нам многогранников, видно из таблицы.

Развертки.

Закрепление (30мин)

Первичное закрепление

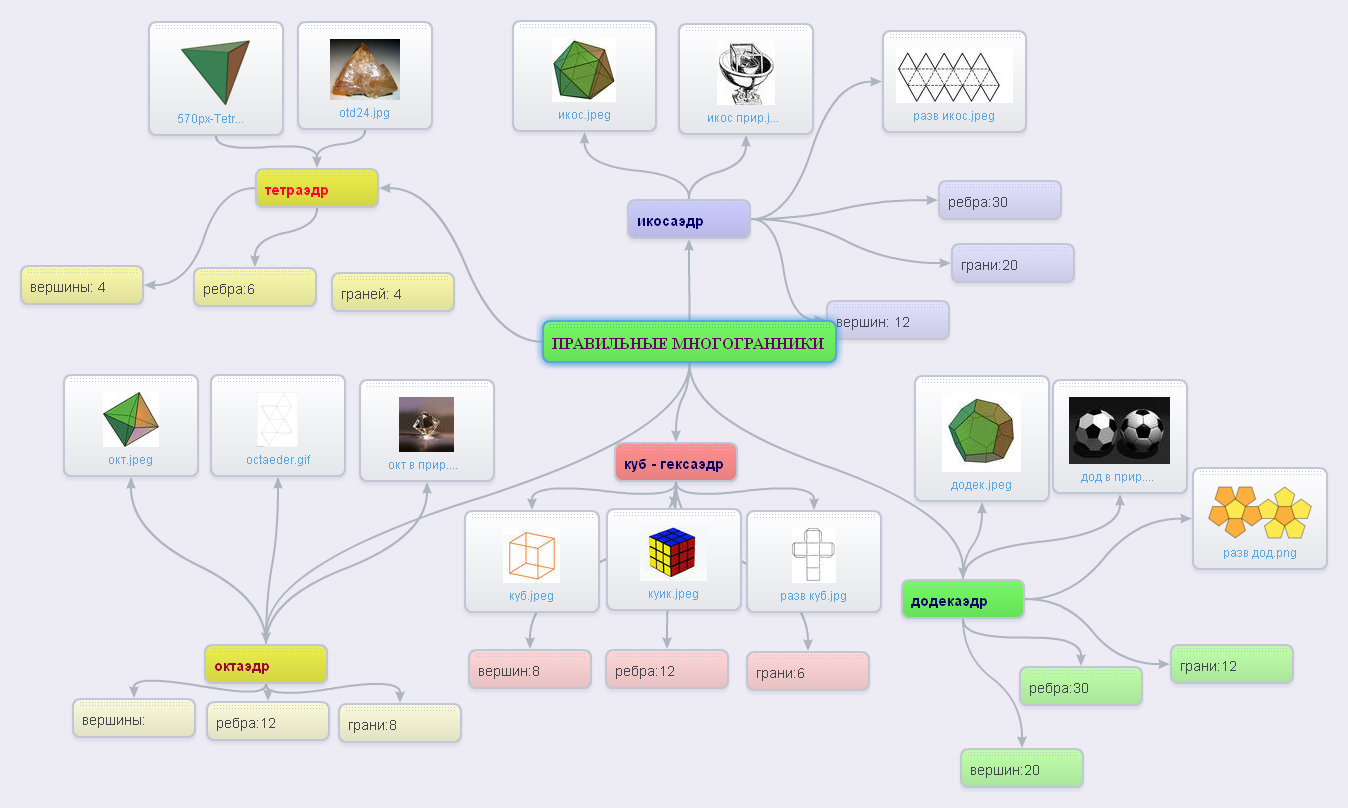
Создание кластера Правильные многогранники. (Приложение 2)

Решение задач. Работают самостоятельно.

1. Найти площадь поверхности октаэдра ребро которого равно 3 см.(18√3 )

2. Найти диагональ куба площадь поверхности которого 24 см².(2√2)

3. Найти площадь поверхности додекаэдра ребро которого равно 12 см.(180tg54⁰)

Обсуждение результатов решения задач.

Домашнее задание(3мин)

1. Подготовить сообщения-презентации по темам:

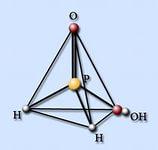
Правильные многогранники и химия.

Правильные многогранники в биологии.

Искусство и правильные многогранники.

Ювелирные украшения.

Икосаэдро-додекаэдровая структура Земли

1. Изготовить модель правильного многогранника

1. Оценка компетенций обучающихся. Заполнение карты оценки компетенций.

Карта оценки уровня сформированности компетенций обучающихся

с использованием теста действий.

1. Рефлексия хода и результатов занятия. (2мин)

1. Что понравилось на уроке?

2. Что нового вы узнали?

3. Какой материал был наиболее интересен?

4. Оцените свою работу на уроке: плохо работал, хорошо, отлично.

5. Связь геометрии, с какими науками вы увидели сегодня на уроке?

6. В каких еще областях деятельности можно встретиться с правильными многогранниками?

Приложение 1

Ответить на вопросы

1. Сколько существует правильных многогранников? Каковы их названия?

2. Из каких правильных многоугольников составлена их поверхность? Как найти площадь поверхности правильного многогранника?

3. В чём заключается теорема Эйлера?

4. Проверить теорему Эйлера для правильных многогранников. Заполнить таблицу.

5. Привести примеры существования правильных многогранников в окружающем мире.

Заполнить таблицу.

Решите задачи самостоятельно.

1. Найти площадь поверхности октаэдра ребро которого равно 3 см.

2. Найти диагональ куба площадь поверхности которого 24 см².

3. Найти площадь поверхности додекаэдра ребро которого равно 12 см.

Обсуждение результатов решения.

Приложение 2 Заполните кластер.

рисунок

Правильные многогранники

ПРИЛОЖЕНИЕ2

Раздаточный материал для создания кластера

Правильные многогранники

Математика владеет не только истиной, но и высшей красотой - красотой отточенной и строгой, возвышенно чистой и стремящейся к подлинному совершенству, которое свойственно лишь величайшим образцам искусства.

Бертран Рассел

Определение: выпуклый многогранник называют правильным если , все его грани равные правильные многоугольники и в каждой вершине сходится одинаковое количество ребер.

Работа в группах

Предмет математики столь серьезен, что не следует упускать ни одной возможности сделать его более занимательным.

(Б. Паскаль)

Платон считал, что мир строится из четырёх «стихий» - огня, земли, воздуха и воды, а атомы этих «стихий» имеют форму четырёх правильных многогранников. Тетраэдр олицетворял огонь, поскольку его вершина устремлена вверх, как у разгоревшегося пламени; икосаэдр – как самый обтекаемый – воду; куб – самая устойчивая из фигур – землю, а октаэдр – воздух.

Пятый многогранник – додекаэдр символизировал весь мир и почитался главнейшим.

Вывод:

• благодаря правильным многогранникам открываются не только удивительные свойства геометрических фигур, но и пути познания природной гармонии.

Домашнее задание.

• Подготовить сообщения-презентации по темам:
• Правильные многогранники и химия.
• Правильные многогранники в биологии.
• Искусство и правильные многогранники.
• Ювелирные украшения.
• Икосаэдро-додекаэдровая структура Земли
• Изготовить модель правильного многогранника.