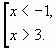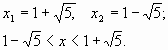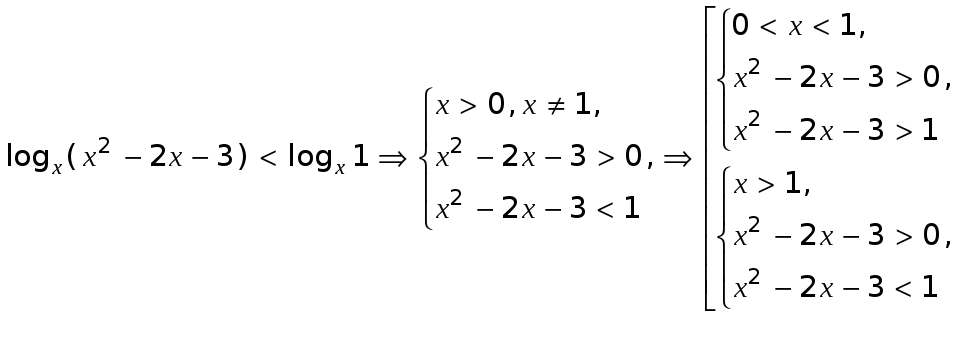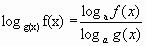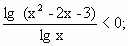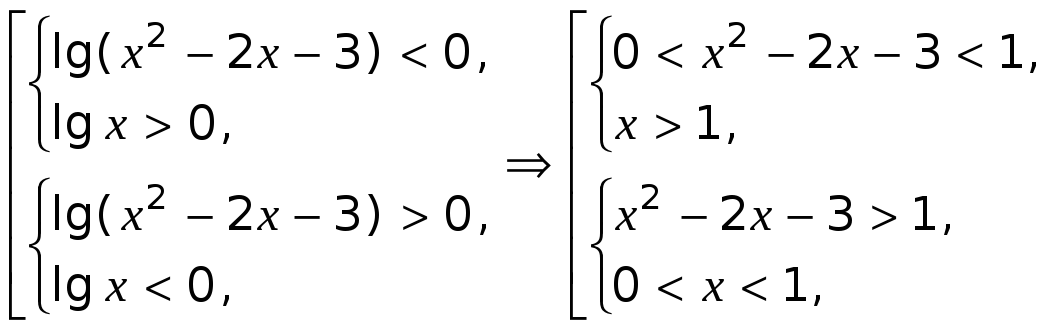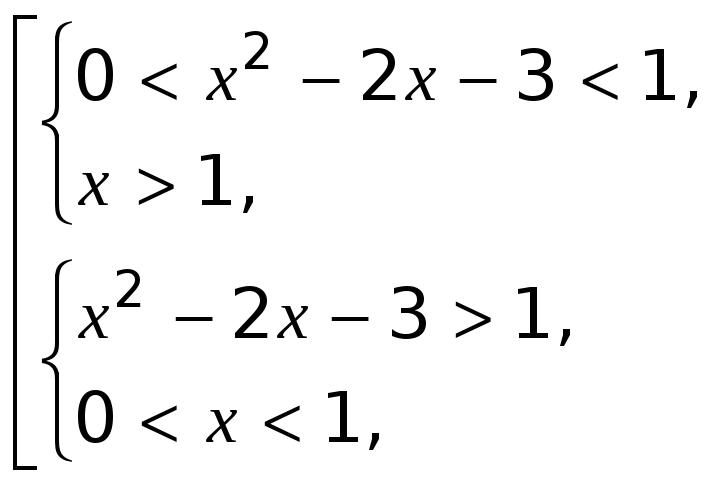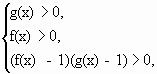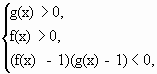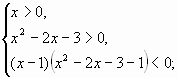Приложение 5
Тема урока: Решение логарифмических неравенств, содержащих переменную под логарифмом и в основании логарифма
Урок одного неравенства формирует навыки исследовательской работы, развивает сообразительность, повышает интерес учащихся к работе. Его лучше проводить, когда учениками усвоены необходимые понятия и разобран ряд частных приёмов решения логарифмических неравенств. На этом уроке ученики – активные участники поиска решения.
Тип урока. Урок по комплексному применению знаний и способов деятельности.
Цели урока:
Способствовать формированию навыков и умений решать логарифмических неравенств указанного типа разными способами.
Тренировать мыслительные операции: анализ, синтез, обобщение, познавательные процессы.
Развивать логическое мышление, коммуникативные способности.
Способствовать развитию самоорганизации при стремлении к достижению цели.
Ход урока.
1. Организационный момент.
Устная работа.
2. Сообщение темы урока, его целей и задач.
Анализируя варианты вступительных экзаменов по математике, можно заметить, что из теории логарифмов на экзаменах часто встречаются логарифмические неравенства, содержащие переменную под логарифмом и в основании логарифма.
Наш урок – это урок одного неравенства, содержащего переменную под логарифмом и в основании логарифма, решенного разными способами. Говорят, что лучше решить одно неравенство, но разными способами, чем несколько неравенств одним и тем же способом. Действительно, вы должны уметь проверять свои решения. Лучше проверки нет, чем решение задания другим способом и получение того же ответа (можно разными способами придти к одним и тем же системам, к одним и тем же неравенствам, уравнениям). Но не только эта цель преследуется при решении заданий разными способами. Поиски разных способов решения, рассмотрение всех возможных случаев, критическая оценка их с целью выделения наиболее рационального, красивого, является важным фактором развития математического мышления, уводят от шаблона. Поэтому сегодня мы решим только одно неравенство, но постараемся найти несколько способов для его решения.
3. Творческое применение и добывание знаний, освоение способов деятельности путем решения проблемных задач, построенных на основе ранее усвоенных знаний и умений при решении неравенства 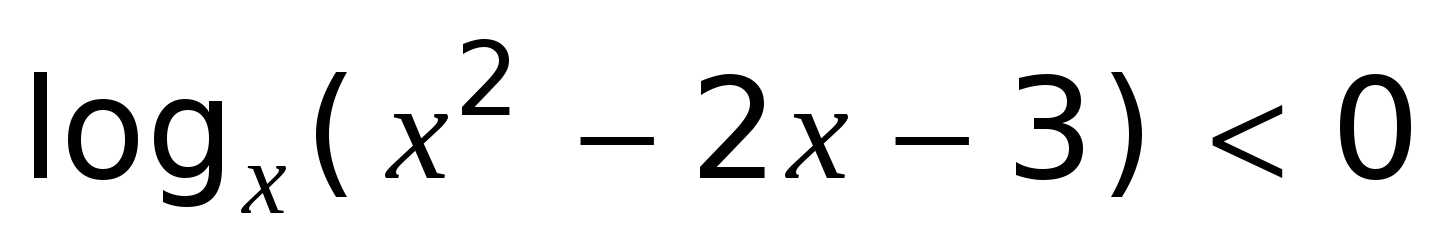
Перед вами решение этого неравенства, взятое из одной экзаменационной работы. Посмотрите внимательно на него и попробуйте проанализировать решение. (Решение неравенства записано заранее)
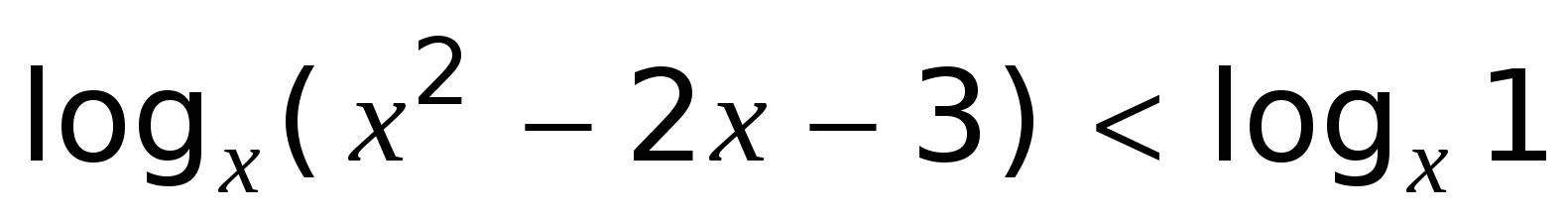
a) x2 – 2x – 3 0; (х+1)(х-3)0
б) x2 – 2x – 3 2 – 2x – 4
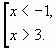
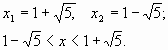
в) решение системы 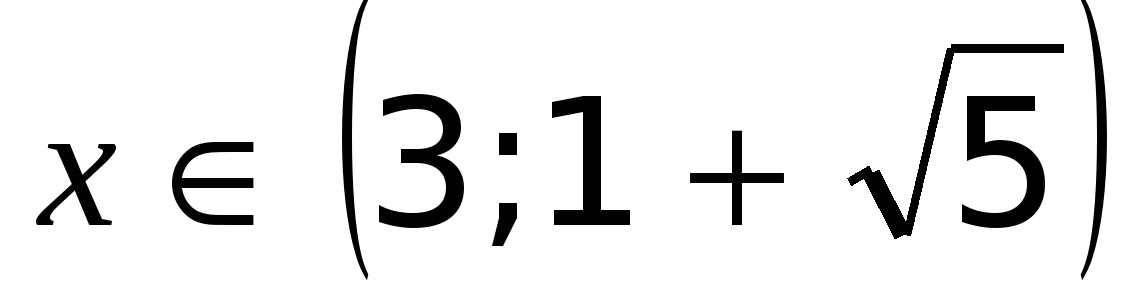 . Ответ :
. Ответ : 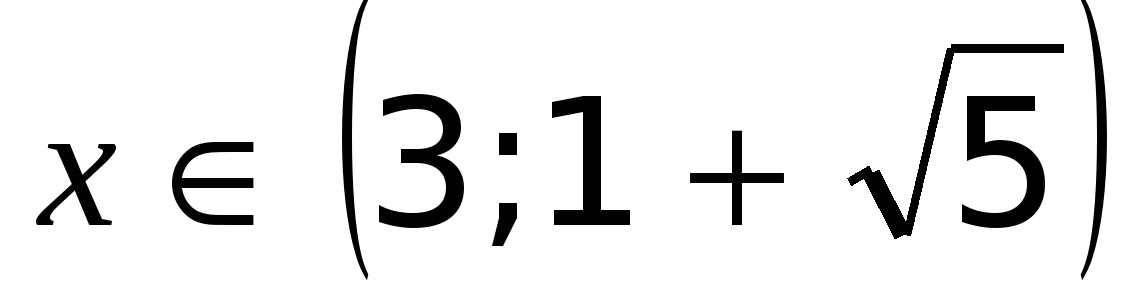
В предложенном решении неравенства был получен верный ответ Почему?
Возможные объяснения учеников:
Это не уравнение, а неравенство, поэтому при переходе от логарифмического неравенства к рациональному знак неравенства будет зависеть от основания логарифма и монотонности логарифмической функции.
При таком решении возможно приобретение посторонних решений, или потеря решений, а возможно, что при неверном решении будет получен верный ответ.
Так как же надо было решать это неравенство, в котором переменная под знаком логарифма и в основании логарифма?!
I способ.
Данное неравенство равносильно совокупности двух систем неравенств.
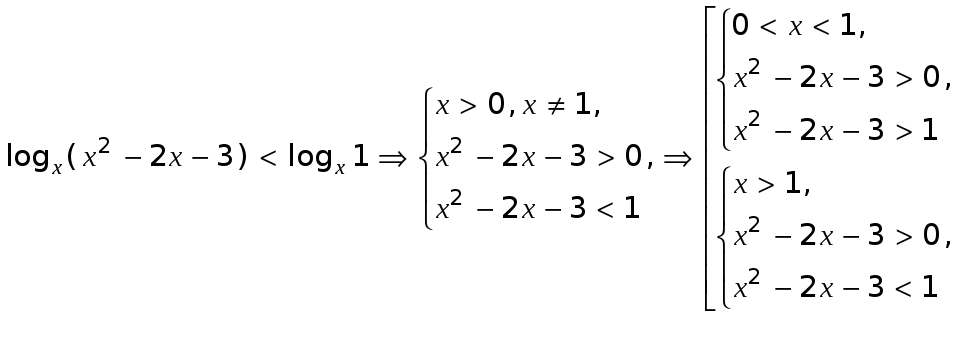
Первая система неравенств не имеет решений Решением второй системы будет интервал 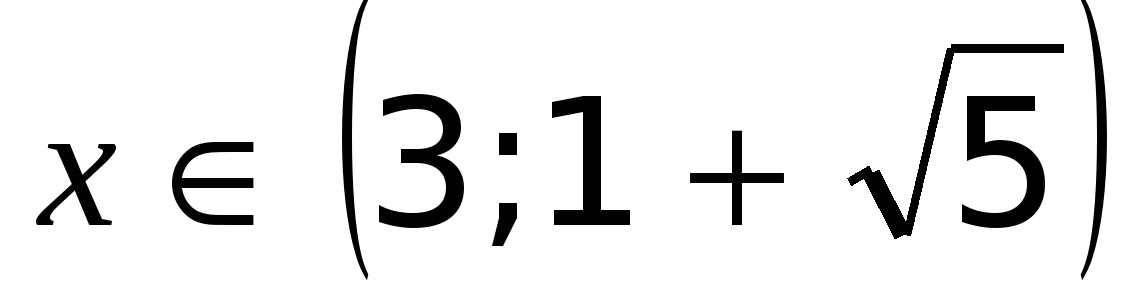 . Следовательно, решением системы неравенств будет интервал
. Следовательно, решением системы неравенств будет интервал 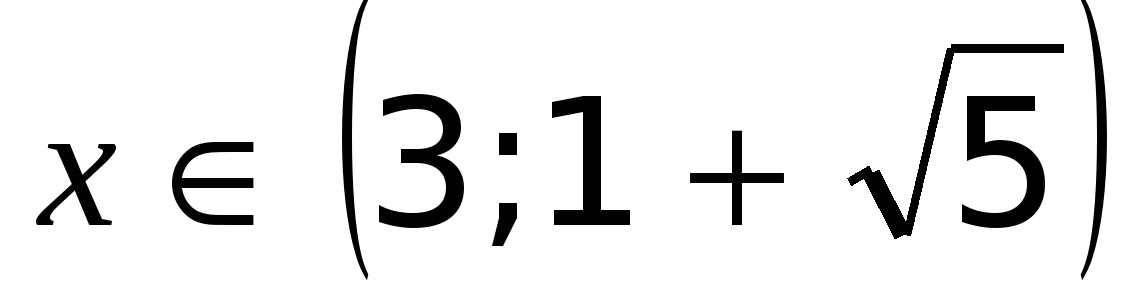
Ответ: 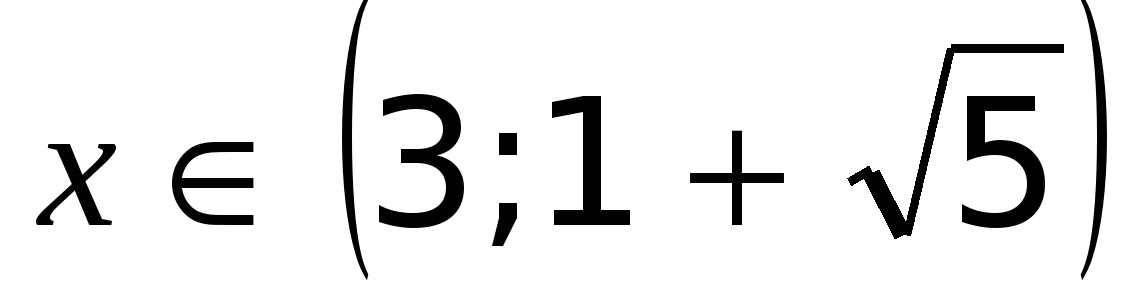
В предложенном решении неравенства из экзаменационной работы ответ был получен верный. Почему?
Возможные ответы учеников:
Так как область определения функции стоящей в левой части неравенства состоит из чисел больших 3, следовательно, функция  – возрастающая. Поэтому ответ получился верный.
– возрастающая. Поэтому ответ получился верный.
Как же можно было записать математически грамотное решение в экзаменационной работе?
II способ.
Найдём область определения функции, стоящей в левой части неравенства, а затем, учитывая область определения, рассмотрим только один случай
Как еще можно решить это неравенство? Какие формулы можно применить?
Формулу перехода к новому основанию a 0, a  1
1
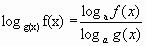
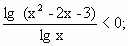
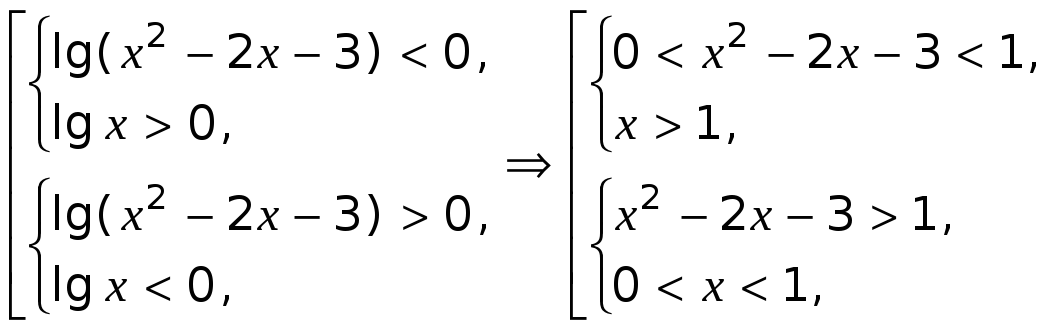
III способ.
А можно ли применить к самому неравенству то, что логарифм меньше нуля?
Да. Выражение, стоящее под логарифмом, и основание логарифма находятся по разные стороны от единицы, но положительны!
То есть, получаем опять ту же совокупность двух систем неравенств:
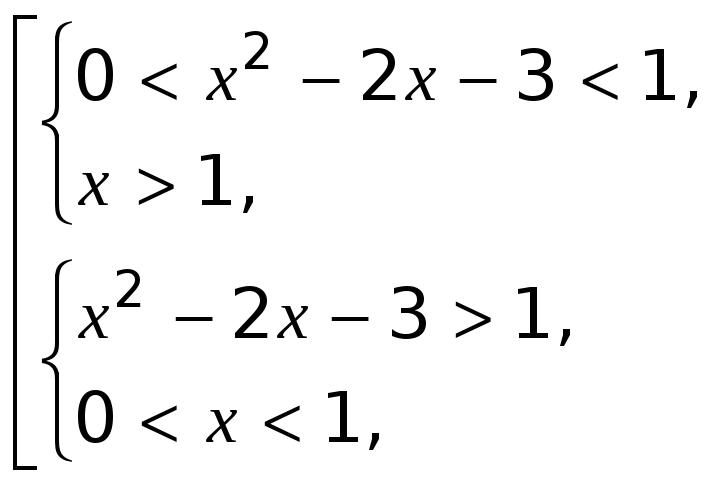
Все рассмотренные способы приводят к совокупности двух систем неравенств. Во всех случаях получается один и тот же ответ. Все способы верно теоретически обоснованы.
IV способ.
Вопрос ученикам: Как вы думаете, для чего в домашнем задании был задан вопрос, не относящийся к материалу, изучаемому в 11 классе?
Зная свойства логарифма о том, что logаblogab 0, если a и b по одну сторону от 1, можно получить очень интересный и неожиданный способ решения неравенства. Об этом способе написано в статье “Некоторые полезные логарифмические соотношения” в журнале “Квант” № 10 за 1990 год.
logg(x)f(x) 0, если
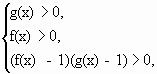
log g(x) f(x) , если
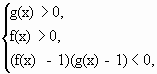
(Почему условие g(x) 1 писать не надо?)
1 писать не надо?)
Решение неравенства log x (x2 – 2x – 3) выглядит так:
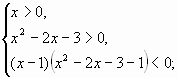
a) x2 – 2x – 3 0; б) (x – 1)(x2 – 2x – 4)


в) решение системы неравенства

V способ.
Метод интервалов. (“Решение логарифмических неравенств методом интервалов” - тема следующего урока).
4. Итог проделанной работы.
Вопросы:
1. Какими же способами было решено неравенство? Сколько способов для решения этого неравенства мы нашли? Какой из них наиболее рациональный? Красивый? На чем было основано решение неравенства в каждом случае? Чем интересно данное неравенство?
5. Обобщение изученного материала.
Нельзя ли рассмотреть это неравенство как частный случай более общей задачи?
Неравенство вида logg(x) f(x)) log g(x) h(x) можно свести к неравенству log g(x) p(x) ) 0 с помощью свойств логарифмов и свойств неравенств.
Решите неравенство logx(x2 + 3x – 3)1 любым из рассмотренных способов.
6. Домашнее задание, инструктаж по его выполнению.
1. Решите неравенства (из вариантов вступительных экзаменов по математике):logx2 (2 + x) ;  log 3x + 5 (9x2 + 8x + 8) 2;
log 3x + 5 (9x2 + 8x + 8) 2;
2. На следующем уроке будем рассматривать логарифмические неравенства, которые решаются методом интервалов. Повторить алгоритм решения неравенств методом интервалов.