Вариант 4.


Рисунок 1. Рисунок 2.
Автомобильное колесо, как правило, представляет собой металлический диск с установленной на него резиновой шиной. Диаметр диска совпадает с диаметром внутреннего отверстия в шине.
Для маркировки автомобильных шин применяется единая система обозначений. Например, 195/65 R15 (рис. 1). Первое число (число 195 в приведённом примере) обозначает ширину шины в миллиметрах (параметр B на рисунке 2). Второе число (число 65 в приведённом примере) — процентное отношение высоты боковины (параметр на рисунке 2) к ширине шины, то есть 
Последующая буква обозначает тип конструкции шины. В данном примере буква R означает, что шина радиальная, то есть нити каркаса в боковине шины расположены вдоль радиусов колеса. На всех легковых автомобилях применяются шины радиальной конструкции.
За обозначением типа конструкции шины идёт число, указывающее диаметр диска колеса d в дюймах (в одном дюйме 25,4 мм). Таким образом, общий диаметр колеса D легко найти, зная диаметр диска и высоту боковины.
Возможны дополнительные маркировки, обозначающие допустимую нагрузку на шину, сезонность использования, тип дорожного покрытия и другие параметры.
Завод производит легковые автомобили определённой модели и устанавливает на них колёса с шинами маркировки 195/60 R16.
Завод допускает установку шин с другими маркировками. В таблице показаны разрешённые размеры шин.
| Ширина шины, мм | Диаметр диска (дюймы) |
| 16 | 17 | 18 |
| 185 | 185/65 | 185/60 | - |
| 195 | 195/60 | 195/55 | - |
| 205 | 205/55; 205/60 | 205/50 | 205/45 |
| 215 | 215/55 | 215/50 | 215/40; 215/45 |
Шины какой наименьшей ширины можно устанавливать на автомобиль, если диаметр диска равен 16 дюймам? Ответ дайте в миллиметрах.
На сколько миллиметров радиус колеса с шиной маркировки 205/60 R16 больше, чем радиус колеса с шиной маркировки 185/65 R16?
На сколько миллиметров увеличится диаметр колеса, если заменить колёса, установленные на заводе, колёсами с шинами маркировки 185/60 R17?
На сколько процентов увеличится пробег автомобиля при одном обороте колеса, если заменить колёса, установленные на заводе, колёсами с шинами маркировки 195/55 R 17? Результат округлите до десятых.
Дмитрий планирует заменить зимнюю резину на летнюю на своём автомобиле. Для каждого из четырёх колёс последовательно выполняются четыре операции: снятие колеса, замена шины, балансировка колеса и установка колеса. Он выбирает между автосервисами А и Б. Затраты на дорогу и стоимость операций даны в таблице.
| Автосервис | Суммарные затраты на дорогу | Стоимость для одного колеса |
| Снятие колеса | Замена шины | Балансировка колеса | Установка колеса |
| А | 240 руб. | 54 руб. | 365 руб. | 200 руб. | 54 руб. |
| В | 438 руб. | 47 руб. | 330 руб. | 180 руб. | 47 руб. |
Сколько рублей заплатит Дмитрий за замену резины на своём автомобиле, если выберет самый дешёвый вариант?
Найдите значение выражения – 3,6 + 7,2 · 1,5.
Сравните числа x и y, если х = (27,5 ·  , у = 0,003.
, у = 0,003.
В ответ запишите значение меньшего из чисел.
Найдите значение выражения  : (2х – 2) при а = - 5.
: (2х – 2) при а = - 5.
Решите систему уравнений 
В ответе запишите х + у.
Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 0,27. Покупатель в магазине выбирает одну шариковую ручку. Найдите вероятность того, что эта ручка пишет хорошо.
Установите соответствие между графиками функций и формулами, которые их задают.
 1) у =
1) у =  2) у = 2х; 3) у = х²- 2.
2) у = 2х; 3) у = х²- 2.
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
Длину биссектрисы треугольника, проведённой к стороне a, можно вычислить по формуле  . Вычислите
. Вычислите  , если
, если  , b = 3, c = 1.
, b = 3, c = 1.
Решите систему неравенств:  На каком рисунке изображено множество её решений?
На каком рисунке изображено множество её решений?

В ходе распада радиоактивного изотопа его масса уменьшается вдвое каждые 6 минут. В начальный момент масса изотопа составляла 560 мг. Найдите массу изотопа через 30 минут. Ответ дайте в миллиграммах.
Найдите меньший угол равнобедренной трапеции, если два ее угла относятся как 2:7. Ответ дайте в градусах.
Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 74°. Найдите угол C этой трапеции. Ответ дайте в градусах.
Радиус круга равен 36, а длина ограничивающей его окружности равна 72 . Найдите площадь круга. В ответе запишите площадь, деленную на
. Найдите площадь круга. В ответе запишите площадь, деленную на  .
.
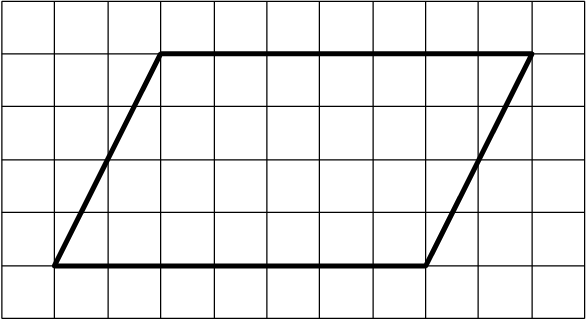
18. На клетчатой бумаге с размером клетки 1 1 изображён параллелограмм. Найдите его площадь.
1 изображён параллелограмм. Найдите его площадь.
19. Какие из следующих утверждений верны?
1) Через заданную точку плоскости можно провести только одну прямую.
2) Серединные перпендикуляры к сторонам треугольника пересекаются в точке, являющейся центром окружности, описанной около треугольника.
3) Если в параллелограмме две соседние стороны равны, то этот параллелограмм является ромбом.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
20. Сократите дробь:  .
.
21. Первые 5 часов автомобиль ехал со скоростью 60 км/ч, следующие 3 часа со скоростью 100 км/ч, а последние 4 часа со скоростью 75 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
22. Постройте график функции у =  и определите, при каких значениях k прямая у = kx имеет с графиком ровно одну общую точку.
и определите, при каких значениях k прямая у = kx имеет с графиком ровно одну общую точку.
23. В трапеции ABCD боковые стороны AB и СD равны, CH ― высота, проведенная к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 26, а меньшее основание BC равно 19.
24. Сторона CD параллелограмма ABCD вдвое больше стороны BC. Точка N – середина стороны CD. Докажите, что BN – биссектриса угла ABC.
25. Прямая, параллельная основаниям трапеции ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=54, BC=27, CF:DF=7:2.










 , у = 0,003.
, у = 0,003.  : (2х – 2) при а = - 5.
: (2х – 2) при а = - 5.
 1) у =
1) у =  2) у = 2х; 3) у = х²- 2.
2) у = 2х; 3) у = х²- 2. . Вычислите
. Вычислите  , если
, если  , b = 3, c = 1.
, b = 3, c = 1. На каком рисунке изображено множество её решений?
На каком рисунке изображено множество её решений?
 . Найдите площадь круга. В ответе запишите площадь, деленную на
. Найдите площадь круга. В ответе запишите площадь, деленную на  1 изображён параллелограмм. Найдите его площадь.
1 изображён параллелограмм. Найдите его площадь.
 .
. и определите, при каких значениях k прямая у = kx имеет с графиком ровно одну общую точку.
и определите, при каких значениях k прямая у = kx имеет с графиком ровно одну общую точку.









